《SuperPoint:Self-Supervised Interest Point Detection and Description》笔记

《SuperPoint: Self-Supervised Interest Point Detection and Description》笔记

文章解决了什么问题

通过卷积神经网络训练有监督的关键点检测模型时，对关键点概念的定义是模糊的，因此使用强监督方法训练卷积神经网络是困难的。
本文提出了一个通过自训练的自监督模型，创建了一个大的pseudo-ground truth的数据集，通过关键点检测器进行监督而非人工标注。
(a)为了生成pseudo-ground truth关键点，我们首先在几百万张合成数据集（由一些简单的几何形状及其关键点组成）中训练了一个全卷积神经网络，这个训练好的检测器称为MagicPoint，它

• 在合成数据集上表现比传统方法更好
• 尽管存在邻域适应困难，在真实图像中表现中也很好
• 但与经典的特征点检测器在各类不同的数据集上的表现相比，遗漏了一些关键点

(b)为了弥补上述的第三个问题，本文提出了一个multi-scale,multi-transform技术——Homographic Adaptation（后文简称为HA），HA是为了提高自监督关键点检测器的表现。它多次wrap输入图像来帮助特征点检测器来从多角度和尺度（scale）来理解图像。我们结合HA和MagicPoint来提高检测器的表现并生成pseudoo-ground truth关键点，得到易于可复现的和抗干扰强的检测器（称为SuperPoint）。

©最后将Superpoint与描述子子网络结合，以通过描述子得到更鲁棒和可重复的关键点检测器

综合来说，本文提出了一个自监督的框架来训练关键点检测器和适合多视角几何问题的特征描述子。

用了什么方法

自监督训练方法
使用全卷积神经网络架构，一个共享的encoder对图片进行编码，两个decoder分别检测关键点和生成描述子

效果如何

• large boost in repeatability
• outperforms classical detectors under illumination changes
• on par with classical detectors under viewpoint changes
• Homography Estimation
  • outperform LIFT and ORB
  • perform comparably to SIFT
• outperform LIFT in almost all metrics quantitatively
• scores strongly in descriptor-focused metrics such as NN mAP and M.score, which means learned representations for descriptor matching outperform hand-tuned representations.

结论

• 将合成数据集的知识迁移到真实图像上是可能的
• 稀疏的关键点检测和描述可以由简单高效的卷积神经网络来解决
• 整个系统在集合计算机视觉匹配任务上表现很好

存在什么不足

Future Work

• 为何Homographic Adaption可以提高模型的表现
• 关键点检测和特征描述生成是如何相辅相成的
• 研究HA是否能提高一些语义分割和目标检测模型的表现

细节

过程

整个过程如图所示

构建合成数据集

• 构建如图的合成数据集，合成形状是由简单的2D图形（四边形、三角形、线、椭圆）组成的，定义的关键点位置为Y结、L结、T结、小椭圆的中心和线段分割处，注意这样给出的关键点实际是真实关键点的子集，但是模型最终的效果依然很好
• 对上一步结果进行Homographic wrap来进行数据增强

训练MagicPoint

在合成数据集上训练MagicPoint，验证其效果优于一些经典算法

MagicPoint + Homographic Adaption生成pseudo ground truth

这一步使用训练好的MagicPoint来为目标领域图像进行pseudo ground truth生成

核心是使用随机的homography（如图）来wrap输入图像，并结合同源图像的输出图像，随机的homography是由简单的变换复合而成，这个过程就是Homographic Adaption

对于关键点检测函数$f_{\theta }$（即MagicPoint），记$I$为输入图像，$x$为输出关键点，$H$为随机Homography，则有
$$x=f_{\theta }(I)$$
$H$与$f_{\theta }$可交换，则有
$$Hx=f_{\theta }(H(I))$$

$$x=H^{-1}(f_{\theta }(H(I)))$$
通过足够多的随机的$H$，来提升关键点检测器的性能，最终的检测器为
$$\hat{F}(I;f_{\theta })=\frac{1}{N_h}\sum _{i=1}^{N_h}{H}_i^{-1}(f_{\theta }(H_i(I)))$$

选择Homography（3×3矩阵）

并非所有Homography都是适合的，首先从截断正态分布中采样各种基变换，然后结合为一个Homography

SuperPoint

最后pseudo ground truth被用来训练SuperPoint，这个过程就是普通的监督模型

超参数$N_h$的选择

默认第一个Homography为恒等变换，因此$N_h=1$默认为没有进行变换，合适的值为$N_h=100$

网络结构

MagicPoint架构

MagicPoint实际上就是SuperPoint没有生成descriptor那部分的结构

Encoder架构

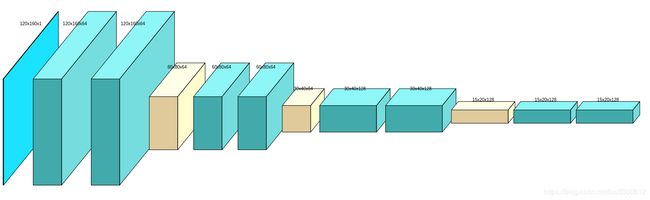
input(120, 160, 1)
conv(120, 160,64)
conv(120, 160,64)
pool(60, 80, 64)

conv(60, 80,64)
conv(60, 80,64)
pool(30, 40, 64)

conv(30, 40,128)
conv(30, 40,128)
pool(15, 20, 128)

conv(15, 20, 128)
conv(15, 20, 128)

为了显示全图，省略了relu操作，relu就是stride为2，kernel_size为2的常规非线性操作

Detector Head架构

输出是一个(15,20,65)的tensor，除去最后一维“no interest dustbin”之后，剩余的(15,20,64)的结果可以reshape成原图的大小(120,160)
Detector Head对Encoder得到的feature进行decode，通过增加深度，最后将深度重新reshape到长宽维上实现与原图一样大小的输出，这里之所以不使用upconvolution的原因是add a high amount of computation and can introduce unwanted checkerboard artifacts[18]

损失函数

关键点检测损失函数

$$L_p(X,Y)=\frac{1}{H_c{W}_c}\sum _{h=1,w=1}^{H_c,W_c}{l}_p({\mathbf{x}}_{hw};y_{hw})$$
其中，$H_c=H/8,W_c=W/8$，且
$$l_p({\mathbf{x}}_{hw};y)=-\log \frac{\exp ({\mathbf{x}}_{hwy})}{{\sum }_{k=1}^{65}\exp ({\mathbf{x}}_{hwk})}$$
注意到detector的输出是(15,20,65)的，除去最后一个深度维后，剩下(15,20,64)对应着原图（120,160）的15*24个8*8的区域，对每个这样的区域，关键点所在的第几个位置（将8/*8的区域拉成64维向量）即是$y_{hw}$的值，若区域中没有关键点，则$y_{hw}=65$，显然，从上面的损失函数中，默认了每个8*8区域中只有一个关键点，如果某个区域中有多于1个的关键点，则会在其中随机选择一个，虽然网络训练时使用随机的关键点，但是，实际的时候，大于最低置信度的点都会被认为是关键点，在训练过程中，只要多个关键点都多次被选中，可能可以检测出所有关键点。

术语

• SLAM(Simultaneous Localization and Mapping)，同步定位与建图，机器人在未知环境中从一个未知位置开始移动,在移动过程中根据位置估计和地图进行自身定位，同时在自身定位的基础上建造增量式地图，实现机器人的自主定位和导航
• SfM(Structure-from-Motion)，运动恢复结构，在计算机视觉指的是，通过分析物体的运动得到三维结构信息的过程。
• semantic segmentation
• 全卷积，将传统的卷积神经网络最后几层全连接网络也换成卷积层的神经网络
• corresponding points，不同视角看到的物理位置相同的点
• Homography，是一个映射，将一幅图像中的点映射到另一幅图像中的corresponding point
• truncated normal distribution，截断正态分布，限制服从正态分布随机变量的取值范围

复现

在Superpoint中找到的Synthetic dataset的生成方法

生成数据集

生成的数据集有9类，分别是

类别	每张图的图形个数	备注
checkerboard	1
cube	1
ellipse	多	没有关键点
line	多
multiple polygon	多
polygon	1	多为三角形
star	1	实际不是星星，是线段交成的结形
stripes	多
gaussian noise	?	噪声

其中，每类包含训练集10000，测试集500，验证集200，总计训练集90000，测试集4500，验证集1800
样本如下图

遇到的问题

Ground Truth 和 Label的关系

前文的损失函数中有写明

样本不均衡问题

并没有特别的解决样本不均衡问题的方法，作者在pretrained model中设置了检测最低置信度为0.015（约为1/65），而tf实现中，检测的最低置信度更是0.001

网络debug

由于实际训练时，用上述的置信度，得出的网络输出的兴趣点都分布在如图的边缘，所以可能需要debug网络

使用单张图片放入网络训练

1.训练出的网络对输入不敏感，且输出的热力图的8*8网格中每个小格子输出一样


几乎差不多的热力图，网络的输出损失也很大，预测结果和全部热力图如下图，这是欠拟合的表现

2.增大训练轮次后输出scale不同
损失小于1e-5，但预测时出现指数溢出，查看输出，发现15*20的每个65维输出的scale不一样，有的是0~80，有的是-40~0，统计结果如下

位于output[1,:,:]的统计结果

位于output[59,:,:]的统计结果

所以求exp的时候会溢出，loss的数值也不稳定，此时对每个15*20的channel求argmax时，得到的结果已经和label完全一致，可能是过拟合的表现，且在训练过程中，loss瞬间从0.5下降到0.002，可能是momentum在同一张图片上训练更新向量累积模太大，所以去掉momentum，且为防止过拟合，设定最小loss阈值

注意因为此处label一致，我曾想通过归一化来保证预测时exp的数值稳定，但实际上是不可行的，因为不能做统一的归一化，这样会导致scale相对小的激活值输出的置信度很低，也不能做15*20区域中每个64维向量分别的归一化（？但是softmax的时候实际上是这样做的），这样会导致每个区域都有较大的激活值

• 可能是因为输入没处理好的原因
• 可能是标签没处理好的原因
• 可能是输出转化到标签没处理好的原因
• 可能是loss函数不对的原因
• 框之间的大小不可比？？？尽管是框中最大的激活值，还没有别的框中的非关键点激活值大？

计算了下损失的上界
-log(1/65) = 4.1744

找到问题

通过以下三个步骤后，问题最终解决

• 加上batch normalization层，loss从0.28~0.30降低到0.16~0.2
• 加上learning rate decay后，loss从0.16~0.2降低到0.13以下
• 更换优化器为Adam后，训练误差降低到0.002以下

所以最终问题主要是因为更换了Adam优化器而解决，原来的网络存在优化上的问题而不是复杂度不足的问题时，也会出现train loss和test loss都很大的情况，即便尝试了多种SGD的learning rate也无法彻底解决

MagicPoint 训练结果

训练过程可视化

使用tf版本的参数，在90000张数据集上训练了90个epoch，并在每个epoch计算模型在测试集上的误差（此处的误差图像有误，训练误差忘记除以1000，测试误差忘记除以4500），最后模型在第17轮的误差最小，为0.03682，训练误差为0.011602，由于分了两次训练所以途中的曲线是两个不同的颜色

在训练集和测试集上的表现

左红色是ground truth，右蓝色是预测结果，这里使用了github上pretrained model的网络前端，对预测结果执行盒半径为4的nms并消除边缘上的一些预测结果，得到以下结果

训练集

测试集

evaluation

测试的时候发现即便在图中看起来MagicPoint的预测结果与ground truth相似，但是实际的准确率和召回率均很低，调整好阈值之后，均在0.6左右，加上nms之后，可以达到0.8左右

奇怪的现象，即便test_loss变大了，但是precision和recall竟然也变大

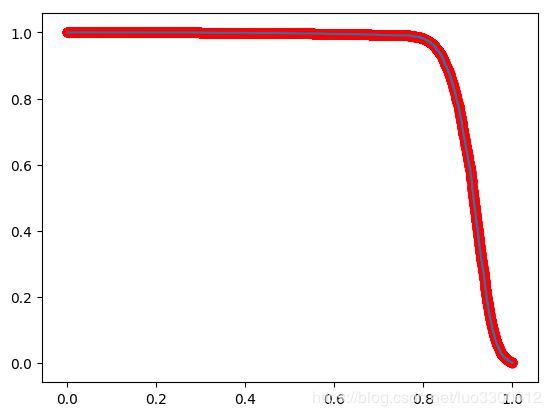
计算mAP

为了计算出mAP，先要计算出AP值，这里遇到了以下误区：

• 计算每张图片的AP然后加和平均：这种算法是错的，而且对于全是高斯噪声的图片，由于全是负类标签，所以计算准确率和召回率的时候会出现分母为0的情况
• 为了弥补第一步中的错误，应该在全数据集上直接计算AP，因为作者评估的时候选择了1000张图片，所以计算AP的时候需要维持几个1000*120*160的数组，这对内存是很大的开销，直接计算得到AP仅有0.56，这是因为没有使用$ϵ=4$的容错率，即对于在关键点周围四格以内的预测均计算为正确的

由于作者没有给出细节，而在普通的计算AP的算法上加上$ϵ=4$的容错是十分奇怪的做法，因为当预测值不是标签但小于容错的时候，既不能直接将其计算为TP，因为这样做会导致recall最后大于1，也不能动态改变recall的分母，因为这会影响AP中给定r计算最大p的过程，更不可以将其算作FP，因为这样会导致precision偏低，我的选择是，当发现某个label周围$ϵ=4$中的第一个点时，即给TP加一，之后该区域中出现的所有点都不再算如TP中，这样做既能保证第一时间将检测到的点加入TP，同时保证了给定r计算最大p的正确性

针对前两个错误，提出第三个计算AP的方法：

Created with Raphaël 2.2.0 初始化预测为正例的样本数K为0，所有样例预测值全为0，TP=0，真实标签为1的样本数记为N K<预测样例数 选择激活最大的一个样本s，K=K+1 s是正确label周围四格以内的点 正确label位置的预测值是否被标记为1 K=K-1，即直接跳过本次的样例加入，因为之后不会再看到该样例，这样做等价于将该样例的激活值设为0 结束 将正确label的预测值标记为1，TP=TP+1 计算precision=TP/K , r=TP/N yes no yes no yes no

这样计算出的AP是0.8034，pr曲线如图，红点标注的是固定r可以达到的最大p的位置

疑惑：大致观察了样本上的预测效果，几乎都在90%准确和召回率，为什么总体的AP这么低？相对于论文上的mAP=0.979，即便我计算出负类的AP是1，总的AP也只有0.9左右

分类计算AP和pr曲线：
1.checkerboard
AP=0.9518

2.cube
AP=0.9687

3.ellipse
undefined
4.line
AP=0.9387

5.multipoly
AP=0.9060

6.poly
AP=0.9536
W
7.star
AP=0.9739

8.stride
AP=0.5030

9.noise
undefined

可见，模型在stride上的预测效果非常差，对此去掉几大类后重新评估：

• 去掉stride AP=0.82
• 去掉stride和noise AP=0.87
• 去掉stride和noise和ellipse AP=0.91

由于严重的样本不均衡问题，负类的AP几乎可以估计为1，则去掉三类后的mAP=(0.91+1)/2=0.955，接近论文给出的值，但由于论文没有详细给出evaluation的方法，上述算法只是我根据给出的一个直观的评估方法，因此会有差异，但总体看来，除了在一些负样本上，模型的效果已经不错

Homography（单适应变换）

论文中提到的Homography是从简单变换采样复合而成的，简单变换包括

• root center crop（以目标为中心的crop）
• translation（平移）
• scale （缩放）
• in-plane rotation（旋转），详解，1
  • In Plane Rotation: Suppose you have a camera that is looking on an object and imagine a vector starting from the center of the camera lens and going to the object. Now if you simply spin your camera along that vector this is called in plane rotation (the plane of your camera lens does not change but it has rotated in this plane). The image of the object after this rotation only shows that object has rotated nothing else changes.
  • Out of plane rotation: any other rotation where the new position of the camera lens is not in its last plane.
• symmetric perspective distort

添加homograpy后的检测结果

Nh=1，即没有homography

Nh=10

Nh=100

显然增加Nh之后可以检测到更多的关键点，现在问题是，Nh增加对边界附近点的检测提升度不高，这主要是因为目前使用的Homography均不允许超越边界的原因，因此采样被集中到了图片中间区域，这一点可以通过采样热力图展示出来

homography偏向左上角部分

修改参数，发现这是因为wrap参数设置不当造成的，因为center crop的比例是0.5，合理的我将图片通过perspective变换到它们一半尺寸的大小，结果造成图像向左上角偏，可能是因为warp回来的时候没有做一些必要的处理导致回来后坐标变小，现在可以采样的措施有：

• wrap成原来大小，让net检测
• wrap成一半大小，warp回来的时候先恢复大小再wrap

发现是findHomography时候参数错了，pts1应该是0.5倍的长宽

此时采样在分布对称了，接下来要做的就是允许超过边界的采样，然后看看magic point 在hpatches上的表现

问题

• full-sized image什么意思
• 合成数据集具体如何生成
• Intro的最后一段，robust and repeatable interest points中的repeatable是什么意思
• MagicPoint的架构是怎样的
• SuperPoint的descriptor decoder的label哪里来的
• 当一个bin（8*8区域）中有多于1个关键点的时候，是该图片每次进入网络后随机选一个关键点，还是一开始生成label的时候随机选一个关键点：在tensorflow的实现中，直接使用argmax操作找到位置，这使得生成label时自动找靠前的位置的关键点作为关键点
• 在label和point相互转化的时候采取向下取整，损失了一些精度
• 直接使用原始的损失函数，训练过程中，loss一直下降，但sample出来的图片上没有关键点，且每次output除去dustbin后的最大输出值越来越低（即最可能是关键点的位置的置信度），因为每张图片大约有0-10左右个关键点，而其余上千上万个点都不是关键点，因此正负样本的比例悬殊，导致了这一问题
• 验证集是否就是CS231n里所说的在小训练集上训练看看能否过拟合，同时也可以调超参数？
• adam的公式是什么

Reference

• Superpoint，基于tensorflow的SuperPoint
• SuperpointPretrainedNetwork，
  作者预训练的SuperPoint模型，可以调用到图片、视频和摄像头上，但作者明确说明不会开放训练代码、合成数据集
• demoasd ,youtube上的视频Demo，在高分辨率的情况下似乎有很大的问题
• 关于损失函数