CVPR2018 SPG、KCNet、PointwiseCNN

嘤嘤嘤，SPG还没搞懂但是实验效果不错，KCNet，Pointwise都是从类似于卷积核提取特征的切入点入手的。

CVPR2018 SPG

Large-scale Point Cloud Semantic Segmentation with Superpoint Graphs
（论文链接）（pytorch源码链接）
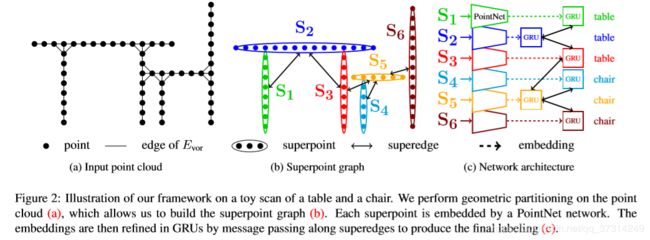
不同于此前的工作，SPG不是去逐点进行分类，而是将多个点组成的点集看作一个完整的整体，对每个点集再进行分类，并且可以描述相邻物体之间的关系，非常适用于上下文分类。SPG的大小是由场景中简单结构的数量来确定的，而不是点的总数。
(啊。好复杂啊。里边好多东西都不太懂，之前没了解过，提到的一些论文也需要看一下。以后慢慢填吧这个坑。但是从最后实验的结果来看，效果确实不错。)

Problem & Solution

Geometrically homogeneous partition 将点云划分为简单的几何图形，suprerpoint
Superpoint embedding 降采样
Contextual segmentation 基于图卷积的深度学习算法

Geometric Partition with a Global Energy

进行划分的目标不是把整个物体划分出来，而是划分成多个简单的几何形体。
对于含有$n$个点的三维点云$\mathcal{C}$，每个点包括位置信息$p_i$、观测信息$o_i$(如颜色、强度等)
对于每个点，计算一组$d_g$几何特征$f_i\in {\mathbb{R}}^{d_g}$来刻画其局部邻域的形状。使用的特征包括[1]提出的线性度、平面度和散射度，垂直度特征，此外还计算了每个点的绝对高度作为点$p_i$的$z$坐标。
[1]提出的全局能量是根据点云的10个最近邻邻接图$G_{nn}=(C，E_{nn})$来定义的。几何形体划分可以被定义为下列连通分量的优化问题：
$$\arg \underset{g\in {\mathbb{R}}^{d_g}}{\min }\sum _{i\in \mathcal{C}}||g_i-f_i|{|}^2+\mu \sum _{(i,j)\in E_{nn}}{w}_{i,j}[g_i-g_j\ne 0]$$
其中$[\cdot ]$为艾佛森括号，边的权值$w\in R_{+}^{|E|}$与边缘长度成线性递减关系，$\mu$是正则化强度。
使用[2]所提出的$l_0-cut$算法快速迭代求得近似解。从上式解得的连通分量$S=S_1，\cdot \cdot \cdot ，S_k$称为superpoints。

Superpoint Graph Construction

SPG是点云的结构化表示，是一个有向图$\mathcal{G}=(\mathcal{S},\mathcal{E},F)$，节点$\mathcal{S}$是superpoints集，边$\mathcal{E}$是superpoint之间的边superedges，superedges有由特征$d_f$表示的邻接关系$F\in {\mathbb{R}}^{\mathcal{E}\times d_f}$。
定义一个[3]提出的对称Voronoi邻接图$G_{v}or=(C,E_{vor})$。如果superpoints$S$和$T$之间至少有一条边在$E_{vor}$中，那么$S$和$T$就是邻接的：
$$\mathcal{E}=\{(S,T)\in {\mathcal{S}}^2|\exists (i,j)\in E_{vor}\cap (S\times T)\}$$
与superpoints$(S，T)$相关的重要空间特征是从$E_{vor}$中的边的偏移$\delta (S,T)$获得的:
$$\delta (S,T)=\{(p_i,p_j)|(i,j)\in E_{vor}\cap (S\times T)\}$$
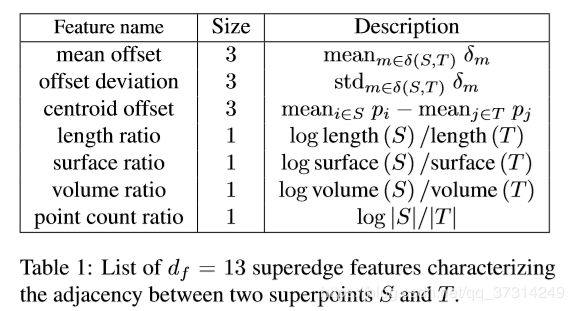
superedgs的特征也可以通过比较相邻superpoints的形状和大小来得到。其他的一些superedgs特征↓：

Superpoint Embedding

这一步的目的是将每一个superpoint$S_i$embedding得到一个$d_z$维的向量$z_i$。论文中选用了pointnet来实现。

Contextual Segmentation

受到GatedGNN和ECC的启发，首先用上一步中得到的$z_i$来初始化GRU的隐藏单元，然后迭代更新$t=1,...T$。对于每一次迭代，一个GRU的隐藏状态用$h_i^{(t)}$表示，传来的输入信息为$m_i^{(t)}$，计算得到的新的状态为$h_i^{(t+1)}$。输入$m_i^{(t)}$是相邻superpoints $j$的隐藏状态$h_j^{(t)}$的加权和，权重由 superedge$(j,i)$的特征$F_{j,i}$决定。上述计算是通过多层感知机实现，计算过程如下：
$$\begin{array}{r}{\mathbf{h}}_i^{(t+1)}=\left(1-{\mathbf{u}}_i^{(t)}\right)\odot {\mathbf{q}}_i^{(t)}+{\mathbf{u}}_i^{(t)}\odot {\mathbf{h}}_i^{(t)}\\ {\mathbf{q}}_i^{(t)}=\tanh \left({\mathbf{x}}_{1,i}^{(t)}+{\mathbf{r}}_i^{(t)}\odot {\mathbf{h}}_{1,i}^{(t)}\right)\\ {\mathbf{u}}_i^{(t)}=\sigma \left({\mathbf{x}}_{2,i}^{(t)}+{\mathbf{h}}_{2,i}^{(t)}\right),{\mathbf{r}}_i^{(t)}=\sigma \left({\mathbf{x}}_{3,i}^{(t)}+{\mathbf{h}}_{3,i}^{(t)}\right)\\ {\left({\mathbf{h}}_{1,i}^{(t)},{\mathbf{h}}_{2,i}^{(t)},{\mathbf{h}}_{3,i}^{(t)}\right)}^T=\rho \left(W_h{\mathbf{h}}_i^{(t)}+b_h\right)\\ {\left({\mathbf{x}}_{1,i}^{(t)},{\mathbf{x}}_{2,i}^{(t)},{\mathbf{x}}_{3,i}^{(t)}\right)}^T=\rho \left(W_x{\mathbf{x}}_i^{(t)}+b_x\right)\\ {\mathbf{x}}_{1,i}^{(t)}=\sigma \left(W_g{\mathbf{h}}_i^{(t)}+b_g\right)\odot m_i^{(t)}\\ m_i^{(t)}=mea{n}_{j|(j,i)\in \mathcal{E}}\left(F_{ji,.};W_e\right)\odot {\mathbf{h}}_j^{(t)}\\ {\mathbf{h}}_i^{(1)}={\mathbf{z}}_i,{\mathbf{y}}_i=W_o{\left({\mathbf{h}}_i^{(1)},\dots ,{\mathbf{h}}_i^{(T+1)}\right)}^T\end{array}$$
Input Gating
Edge-Conditioned Convolution
State Concatenation
Relation to CRFs


[1] S. Guinard and L. Landrieu. Weakly supervised segmentation-aided classification of urban scenes from 3d LiDAR point clouds. In ISPRS 2017, 2017. 2, 3, 8
[2] L. Landrieu and G. Obozinski. Cut pursuit: Fast algorithms to learn piecewise constant functions on general weighted graphs. SIAM Journal on Imaging Sciences, 10(4):1724– 1766, 2017. 3
[3] J. W. Jaromczyk and G. T. Toussaint. Relative neighborhood graphs and their relatives. Proceedings of the IEEE, 80(9):1502–1517, 1992. 4

CVPR2018 KCNet

Mining Point Cloud Local Structures by Kernel Correlation and Graph Pooling
(论文链接)(caffe源码链接)(pytorch源码链接)
PointNet++通过牺牲速度构建更加复杂的模型来更好的提取局部特征，KCNet尝试在保持网络简单结构的条件下，探寻其他有效的、可学习的、具有清晰几何解释的局部特征提取方法来改进PointNet。提出的改进主要有两个：一个是用于提取局部几何结构的kernel correlation layer，另一个是用于提高网络鲁棒性的graph-based pooling layer
最大的创新点大概在设计了kernel correlation，使得能够更好的提取点云的局部结构特征，暂时还没有看过三维卷积核直接应用到点云的网络，不知道能不能得到类似的局部特征，但是考虑到点云的数量特征，直接用三维卷积核大概是不行吧hhhh。。。。

Architecture

Learning on Local Geometric Structure

kernel points 类似于卷积核，通过反向传播来不断地调整找到一组点的参考/模板。
使用类似于Leave-one-out Kernel Correlation (LOO-KC)和 multiply-linked registration损失函数来提取局部几何结构特征。
一个可以学习$M$个点的point-set kernel $\mathbf{\kappa }$和含有$N$个点的点云的 anchor point ${\mathbf{x}}_i$ 之间核相关关系 kernel correlation(KC)如下:
$$\mathrm{K}\mathrm{C}\left(\mathbf{\kappa },{\mathbf{x}}_i\right)=\frac{1}{|\mathcal{N}(i)|}\sum _{m=1}^M\sum _{n\in \mathcal{N}(i)}{\mathrm{K}}_{\sigma }\left({\mathbf{\kappa }}_m,{\mathbf{x}}_n-{\mathbf{x}}_i\right)$$
其中${\mathbf{\kappa }}_m$是核中的第$m$个可学习点，$\mathcal{N}(i)$是anchor point ${\mathbf{x}}_i$ 的邻点的集合，${\mathbf{x}}_n$是${\mathbf{x}}_i$的邻点之一。${\mathrm{K}}_{\sigma }(\cdot ，\cdot )$：${\Re }^D\times {\Re }^D\to \Re$是任何有效的核函数（$D$是核函数维度）。为了有效地存储点的局部邻域，我们将每个点看作一个顶点来预先计算KNNG，边只连接附近的顶点。论文中选用的是高斯核函数：
$${\mathrm{K}}_{\sigma }(\mathbf{k},\mathbf{\delta })=\exp \left(-\frac{\Vert \mathbf{k}-\mathbf{\delta }{\Vert }^2}{2{\sigma }^2}\right)$$
其中，$||\cdot ||$是欧氏距离，$\sigma$是核的宽度。$\sigma$的大小对最后的结果的影响如下表：

在进行反向传播时：
$$\frac{\partial \mathcal{L}}{\partial {\kappa }_m}=\sum _{i=1}^N{\alpha }_i{d}_i\left[\sum _{n\in \mathcal{N}(i)}{\mathbf{v}}_{m,i,n}\exp \left(-\frac{{\Vert {\mathbf{v}}_{m,i,n}\Vert }^2}{2{\sigma }^2}\right)\right]$$
其中，$\mathcal{L}$是损失函数，每个点${\mathbf{x}}_i$的KC反馈$d_i=\frac{\partial \mathcal{L}}{\partial KC(\kappa ,{\mathbf{x}}_i)}$，正则常数${\alpha }_i=\frac{-1}{|\mathcal{N}(i)|{\sigma }^2}$，局部差分向量${\mathbf{v}}_{m,i,n}={\kappa }_m+{\mathbf{x}}_i-{\mathbf{x}}_n$
KC与LOO-KC的不同在于：KC计算的是相邻点和核内可学习到的点的相似性，且KC允许核中的点自由移动。
通过学习得到的

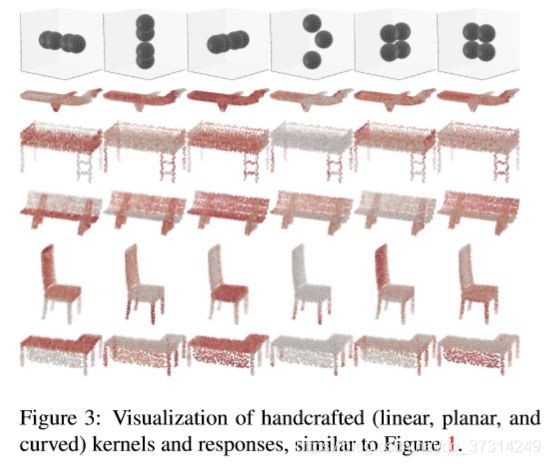
Learning on Local Feature Structure

把每个点看作顶点，只与相邻的点用边连接构造了一个KNNG。 作者认为，相邻的点趋向于拥有相似的几何结构。通过neighborhood graph的学习可以更好的提取局部特征。
graph pooling layer的输入为$\mathbf{X}\in {\Re }^{N\times K}$，KNNG的邻接矩阵$W\in R{e}^{N\times N}$，如果$i$，$j$之间有边，则$W(i,j)=1$，否则为0。通过graph pooling操作聚合其邻域内每个点的特征：
$$\mathbf{P}={\mathbf{D}}^{-1}\mathbf{W}$$
其中，$D\in {\Re }^{N\times N}$是degree matrix：$d_{i,j}=\{\begin{array}{ll}\mathrm{deg}(i),& \text{ if }i=j\\ 0,& \text{ otherwise }\end{array}$
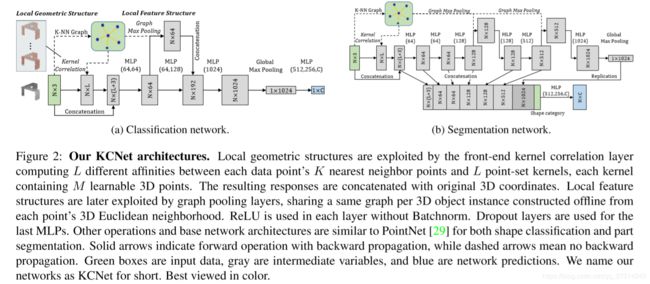
得到上述局部特征后使用graph max pooling或者average pooling，然后使用与pointnet类似的网络结构来实现分类和语义分割，具体的网络结构如Figure2.
experiment on ShapeNet part segmentation

CVPR2018 PointwiseCNN

Pointwise Convolutional Neural Networks
（论文链接）（tensorflow源码链接）
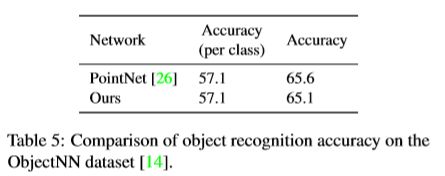
与KCNet一样，PointwiseCNN也将关注点放在了卷积算子上，提出了一种新的卷积算子，PointwiseCNN的整个网络非常的简单，点云数据集也不需要特别复杂的预处理，最后也可以在S3DIS、SceneNN、ObjectNN等数据集上得到与PointNet相差不大的准确度。

Pointwise Architecture

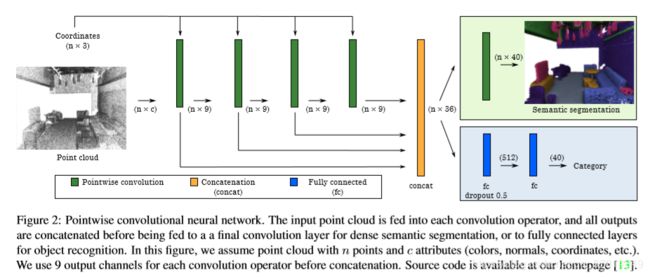
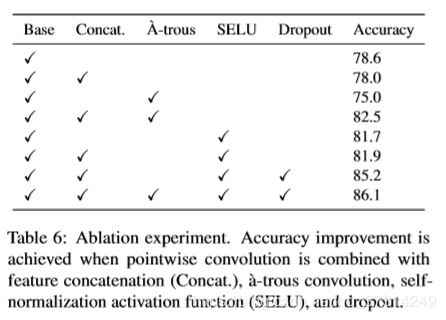
网络的结构非常的简单，使用了四层大小一致的带有Pointwise卷积操作的Pointwise Convolution Layer，将各层的输出concat到一起，然后使用一层Pointwise Convolution Layer进行语义分割，或者使用两层全连接层进行分类。

Pointwise Convolution

Convolution Pointwise Convolution卷积核的设计非常的简单，以输入点云中的某一点为中心，卷积核中的点都会对中心点有一定的贡献（卷积核的形状可以是任意的，但有大小和半径属性），如下图：

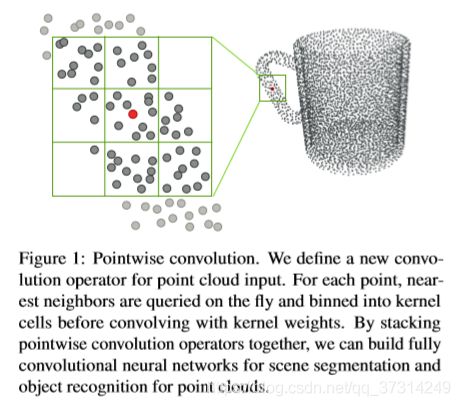
pointwise convolution 可以用下式表示：
$$x_i^{\ell }=\sum _k{w}_k\frac{1}{\left|{\Omega }_i(k)\right|}\sum _{p_j\in {\Omega }_i(k)}{x}_j^{\ell -1}$$
其中，$k$迭代所有pointwise核的子区域，${\Omega }_i(k)$是以$i$为中心的核的第$k$个子区域，$p_i$是点$i$的坐标，$|\cdot |$是对子区域中所有的点进行计数，$w_k$是核中第$k$个子区域的权重，$x_i$和$x_j$是点$i$和$j$的值，$l-1$和$l$是输入和输出层的标号。
Gradient back propagation 要进行训练就需要计算梯度来核的优化，定义损失函数为$L$，对输入的梯度可以定义为：
$$\frac{\partial L}{\partial x_j^{\ell -1}}=\sum _{i\in {\Omega }_j}\frac{\partial L}{\partial x_i^{\ell }}\frac{\partial x_i^{\ell }}{\partial x_j^{\ell -1}}$$
其中，$\frac{\partial L}{\partial x_j^{\ell }}$是在$l$层的梯度，在反向传播的过程中可以计算得到，$\frac{\partial x_i^{\ell }}{\partial x_j^{\ell -1}}$如下：
$$\frac{\partial x_i^{\ell }}{\partial x_j^{\ell -1}}=\sum _k{w}_k\frac{1}{\left|{\Omega }_i(k)\right|}\sum _{p_j\in {\Omega }_i(k)}1$$
类似的可以定义对核中权重的梯度：
$$\frac{\partial L}{\partial w_k}=\sum _i\frac{\partial L}{\partial x_i^{\ell }}\frac{\partial x_i^{\ell }}{\partial w_k}$$
其中，$\frac{\partial x_i^{\ell }}{\partial w_k}=\frac{1}{|{\Omega }_i(k)|}{\sum }_{p_j\in {\Omega }_i(k)}{x}_j^{\ell -1}$
论文中使用的核为$3\times 3\times 3$的卷积核，卷积核中所有单元的权重都是一样的。
文的网络中没有使用池化层。
Point order 作者认为输入点云是需要进行排序的，因此在输入之前，按照特定的顺序（如XYZ、Mortoncurve）对点云进行了排序。但作者认为在进行语义分割时点序是没有影响的。
A-trous convolution 很容易实现atrous convolution
Point attributes 可以添加一些颜色什么的数据进去
Relevance to geometric deep learning

一些实验结果：