Android自定义系列——9.Path详细用法
rXxx方法
rXxx方法的坐标使用的是相对位置(基于当前点的位移),而之前方法的坐标是绝对位置(基于当前坐标系的坐标)。
Path path = new Path();
path.moveTo(100,100);
path.lineTo(100,200);
canvas.drawPath(path,mDeafultPaint);
 在这个例子中,先移动点到坐标(100,100)处,之后再连接 点(100,100) 到 (100,200) 之间点直线,非常简单,画出来就是一条竖直的线,那接下来看下一个例子:
在这个例子中,先移动点到坐标(100,100)处,之后再连接 点(100,100) 到 (100,200) 之间点直线,非常简单,画出来就是一条竖直的线,那接下来看下一个例子:
Path path = new Path();
path.moveTo(100,100);
path.rLineTo(100,200);
canvas.drawPath(path,mDeafultPaint);

这个例子中,将 lineTo 换成了 rLineTo 可以看到在屏幕上原本是竖直的线变成了倾斜的线。这是因为最终我们连接的是 (100,100) 和 (200, 300) 之间的线段。
在使用rLineTo之前,当前点的位置在 (100,100) , 使用了 rLineTo(100,200) 之后,下一个点的位置是在当前点的基础上加上偏移量得到的,即 (100+100, 100+200) 这个位置。
此处仅以 rLineTo 为例,只要理解 “绝对坐标” 和 “相对坐标” 的区别,其他方法类比即可。
填充模式
Paint有三种样式,“描边” “填充” 以及 “描边加填充”,我们这里所了解到就是在Paint设置为后两种样式时不同的填充模式对图形渲染效果的影响。
我们要给一个图形内部填充颜色,首先需要分清哪一部分是外部,哪一部分是内部,机器判断图形内外,一般有以下两种方法:(此处所有的图形均为封闭图形,不包括图形不封闭这种情况。)
| 方法 | 判定条件 | 解释 |
|---|---|---|
| 奇偶规则 | 奇数表示在图形内,偶数表示在图形外 | 从任意位置p作一条射线, 若与该射线相交的图形边的数目为奇数,则p是图形内部点,否则是外部点。 |
| 非零环绕数规则 | 若环绕数为0表示在图形外,非零表示在图形内 | 首先使图形的边变为矢量。将环绕数初始化为零。再从任意位置p作一条射线。当从p点沿射线方向移动时,对在每个方向上穿过射线的边计数,每当图形的边从右到左穿过射线时,环绕数加1,从左到右时,环绕数减1。处理完图形的所有相关边之后,若环绕数为非零,则p为内部点,否则,p是外部点。 |
奇偶规则(Even-Odd Rule)
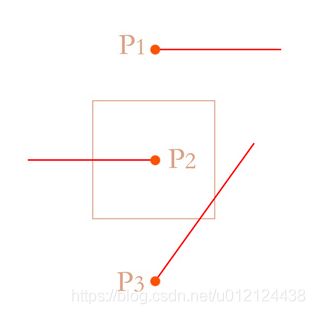 在上图中有一个四边形,我们选取了三个点来判断这些点是否在图形内部。
在上图中有一个四边形,我们选取了三个点来判断这些点是否在图形内部。
P1: 从P1发出一条射线,发现图形与该射线相交边数为0,偶数,故P1点在图形外部。
P2: 从P2发出一条射线,发现图形与该射线相交边数为1,奇数,故P2点在图形内部。
P3: 从P3发出一条射线,发现图形与该射线相交边数为2,偶数,故P3点在图形外部。
非零环绕数规则(Non-Zero Winding Number Rule)
Path中添加图形时需要指定图形的添加方式,是用顺时针还是逆时针,另外我们不论是使用lineTo,quadTo,cubicTo还是其他连接线的方法,都是从一个点连接到另一个点,换言之,Path中任何线段都是有方向性的,这也是使用非零环绕数规则的基础。
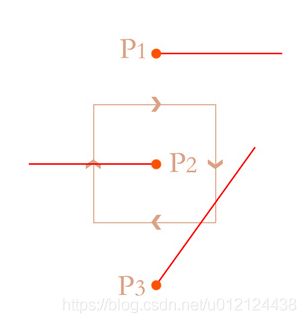 P1: 从P1点发出一条射线,沿射线方向移动,并没有与边相交点部分,环绕数为0,故P1在图形外边。
P1: 从P1点发出一条射线,沿射线方向移动,并没有与边相交点部分,环绕数为0,故P1在图形外边。
P2: 从P2点发出一条射线,沿射线方向移动,与图形点左侧边相交,该边从左到右穿过穿过射线,环绕数-1,最终环绕数为-1,故P2在图形内部。
P3: 从P3点发出一条射线,沿射线方向移动,在第一个交点处,底边从右到左穿过射线,环绕数+1,在第二个交点处,右侧边从左到右穿过射线,环绕数-1,最终环绕数为0,故P3在图形外部。
通常,这两种方法的判断结果是相同的,但也存在两种方法判断结果不同的情况,如下面这种情况:
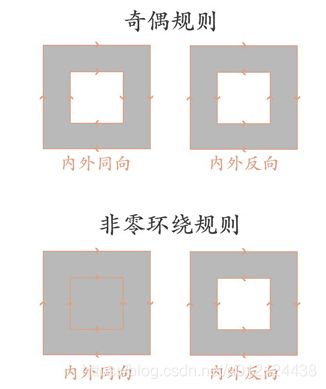 自相交图形
自相交图形
自相交图形定义:多边形在平面内除顶点外还有其他公共点。下图就是一个简单的自相交图形:
 Android中的填充模式
Android中的填充模式
Android中的填充模式有四种,是封装在Path中的一个枚举。
| 模式 | 简介 |
|---|---|
| EVEN_ODD | 奇偶规则 |
| INVERSE_EVEN_ODD | 反奇偶规则 |
| WINDING | 非零环绕数规则 |
| INVERSE_WINDING | 反非零环绕数规则 |
我们可以看到上面有四种模式,分成两对,例如 “奇偶规则” 与 “反奇偶规则” 是一对,它们之间有什么关系呢?
Inverse 和含义是“相反,对立”,说明反奇偶规则刚好与奇偶规则相反,例如对于一个矩形而言,使用奇偶规则会填充矩形内部,而使用反奇偶规则会填充矩形外部,这个会在后面示例中代码展示两者对区别。
Android与填充模式相关的方法
这些都是Path中的方法。
| 方法 | 作用 |
|---|---|
| setFillType | 设置填充规则 |
| getFillType | 获取当前填充规则 |
| isInverseFillType | 判断是否是反向(INVERSE)规则 |
| toggleInverseFillType | 切换填充规则(即原有规则与反向规则之间相互切换) |
奇偶规则与反奇偶规则
mDeafultPaint.setStyle(Paint.Style.FILL); // 设置画布模式为填充
canvas.translate(mViewWidth / 2, mViewHeight / 2); // 移动画布(坐标系)
Path path = new Path(); // 创建Path
//path.setFillType(Path.FillType.EVEN_ODD); // 设置Path填充模式为 奇偶规则
path.setFillType(Path.FillType.INVERSE_EVEN_ODD); // 反奇偶规则
path.addRect(-200,-200,200,200, Path.Direction.CW); // 给Path中添加一个矩形
下面两张图片分别是在奇偶规则于反奇偶规则的情况下绘制的结果,可以看出其填充的区域刚好相反:(白色为背景色,黑色为填充色)


图形边的方向对非零奇偶环绕数规则填充结果的影响
我们之前讨论过给Path添加图形时顺时针与逆时针的作用,除了上次讲述的方便记录外,就是本文所涉及的另外一个重要作用了: “作为非零环绕数规则的判断依据。”
mDeafultPaint.setStyle(Paint.Style.FILL); // 设置画笔模式为填充
canvas.translate(mViewWidth / 2, mViewHeight / 2); // 移动画布(坐系)
Path path = new Path(); // 创建Path
// 添加小正方形 (通过这两行代码来控制小正方形边的方向,从而演示不同的效果)
// path.addRect(-200, -200, 200, 200, Path.Direction.CW);
path.addRect(-200, -200, 200, 200, Path.Direction.CCW);
// 添加大正方形
path.addRect(-400, -400, 400, 400, Path.Direction.CCW);
path.setFillType(Path.FillType.WINDING); // 设置Path填充模式为非零环绕规则
canvas.drawPath(path, mDeafultPaint); // 绘制Path
布尔操作(API19)
布尔操作与我们中学所学的集合操作非常像,只要知道集合操作中等交集,并集,差集等操作,那么理解布尔操作也是很容易的。
布尔操作是两个Path之间的运算,主要作用是用一些简单的图形通过一些规则合成一些相对比较复杂,或难以直接得到的图形。
如太极中的阴阳鱼,如果用贝塞尔曲线制作的话,可能需要六段贝塞尔曲线才行,而在这里我们可以用四个Path通过布尔运算得到,而且会相对来说更容易理解一点。

canvas.translate(mViewWidth / 2, mViewHeight / 2);
Path path1 = new Path();
Path path2 = new Path();
Path path3 = new Path();
Path path4 = new Path();
path1.addCircle(0, 0, 200, Path.Direction.CW);
path2.addRect(0, -200, 200, 200, Path.Direction.CW);
path3.addCircle(0, -100, 100, Path.Direction.CW);
path4.addCircle(0, 100, 100, Path.Direction.CCW);
path1.op(path2, Path.Op.DIFFERENCE);
path1.op(path3, Path.Op.UNION);
path1.op(path4, Path.Op.DIFFERENCE);
canvas.drawPath(path1, mDeafultPaint);
Path的布尔运算有五种逻辑,如下:
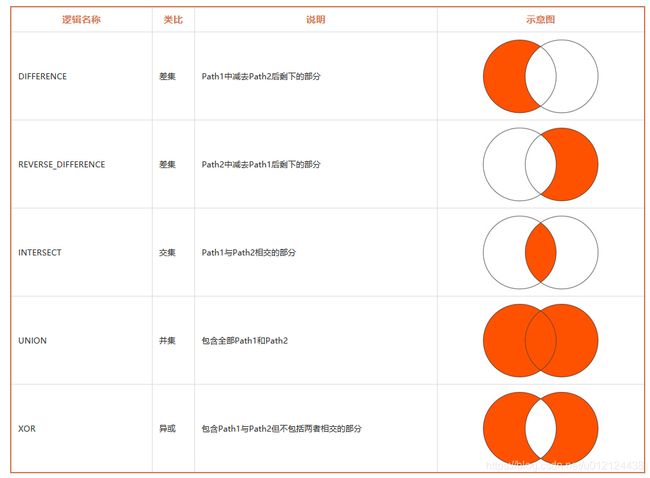 布尔运算方法
布尔运算方法
在Path中的布尔运算有两个方法
boolean op (Path path, Path.Op op)
boolean op (Path path1, Path path2, Path.Op op)
两个方法中的返回值用于判断布尔运算是否成功,它们使用方法如下:
// 对 path1 和 path2 执行布尔运算,运算方式由第二个参数指定,运算结果存入到path1中。
path1.op(path2, Path.Op.DIFFERENCE);
// 对 path1 和 path2 执行布尔运算,运算方式由第三个参数指定,运算结果存入到path3中。
path3.op(path1, path2, Path.Op.DIFFERENCE)
int x = 80;
int r = 100;
canvas.translate(250,0);
Path path1 = new Path();
Path path2 = new Path();
Path pathOpResult = new Path();
path1.addCircle(-x, 0, r, Path.Direction.CW);
path2.addCircle(x, 0, r, Path.Direction.CW);
pathOpResult.op(path1,path2, Path.Op.DIFFERENCE);
canvas.translate(0, 200);
canvas.drawText("DIFFERENCE", 240,0,mDeafultPaint);
canvas.drawPath(pathOpResult,mDeafultPaint);
pathOpResult.op(path1,path2, Path.Op.REVERSE_DIFFERENCE);
canvas.translate(0, 300);
canvas.drawText("REVERSE_DIFFERENCE", 240,0,mDeafultPaint);
canvas.drawPath(pathOpResult,mDeafultPaint);
pathOpResult.op(path1,path2, Path.Op.INTERSECT);
canvas.translate(0, 300);
canvas.drawText("INTERSECT", 240,0,mDeafultPaint);
canvas.drawPath(pathOpResult,mDeafultPaint);
pathOpResult.op(path1,path2, Path.Op.UNION);
canvas.translate(0, 300);
canvas.drawText("UNION", 240,0,mDeafultPaint);
canvas.drawPath(pathOpResult,mDeafultPaint);
pathOpResult.op(path1,path2, Path.Op.XOR);
canvas.translate(0, 300);
canvas.drawText("XOR", 240,0,mDeafultPaint);
canvas.drawPath(pathOpResult,mDeafultPaint);
计算边界
这个方法主要作用是计算Path所占用的空间以及所在位置,方法如下:
void computeBounds (RectF bounds, boolean exact)
它有两个参数:
| 参数 | 作用 |
|---|---|
| bounds | 测量结果会放入这个矩形 |
| exact | 是否精确测量,目前这一个参数作用已经废弃,一般写true即可。 |
// 移动canvas,mViewWidth与mViewHeight在 onSizeChanged 方法中获得
canvas.translate(mViewWidth/2,mViewHeight/2);
RectF rect1 = new RectF(); // 存放测量结果的矩形
Path path = new Path(); // 创建Path并添加一些内容
path.lineTo(100,-50);
path.lineTo(100,50);
path.close();
path.addCircle(-100,0,100, Path.Direction.CW);
path.computeBounds(rect1,true); // 测量Path
canvas.drawPath(path,mDeafultPaint); // 绘制Path
mDeafultPaint.setStyle(Paint.Style.STROKE);
mDeafultPaint.setColor(Color.RED);
canvas.drawRect(rect1,mDeafultPaint); // 绘制边界
重置路径
重置Path有两个方法,分别是reset和rewind,两者区别主要有一下两点:
| 方法 | 是否保留FillType设置 | 是否保留原有数据结构 |
|---|---|---|
| reset | 是 | 否 |
| rewind | 否 | 是 |
这个两个方法应该何时选择呢?
选择权重: FillType > 数据结构
因为“FillType”影响的是显示效果,而“数据结构”影响的是重建速度。


