莫比乌斯反演入门 HDOJ 1695:GCD 、BZOJ 2301: [HAOI2011]Problem b

这篇博客对莫比乌斯反演入门很有帮助 http://blog.csdn.net/nexplain/article/details/18954219

下面我所说的都基于上面这篇博客的内容。

莫比乌斯反演有两种形式（mu表示莫比乌斯函数）：

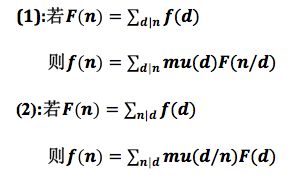
HDOJ1695 GCD

求1<=x<=n,1<=y<=m中gcd(x,y)==k的(x,y)组数，注意(a,b)和(b,a)视为同一情况。

相当于计算1<=x<=n/k，1<=y<=m/k的数中有多少对互质(即gcd(x,y)==1)。

进一步转化出所求即为

f(1)=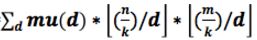

令n/=k，m/=k

算出1<=x<=n，1<=y<=m中的互质情况数，减去1<=x<=min(n,m)、1<=y<=min(n,m)中互质情况的一半就是答案

为什么是min(n,m)呢？因为(a,b)、(b,a)这种重复情况，a、b肯定属于同一范围，而且这一范围是较小的那一个范围。

假设n

所以有重复情况的(x,y)，一定在公共（交叉）区间内。

因此上界取min(n,m)，省去了一定计算量。

代码体现在：

ans1+=(LL)mu[i]*(b/i)*(b/i);

完整代码

#include 
#include 
#include 
#include 
#include 
#define mst(a,b) memset(a,b,sizeof(a))
typedef long long LL;
using namespace std;
const int N = 100005;
bool check[N+10];
int prime[N+10],mu[N+10];

//莫比乌斯函数模板
void Mobius()
{
    memset(check,false,sizeof(check));
    mu[1] = 1;
    int tot = 0;
    for(int i=2;i<=N;i++){
        if(!check[i]){
            prime[tot ++] = i;
            mu[i] = -1;
        }
        for(int j=0;j N) break;
            check[i * prime[j]] = true;
            if(i % prime[j] == 0){
                mu[i * prime[j]] = 0;
                break;
            }
            else
                mu[i * prime[j]] = -mu[i];
        }
    }
}

int main()
{
    int a,b,c,d,k,T,cas=1;
    Mobius();
    cin>>T;
    while(T--){
        scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
        if(k==0){
            printf("Case %d: 0\n",cas++);
            continue;
        }
        b/=k;
        d/=k;
        if(b>d) swap(b,d);
        LL ans=0,ans1=0;
        for(int i=1;i<=b;i++){
            ans+=(LL)mu[i]*(b/i)*(d/i);
            ans1+=(LL)mu[i]*(b/i)*(b/i);
        }
        ans-=ans1/2;
        printf("Case %d: %lld\n",cas++,ans);
    }

    return 0;
}

BZOJ 2301: [HAOI2011]Problem b

每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

#include 
#include 
#include 
#include 
#include 
#define mst(a,b) memset(a,b,sizeof(a))
typedef long long LL;
using namespace std;
const int N = 100000;
bool check[N+5];
int prime[N+5],mu[N+5],sum[N+5];

//莫比乌斯函数模板
void Mobius()
{
    memset(check,false,sizeof(check));
    mu[1] = 1;
    int tot = 0;
    for(int i=2;i<=N;i++){
        if(!check[i]){
            prime[tot ++] = i;
            mu[i] = -1;
        }
        for(int j=0;j N) break;
            check[i * prime[j]] = true;
            if(i % prime[j] == 0){
                mu[i * prime[j]] = 0;
                break;
            }
            else
                mu[i * prime[j]] = -mu[i];
        }
    }
}

LL cal(int n,int m,int k){
    LL ans=0;
    n/=k;
    m/=k;
    if(n>m) swap(n,m);
    for(int i=1,last;i<=n;i=last+1){            //i是不变块的左边界,last是不变块的右边界
        last = min(n/(n/i),m/(m/i));            //根据左边界算出右边界
        ans+=(LL)(sum[last]-sum[i-1])*(n/i)*(m/i);
    }
    return ans;
}

int main()
{
    int a,b,c,d,k,T;
    Mobius();
    sum[0]=0;
    for(int i=1;i<=N;i++)
        sum[i]=sum[i-1]+mu[i];

    cin>>T;
    while(T--){
        scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
        if(k==0){
            printf("0\n");
            continue;
        }

        LL ans1=cal(b,d,k);
        LL ans2=cal(a-1,d,k);
        LL ans3=cal(b,c-1,k);
        LL ans4=cal(a-1,c-1,k);
        LL ans=ans1-ans2-ans3+ans4;         //容斥原理

        printf("%lld\n",ans);
    }

    return 0;
}