yalmip简单的例子
YALMIP应用篇
个人blog
yalmip是一个在matlab内的建模工具包,能够用一套统一的建模语言来构建约束,调用其他的求解器,减少了单独学习其他语言的浪费,我根据论文
俞武扬. YALMIP工具箱在运筹学实验教学中的应用[J]. 实验室研究与探索, 2017(8).
由于该论文的代码有错误,我改写了一下 以下例子为论文中的例子 1.一般线性规划 2.运输问题 3.背包问题 4.指派问题 5.最短路问题
yalmip基本格式
- 创建决策变量
- 目标函数
z - 约束条件设置
C - 参数设置
ops = sdpsetting('solver','Cplex','verbose',0); verbose:显示冗余度0为只显示结果 - 求解
result = solvesdp(C,z,ops)
一般线性规划
model
min Z = C X s.t. { A X = b X ⩾ 0 \begin{array}{l}{\min Z=C X} \\ {\text { s.t. }\left\{\begin{array}{l}{A X=b} \\ {X \geqslant 0}\end{array}\right.}\end{array} minZ=CX s.t. {AX=bX⩾0
例子
min Z = 12 x 1 + 5 x 2 + 8 x 3 s.t. { 2 x 1 + 3 x 2 + x 3 ⩾ 30 4 x 1 + x 2 + 5 x 3 ⩾ 15 x 1 , x 2 , x 3 ⩾ 0 \min Z=12 x_{1}+5 x_{2}+8 x_{3}\\ \text { s.t. }\left\{\begin{array}{l}{2 x_{1}+3 x_{2}+x_{3} \geqslant 30} \\ {4 x_{1}+x_{2}+5 x_{3} \geqslant 15} \\ {x_{1}, x_{2}, x_{3} \geqslant 0}\end{array}\right. minZ=12x1+5x2+8x3 s.t. ⎩⎨⎧2x1+3x2+x3⩾304x1+x2+5x3⩾15x1,x2,x3⩾0
clear;clc;close all;
c = [12 5 8];
A = [2 3 1; 4 1 5];
b = [30; 15];
%决策变量
x = sdpvar(3,1);
%目标函数
z = c*x;
%添加约束
%C = [];
%C = [C; A*x >= b];
%C = [C;x>=0];
C=[A*x >= b,x>=0];
ops=sdpsettings('verbose',0);
%求解
result = optimize(C,z,ops);
if result.problem == 0 %求解成功
x_star=double(x)
z_star=double(z)
else
disp('求解过程中出错');
end
警告: 文件: C:\Program Files\IBM\ILOG\CPLEX_Studio_Community128\cplex\matlab\x64_win64\@Cplex\Cplex.p 行: 965 列: 0
在嵌套函数中定义 "changedParam" 会将其与父函数共享。在以后的版本中,要在父函数和嵌套函数之间共享 "changedParam",请在父函数中显式定义它。
> In cplexoptimset
In sdpsettings>setup_cplex_options (line 617)
In sdpsettings (line 145)
x_star =
0
9.6429
1.0714
z_star =
56.7857
运输问题
model
min Z = ∑ i = 1 m ∑ j = 1 n c i j x i j s.t. { ∑ j = 1 n x i j ⩽ a i , i = 1 , 2 , ⋯ , m ∑ i = 1 m x i j ⩾ b j , j = 1 , 2 , ⋯ , n x i j ⩾ 0 , i = 1 , 2 , ⋯ , m ; j = 1 , 2 , ⋯ , n \min Z=\sum_{i=1}^{m} \sum_{j=1}^{n} c_{i j} x_{i j}\\ \text { s.t. }\left\{\begin{array}{ll}{\sum\limits_{j=1}^{n} x_{i j} \leqslant a_{i},} & {i=1,2, \cdots, m} \\ {\sum\limits_{i=1}^{m} x_{i j} \geqslant b_{j},} & {j=1,2, \cdots, n} \\ {x_{i j} \geqslant 0,} & {i=1,2, \cdots, m ; j=1,2, \cdots, n}\end{array}\right. minZ=i=1∑mj=1∑ncijxij s.t. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧j=1∑nxij⩽ai,i=1∑mxij⩾bj,xij⩾0,i=1,2,⋯,mj=1,2,⋯,ni=1,2,⋯,m;j=1,2,⋯,n
例子
clear;clc;close all;
c = [1 3 5 7 13; 6 4 3 14 8; 13 3 1 7 4;
1 10 12 7 11];
a = [40 50 30 80];
b = [10 20 15 18 25];
%决策变量
x = intvar(4,5);
%目标函数
z = sum(sum(c.*x));
%添加约束
C = [];
for i=1:4
C = [C; sum(x(i,:))<=a(i)];
end
for j=1:5
C = [C;sum(x(:,j))>=b(j)];
end
C = [C;x>=0];
ops=sdpsettings('verbose',0);
result = optimize(C,z,ops);
if result.problem == 0 %求解成功
x_star = double(x)
z_star = double(z)
else
disp('求解过程中出错');
end
x_star =
2 20 0 18 0
0 0 10 0 0
0 0 5 0 25
8 0 0 0 0
z_star =
331
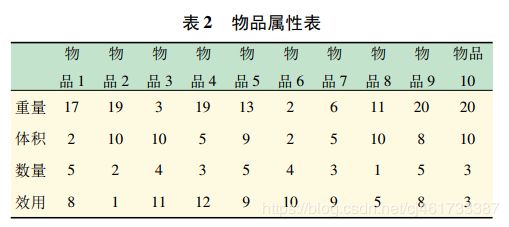
背包问题
model
max Z = ∑ i = 1 n c i x i s.t. { ∑ i = 1 n x i w i ⩽ W ∑ i = 1 n x i v i ⩽ V 0 ⩽ x i ⩽ n i 且为整数 \max Z=\sum_{i=1}^{n} c_{i}x_{i} \\ \text { s.t. }\left\{\begin{array}{l}{\sum_{i=1}^{n} x_{i} w_{i} \leqslant W} \\ {\sum_{i=1}^{n} x_{i} v_{i} \leqslant V} \\ {0 \leqslant x_{i} \leqslant n_{i}\quad \text{且为整数}}\end{array}\right. maxZ=i=1∑ncixi s.t. ⎩⎨⎧∑i=1nxiwi⩽W∑i=1nxivi⩽V0⩽xi⩽ni且为整数
例子
clear;clc;close all;
c = [8 1 11 12 9 10 9 5 8 3]; %效用
w = [17 19 3 19 13 2 6 11 20 20]; %重量
v = [2 10 10 5 9 2 5 10 8 10]; %体积
n = [5 2 4 3 5 4 3 1 5 3]; %数量
%决策变量
x = intvar(10,1);
%目标函数
z = -(c*x);
%添加约束
C = [];
C = [C,w*x<=80];
C = [C,v*x<=60];
C = [C,0<=x<=n];
ops=sdpsettings('verbose',0);
%求解
result = optimize(C,z,ops);
if result.problem == 0 %求解成功
x_star = double(x)
z_star = double(-z)
else
disp('求解过程中出错');
end
x_star =
1
0
3
1
0
4
3
0
0
0
z_star =
120
最短路问题
% 利用yamlip求解最短路问题
clear;clc;close all;
D = load('1.txt');
n = size(D,1);
% 决策变量
x = binvar(n,n,'full');
% 目标
z=sum(sum(D.*x));
% 约束添加
C=[];
C = [C,(sum(x(1,:))-sum(x(:,1))==1)];
C = [C,(sum(x(n,:))-sum(x(:,n))==-1)];
for i=2:(n-1)
C = [C,(sum(x(i,:))-sum(x(:,i))==0)];
end
ops=sdpsettings('verbose',0);
% 求解
result=solvesdp(C,z,ops);
if result.problem == 0
x_star = value(x)
z_star = value(z)
else
disp('求解过程中出错');
end
x_star =
NaN 1 0 0 0 0 0
0 NaN 0 0 1 0 0
0 0 NaN 0 0 0 0
0 0 0 NaN 0 0 0
0 0 0 0 NaN 0 1
0 0 0 0 0 NaN 0
0 0 0 0 0 0 NaN
z_star =
5
指派问题
model
min Z = ∑ i = 1 n ∑ j = 1 n c i j x i j s.t. { ∑ i = 1 n x i j = 1 , j = 1 , 2 , ⋯ , n ∑ j = 1 n x i j = 1 , i = 1 , 2 , ⋯ , n x i j ∈ { 0 , 1 } , i , j = 1 , 2 , ⋯ , n \min Z=\sum_{i=1}^{n} \sum_{j=1}^{n} c_{i j} x_{i j}\\ \text { s.t. }\left\{\begin{array}{ll}{\sum_{i=1}^{n} x_{i j}=1,} & {j=1,2, \cdots, n} \\ {\sum_{j=1}^{n} x_{i j}=1,} & {i=1,2, \cdots, n} \\ {x_{i j} \in\{0,1\},} & {i, j=1,2, \cdots, n}\end{array}\right. minZ=i=1∑nj=1∑ncijxij s.t. ⎩⎨⎧∑i=1nxij=1,∑j=1nxij=1,xij∈{0,1},j=1,2,⋯,ni=1,2,⋯,ni,j=1,2,⋯,n
例子
clear;clc;close all;
c =load('zhipai.txt')
%决策变量
x = binvar(5,5,'full');
%目标函数
z = sum(sum(c.*x));
%添加约束
C = [];
C = [C;sum(x,1)==1]; % 1 横向相加
C = [C;sum(x,2)==1]; % 2 纵向相加
ops=sdpsettings('verbose',0);
%求解
result = optimize(C,z,ops);
if result.problem == 0 %求解成功
x_star = double(x)
z_star = double(z)
else
disp('求解过程中出错');
end
c =
12 7 9 7 9
8 9 6 6 6
7 17 12 14 9
15 14 6 6 10
4 10 7 10 9
x_star =
0 1 0 0 0
0 0 0 1 0
0 0 0 0 1
0 0 1 0 0
1 0 0 0 0
z_star =
32