整 数 规 划——分支定界、割平面、指派问题(自学)
整 数 规 划
问题的提出
整数规划中如果所有的变数都限制为 (非负 ) 整数, 就称为纯整数规划 ( pure integer programming )或称为全整数规划( all integer programming) ; 如果仅一部分变数限制为整数,则称为混合整数计划( mixed integer programming)。整数规划的一种特殊情形是 0 -1 规划,它的变数取值仅限于 0 或 1。
1 分支定界解法
可用于解纯整数或混合的整数规划问题。在 20 世纪 60 年代初由 Land Doig 和 Dakin 等人提出。
设有最大化的整数规划问题 A, 与它相应的线性规划为问题 B, 从解问题 B 开始,若其最优解不符合 A 的整数条件,那么 B 的最优目标函数必是 A 的最优目标函数 z的上界, 记作 z;而 A 的任意可行解的目标函数值将是 z的一个下界 z。分支定界法就是将 B 的可行域分成子区域(称为分支)的方法, 逐步减小和增大 z, 最终求到 z*。现用下例来说明:
[例子来自运筹学课本116页]
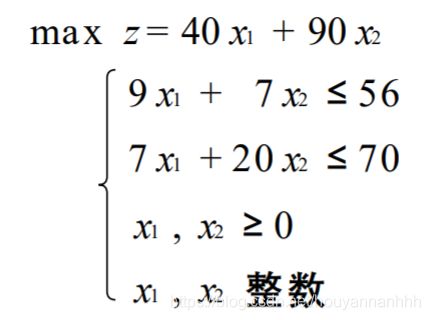
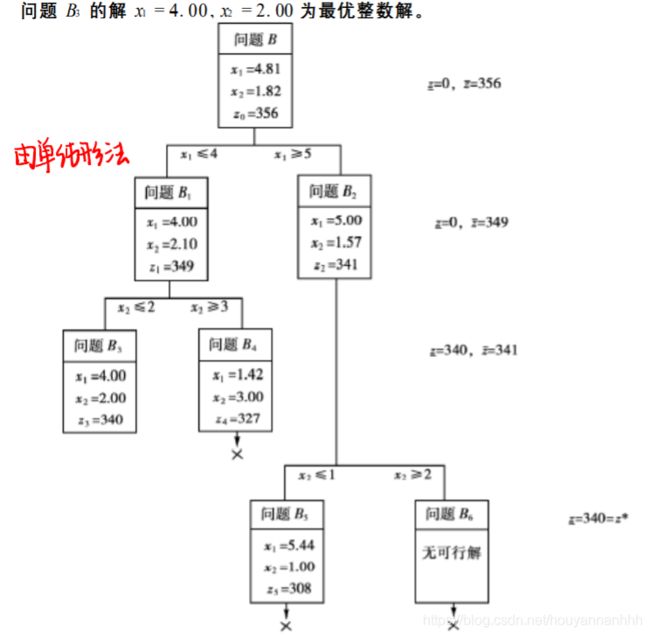
先不考虑整数条件,解相应的线性规划B
x 1 = 4.81 , x 2 = 1.82 , x 3 = 356 x_1=4.81,x_2=1.82,x_3=356 x1=4.81,x2=1.82,x3=356


2 割平面解法
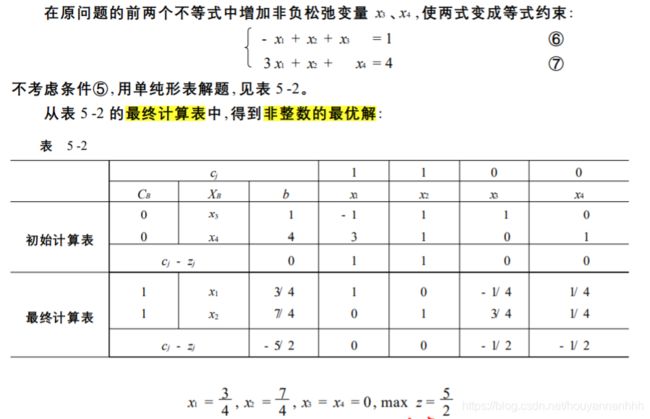
首先不考虑变量 xi是整数这一条件,但增加线性约束条件( 用几何术语,称为割平面) 使得由原可行域中切割掉一部分,这部分只包含非整数解, 但没有切割掉任何整数可行解。这个方法就是指出怎样找到适当的割平面(不见得一次就找到) ,使切割后最终得到这样的可行域, 它的一个有整数坐标的极点恰好是问题的最优解。这个方法是 R .E .Gomory 提出来的, 所以又称为Gomory 的割平面法。以下只讨论纯整数规划的情形, 现举例说明。
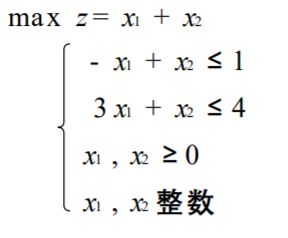
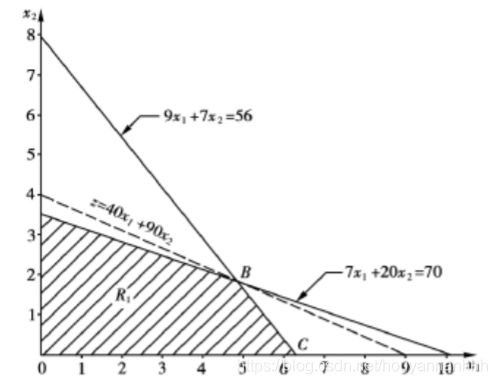
求得相应的线性规划的最优解:
x 1 = 3 / 4 , x 2 = 7 / 4 , m a x z = 10 / 4 x1 =3/4, x2 =7/4, max z =10/4 x1=3/4,x2=7/4,maxz=10/4

它就是图 中域 R 的极点 A, 但不合于整数条件。现设想,如能找到像 CD 那样的直线去切割域 R, 去掉三角形域 ACD,那么具有整数坐标的 C点( 1, 1) 就是域 R′的一个极点,如在域 R′上求解, 而得到的最优解又恰巧在 C 点就得到原问题的整数解,所以解法的关键就是怎样构造一个这样的“割平面”CD, 尽管它可能不是唯一的, 也可能不是一步能求到的。




3 指 派 问 题
指派哪个人去完成哪项任务,使完成 n 项任务的总效率最高( 或所需总时间最小) 。这类问题称为指派问题或分派问题( assignment problem )。
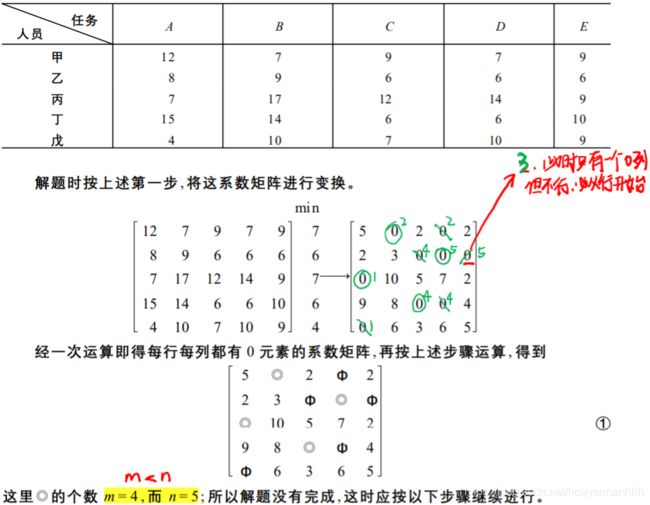
例 7 有一份中文说明书, 需译成英、日、德、俄四种文字。分别记作 E、J、G、R。现有甲、乙、丙、丁四人。他们将中文说明书翻译成不同语种的说明书所需时间如表所示。问应指派何人去完成何工作,使所需总时间最少 ?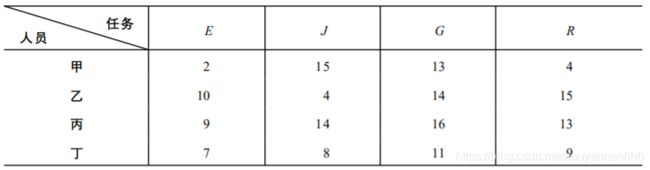
解题时需引入变量 xi j ; 其取值只能是 1 或 0