整数规划----割平面法的Matlab实现
在纯整数规划问题中,有一种求解方法叫做割平面法,它是通过不断地求解最优解,然后每次引入一个松弛变量,将其加入约束条件中,最终求得最优解的这样的一个循环过程。
- 根据b矩阵的值选择利用单纯形法或者对偶单纯形法求解松弛问题
- 判断此时解是否满足整数规划问题,若满足则结束循环,否则继续下一步;
- 从解得的b矩阵中选择和对应整数差值最大的值的行位置作为新加入的割平面约束的对应行
- ∑ \sum ∑选中行中非基矩阵乘上对应的 x i x_i xi<=-(选中的最大差值),即 ∑ j ∈ k ( − f i 0 , j ) x j ≤ − f i 0 \sum_{j\in k}(-f_{i_{0},j})x_j\leq-f_{i_0} ∑j∈k(−fi0,j)xj≤−fi0
- 引入松弛变量,将3化为标准型加入约束条件中,重复上述过程。
过程图解:

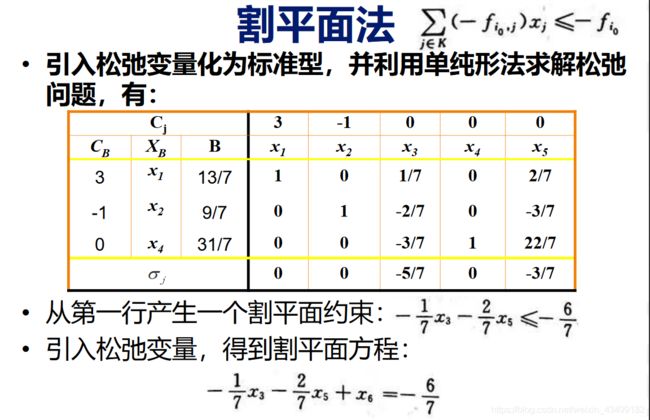
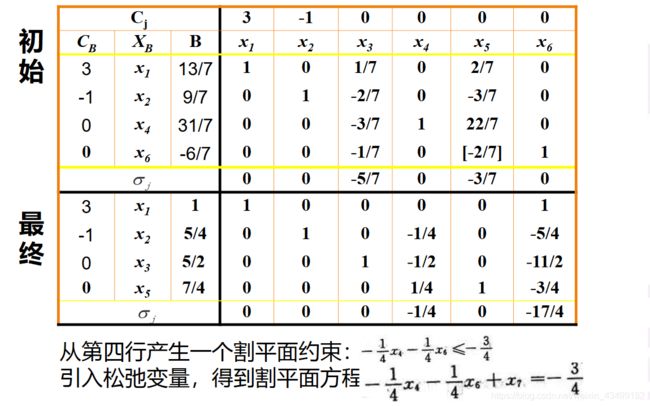
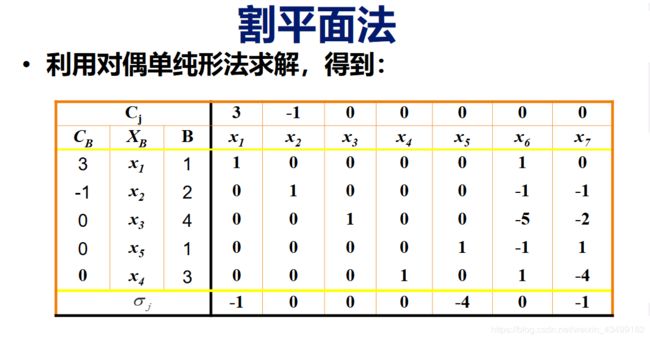 求解样例:
求解样例:
 Matlab实现:
Matlab实现:
只查找一次基矩阵,下一次使用的矩阵是上一次更新过的,不是最原始矩阵。调用的单纯形法和对偶单纯形法是我之前自己写的,改了点参数。
close all;
clear all;
format rat;%结果以分数形式显示
A=[-1,3,1,0;
7,1,0,1];
b=[6,35]';
c=[7,9,0,0];
n=4;
m=2;
% A=[1,1,1,0,0;
% -1,1,0,1,0;
% 6,2,0,0,1];
% b=[5,0,21]';
% c=[2,1,0,0,0];
% n=5;
% m=3;
[xstar,fxstar,iter] = Gomory(A,b,c,n,m)
function [xstar,fxstar,iter] = Gomory(A,b,c,n,m)
%先选出初始单位阵
init_eye_pos=nchoosek(1:1:n,m);
[row,col]=size(init_eye_pos);
for i = 1:row
tmp_init_eye=init_eye_pos(i,:);
init_eye=A(:,tmp_init_eye);
flag=is_ones(init_eye);
if flag==1
fin_ji_x=tmp_init_eye;
break;
end
end
while 1
%解方程,b都大于0就用单纯形法,否则就用对偶单纯形法
if min(b)>=0
disp("调用单纯形法");
%fin_ji_x、fin_A、fin_b 返回最优解时对应的的基矩阵、A矩阵、b矩阵
%传入参数ji_x,在原先基础上作为基矩阵直接计算
[x_opt,fx_opt,iter,fin_ji_x,fin_A,fin_b]=Simplex_eye(A,b,c,n,m,fin_ji_x)
else
disp("调用对偶单纯形法");
[x_opt,fx_opt,iter,fin_ji_x,fin_A,fin_b]=DSimplex_eye(A,b,c,n,m,fin_ji_x)
end
%每次要更改基矩阵,增加直接加1,不更新的话程序每次都要重新寻找基矩阵,系数对应不上
tmp_ji_x=zeros(1,m+1);%基矩阵前m个元素直接复制,第m+1个赋值n+1
for ji_pos=1:m
tmp_ji_x(1,ji_pos)=fin_ji_x(1,ji_pos);
end
tmp_ji_x(1,m+1)=n+1;
fin_ji_x=tmp_ji_x;
%判断是否已经解出了整数最优解
flag_zhengshu=1;%flag_zhengshu初始化为1,只要有一个不是整数,flag_zhengshu赋值0
for pos_x = 1:m
if abs(round(x_opt(pos_x,1))-x_opt(pos_x,1))>=1e-3%判断整数条件
flag_zhengshu=0;
break;
end
end
if flag_zhengshu==1%如果解全是整数,满足条件,循环结束
xstar=x_opt;
fxstar=fx_opt;
break;
end
%选择增加约束条件的行
choose_row_value=0;%记录差值大小,初始化为0
for pos_row = 1:m%循环遍历b矩阵,找出和整数相差最大的那个数
tmp=get_max_chazhi(fin_b(pos_row,1));
if tmp>choose_row_value
choose_row_value=tmp;
choose_row_pos = pos_row;%标记当前最大插值的位置
end
end
n=n+1;
m=m+1;
iter=iter+1;
%更新矩阵所有系数,在原先基础上增加一行一列(全0),第(m,n)=1
tmp_A5=zeros(m,n);
tmp_b5=zeros(m,1);
tmp_c5=zeros(1,n);
for i5=1:m-1
for j5=1:n-1
tmp_A5(i5,j5)=fin_A(i5,j5);
end
tmp_b5(i5,1)=fin_b(i5,1);
end
tmp_A5(m,n)=1;
for i5=1:n-1
tmp_c5(1,i5)=c(i5);
end
%加上约束条件
for add_pos = 1:n-1
flag_not_ji=1;
for ji=1:m-1
if add_pos==fin_ji_x(ji)
flag_not_ji=0;
break;
end
end
if flag_not_ji==1
tmp_A5(m,add_pos)=-get_max_chazhi(fin_A(choose_row_pos ,add_pos));
end
end
tmp_b5(m,1)=-choose_row_value;
A=tmp_A5
b=tmp_b5
c=tmp_c5
n
m
end
end
%函数计算和整数的差值
function [max_chazhi] = get_max_chazhi(x)%返回差值的绝对值
if x>=0
max_chazhi=x-floor(x);
else
max_chazhi=x-floor(x);
end
end
function [x_opt,fx_opt,iter,fin_ji_x,fin_A,fin_b]=Simplex_eye(A,b,c,n,m,ji_x)
iter=0;
%循环迭代求解
chi_da=(zeros(m))';
sigma=zeros(1,n)';
CB=(zeros(1,m))';
for cb_pos=1:m
for c_pos=1:n
if ji_x(cb_pos)==c_pos
CB(cb_pos,1)=c(c_pos);
end
end
end
tmp_A=A;
flag=1;
while flag
iter=iter+1;
%更新sigma,确定换入基
for pos_c = 1:n
sigma(pos_c,1)=c(pos_c);
for pos_tmp = 1:m
sigma(pos_c,1)=sigma(pos_c,1)-CB(pos_tmp,1)*tmp_A(pos_tmp,pos_c);
end
end
max_sigma=-1;
for pos_sigma = 1:n
if sigma(pos_sigma,1)>max_sigma
max_sigma_pos=pos_sigma;
max_sigma=sigma(pos_sigma,1);
end
end
if max_sigma<=0%此时已经找到最优解
x_opt=(zeros(1,n))';
x_opt(ji_x,1)=b(:,1);
fx_opt=0;
for pos_x1 = 1:n
fx_opt=fx_opt+c(pos_x1)*x_opt(pos_x1,1);
end
fin_A=tmp_A;
fin_b=b;
fin_ji_x=ji_x;
flag=0;
else
%更新chi_da,确定换出基
for chi_da_pos=1:m
chi_da(chi_da_pos,1)=b(chi_da_pos,1)/tmp_A(chi_da_pos,max_sigma_pos);
end
min_chi_da=-1;
for chi_da_pos=1:m
if chi_da(chi_da_pos,1)>0 && tmp_A(chi_da_pos,max_sigma_pos)>0%找出min(chi_da)>0的值且对应左边的值要>0(老师说的)
if min_chi_da==-1 || chi_da(chi_da_pos,1)=0%此时已经找到最优解
x_opt=(zeros(1,n))';
x_opt(ji_x,1)=b(:,1);
fx_opt=0;
for pos_x2 = 1:n
fx_opt=fx_opt+c(pos_x2)*x_opt(pos_x2,1);
end
fin_A=tmp_A;
fin_b=b;
fin_ji_x=ji_x;
flag=0;
break;
else
%更新sigma,确定换入基
for pos_c = 1:n
sigma(1,pos_c)=c(1,pos_c);
for pos_tmp = 1:m
sigma(1,pos_c)=sigma(1,pos_c)-CB(pos_tmp,1)*tmp_A(pos_tmp,pos_c);
end
end
b
CB
c
sigma
tmp_A
if max(sigma)>0
flag=0;
disp("存在无界解!");
break;
end
min_sigma=99999999;
%找出sigma/y_(i,k)中最小的正数作为换入基,否则无解
for i=1:n
if i==min_b_pos
continue;
end
flag_ji=1;
for j=1:m
if ji_x(j)==i
flag_ji=0;
break;
end
end
if flag_ji==1&&(tmp_A(min_b_pos_tmp,i)<0)
temp=(sigma(1,i)/tmp_A(min_b_pos_tmp,i)-0);
% if min_sigma<=temp||abs(round(min_sigma-temp)-(min_sigma-temp)) < 1e-3
if min_sigma>temp
min_sigma=temp;
min_sigma_pos=i;
end
end
end
out_x_pos=min_b_pos%换出基
in_x_pos=min_sigma_pos%换入基
for in_out = 1:m
if ji_x(in_out)==out_x_pos
ji_x(in_out)=in_x_pos;
CB(in_out,1)=c(in_x_pos);
break;
end
end
%对矩阵执行初等变换,因为单纯形法只有换入基的列变化,所以只需将换入基的列化为换出基的列的形式即可
%将换入基对应的点值化为1
tmp_beishu=tmp_A(in_out,ji_x(in_out));
for change_1 =1:n
tmp_A(in_out,change_1)=tmp_A(in_out,change_1)/tmp_beishu;
end
b(in_out,1)=b(in_out,1)/tmp_beishu;%记得将b列的值也要更新
%矩阵内部的初等变换
for change_pos =1:m
if change_pos~=in_out%此列不是换入基
beishu=tmp_A(change_pos,in_x_pos);
for tt=1:n%暴力更新这一行的值
tmp_A(change_pos,tt)=tmp_A(change_pos,tt)-beishu*tmp_A(in_out,tt);
end
b(change_pos,1)=b(change_pos,1)-beishu*b(in_out,1);%同步更新b的值
end
end
end
iter=iter+1;
end
end
function [flag]=is_ones(a)%判断矩阵是否为单位阵
flag=1;
[row_a,col_a]=size(a);
tmp_a=zeros(row_a);%对应的列只有一个1,其他全是0,否则flag=flase;
for i1 =1:row_a
for j1 = 1:col_a
if a(i1,j1)==1 && tmp_a(j1)==0
tmp_a(j1)=1;
elseif a(i1,j1)==0
continue;
else
flag=0;
break;
end
end
end
for i1 =1:row_a
if tmp_a(i1)==0
flag=0;
break;
end
end
end