Min_25筛--简明版
强烈推荐链接
一.前置技能
- 埃式筛法:标记素数的倍数
(线性筛是标记每个数的素数倍数)
- 积性函数性质:

(积性函数比如欧拉函数需要条件gcd(a,b)=1,完全积性函数不需要)
二.适用范围
min2.5筛:质数幂的多项式(完全积性函数)
(杜教筛:可以利用狄利克雷卷积转换为数论函数,方便求前缀和)
显然min2.5筛似乎适用更广些
三.算法思路
首先我们定义:
![]()
g(n,0)表示不对合数做限制,因此是所有数的k次幂的和
但我们要只保留所有素数k次幂的和,
最终得到g(n,INF)
每一轮类似埃式筛法的过程筛掉不满足的数,g(n,j)便代表:对 2~n做埃拉托斯特尼筛法 ,j 轮后剩下的所有数的 k 次幂和,
注意!g(n,j)包括 prime1,..primej 这些处理过的质数。
每轮从j-1→j,筛掉了f(i)
类似埃式筛法,我们只需筛n>=primej^2的部分,过程如下:
①n<=primej^2的部分已经在前面几轮被筛掉,![]()
②n>=primej^2,则要筛掉大于的部分,这部分可以用积性函数性质:
![]()
f(i/primej)可以用g表示,因为n/primej>=n,所以g已经包含了前j-1轮已经筛出来的质数部分,减多了这部分要加回来
③先算出![]() 内质数幂的和的式子:
内质数幂的和的式子:
④最终计算:
我们定义:(注意没有or了,即使是质数,也受到本身>primeb约束)
记忆化:
不记忆化:
若是质数,利用筛出了![]() 的质数和(注意最小质数要求大于b,所以要减去小于b的部分)(g-g那部分)
的质数和(注意最小质数要求大于b,所以要减去小于b的部分)(g-g那部分)
若是合数,枚举最小质因子的次数,累加即可(前半部分是除掉最小质数其他合数的贡献,后半部分是该质数的t次方的贡献)
四.代码
推荐参考链接
递归版
递推版
(暂)参考洛谷模板,注意预处理n/i的值以及加上f(1)的值
#include
#define il inline
#define vd void
#define mod 1000000007
typedef long long ll;
il ll gi(){
ll x=0,f=1;
char ch=getchar();
while(!isdigit(ch))f^=ch=='-',ch=getchar();
while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
return f?x:-x;
}
ll n;
int qt;
int pr[100010],yes[100010],cnt,gp1[100010],gp2[100010];
ll w[200010],sw;
int g1[200010],g2[200010];
int id1[100010],id2[100010];//预处理n/i的值,分别小于大于根号n
il int S(ll x,int y){
if(pr[y]>=x)return 0;
int p=x<=qt?id1[x]:id2[n/x];
int ret=((0ll+g2[p]-g1[p]-(gp2[y]-gp1[y]))%mod+mod)%mod;//p^k^2-p^k
for(int i=y+1;i<=cnt&&1ll*pr[i]*pr[i]<=x;++i){
ll pe=pr[i];
for(int e=1;pe<=x;++e,pe*=pr[i]){
int o=pe%mod;
ret=(ret+1ll*o*(o-1)%mod*(S(x/pe,i)+(e!=1)))%mod;
}
}
return ret;
}
int main(){
n=gi();qt=sqrt(n);
yes[1]=1;
for(int i=2;i<=qt;++i){
if(!yes[i])pr[++cnt]=i;
for(int j=1;j<=cnt&&i*pr[j]<=qt;++j){
yes[i*pr[j]]=1;
if(i%pr[j]==0)break;
}
}
for(int i=1;i<=cnt;++i)gp1[i]=(gp1[i-1]+pr[i])%mod,gp2[i]=(gp2[i-1]+1ll*pr[i]*pr[i])%mod;//递推时用的质数处F前缀和
for(ll l=1,r;l<=n;l=r+1){//预处理(n/i) & 计算g的j=0边界,边界就是F'的前缀和,由于质数处F(p)是多项式所以可以快速算
r=n/(n/l);w[++sw]=n/r;
g1[sw]=w[sw]%mod;
g2[sw]=(1ll*g1[sw]*(g1[sw]+1)%mod*(g1[sw]*2+1)%mod*166666668%mod-1)%mod;//1..w[sw]平方和
g1[sw]=(1ll*g1[sw]*(g1[sw]+1)%mod*500000004-1)%mod;//1..w[sw]等差数列和
if(n/r<=qt)id1[n/r]=sw;else id2[r]=sw;
}
//j从1到|P|递推g
for(int i=1;i<=cnt;++i){
ll sqr_pi=1ll*pr[i]*pr[i];
for(int j=1;j<=sw&&sqr_pi<=w[j];++j){
ll p=w[j]/pr[i];
p=(p<=qt?id1[p]:id2[n/p]);//定位p的坐标
g1[j]=(g1[j]-1ll*pr[i]*(g1[p]-gp1[i-1]+mod)%mod+mod)%mod;
g2[j]=(g2[j]-1ll*pr[i]*pr[i]%mod*(g2[p]-gp2[i-1]+mod)%mod+mod)%mod;
}
}
printf("%d\n",(S(n,0)+1)%mod);
return 0;//}
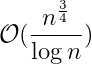
![g(n,j)=\sum_{i=2}^nf(i) [i\subseteq prime \quad or \quad {min_np>prime_j}] (min_np\quad is \quad the \quad smallest \quad prime \quad in\quad n)](http://img.e-com-net.com/image/info8/a82b5ee79fbb4359a589077f098425c3.gif)
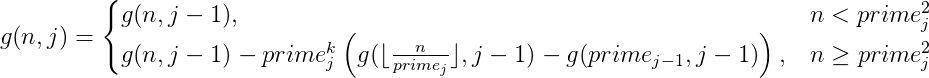
![S(a,b)=\sum_{i=2}^a [pmin_i\ge prime_b]f(i)](http://img.e-com-net.com/image/info8/2bfb423f0856434e89d13eb062be34ad.gif)