深度学习——感知机
一、感知机
感知机接受多个输入信号，输出一个信号。⼀个感知器接受⼏个⼆进制输⼊， x 1 , x 2 , . . . ， x_1, x_2, . . .， x1,x2,...，并产⽣⼀个⼆进制输出：
示例中的感知机有三个输入， x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3。通常可以有更多的或者更少的输入。
为了产生一个简单的规则来计算输出。为此引⼊了“权重”， w 1 , w 2 , . . . ， w_1 , w_2 , . . .， w1,w2,...，表⽰相应输⼊对于输出重要性的实数。神经元的输出，0或者1，则由分配权重后的总和 ∑ j w j x j \displaystyle \sum _jw_j x_j j∑wjxj⼩于或者⼤于⼀些阈值决定。和权重⼀样， 阈值是⼀个实数，⼀个神经元的参数。⽤更精确的代数形式：
y = { 0 w 1 x 1 + w 2 x 2 ≤ θ 1 w 1 x 1 + w 2 x 2 > θ y=\left\{ \begin{matrix}0\qquad w_1x_1+w_2x_2\leq\theta \\ \\ 1\qquad w_1x_1+w_2x_2>\theta\\ \end{matrix} \right. y=⎩⎨⎧0w1x1+w2x2≤θ1w1x1+w2x2>θ
如图所示为：
感知机的多个输入信号都有各自固有的权重，这些权重发挥着控制各个信号的重要性作用。也就是说，权重越大，对应该权重的信号的重要性就越高。
二、简单的逻辑电路
1、与门
与门是有两个输入和一个输出的门电路，如图所示，与门仅在两个输入为1时输出为1，其他时候输出为0.
| x 1 x_1 x1 | x 2 x_2 x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
2、或门
或门是只要是一个输入信号是1，输出的结果就是1的逻辑电路。
| x 1 x_1 x1 | x 2 x_2 x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
3、与非门
与非门就是颠倒了与门的输出，仅当 x 1 x_1 x1和 x 2 x_2 x2同时输出为1时输出为0，其他时候则输出为1.
| x 1 x_1 x1 | x 2 x_2 x2 | y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
三、感知机的实现
简单实现
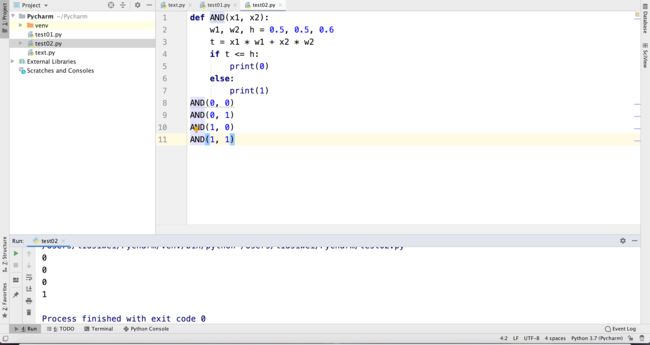
1、与门
def AND(x1, x2):
w1, w2, h = 0.5, 0.5, 0.6
t = x1 * w1 + x2 * w2
if t <= h:
print(0)
else:
print(1)
AND(0, 0)
AND(0, 1)
AND(1, 0)
AND(1, 1)
输出结果为：
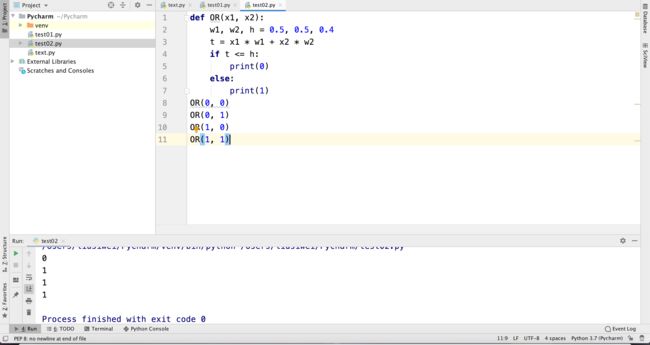
2、或门
def OR(x1, x2):
w1, w2, h = 0.5, 0.5, 0.4
t = x1 * w1 + x2 * w2
if t <= h:
print(0)
else:
print(1)
OR(0, 0)
OR(0, 1)
OR(1, 0)
OR(1, 1)
输出结果为：
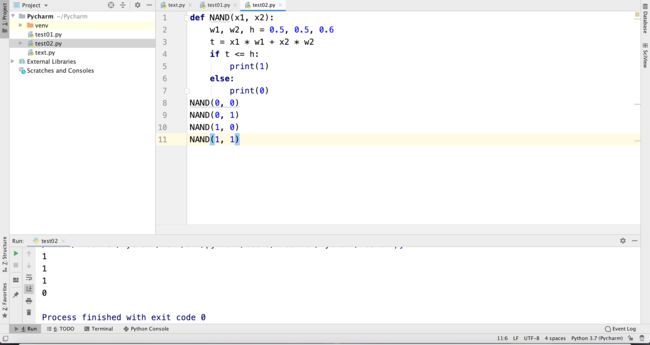
3、与非门
def NAND(x1, x2):
w1, w2, h = 0.5, 0.5, 0.6
t = x1 * w1 + x2 * w2
if t <= h:
print(1)
else:
print(0)
NAND(0, 0)
NAND(0, 1)
NAND(1, 0)
NAND(1, 1)
输出结果为：
导入权重和偏置
刚才的逻辑电路实现比较直接，容易理解。我们将上式修改为另一种形式，将上式的 θ \theta θ修改为 − b -b −b。可表示为：
y = { 0 b + w 1 x 1 + w 2 x 2 ≤ 0 1 b + w 1 x 1 + w 2 x 2 > 0 y=\left\{ \begin{matrix}0\qquad b+w_1x_1+w_2x_2\leq0 \\ \\ 1\qquad b+w_1x_1+w_2x_2>0\\ \end{matrix} \right. y=⎩⎨⎧0b+w1x1+w2x2≤01b+w1x1+w2x2>0
两个式子虽然有些符号不同，但是表达的内容完全一样，此处， b b b称为偏置， w 1 w_1 w1 w 2 w_2 w2称为权重。
感知机会计算输入信号和权重的乘积，然后再加上偏置，如果这个值大于0则输出1；否则输出0。
1、与门
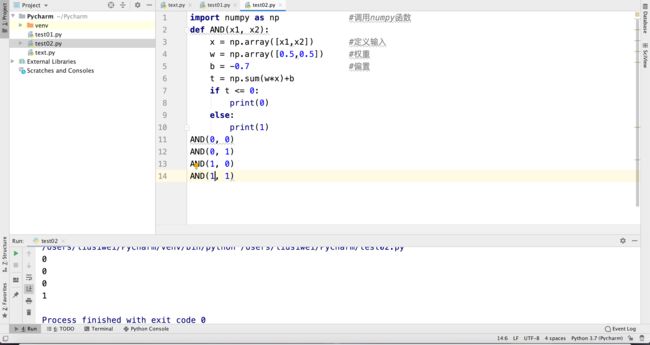
import numpy as np #调用numpy函数
def AND(x1, x2):
x = np.array([x1,x2]) #定义输入
w = np.array([0.5,0.5]) #权重
b = -0.7 #偏置
t = np.sum(w*x)+b
if t <= 0:
print(0)
else:
print(1)
AND(0, 0)
AND(0, 1)
AND(1, 0)
AND(1, 1)
输出结果为：
2、或门
import numpy as np #调用numpy函数
def OR(x1, x2):
x = np.array([x1,x2]) #定义输入
w = np.array([0.5,0.5]) #权重
b = -0.2 #偏置
t = np.sum(w*x)+b
if t <= 0:
print(0)
else:
print(1)
OR(0, 0)
OR(0, 1)
OR(1, 0)
OR(1, 1)
输出结果为：
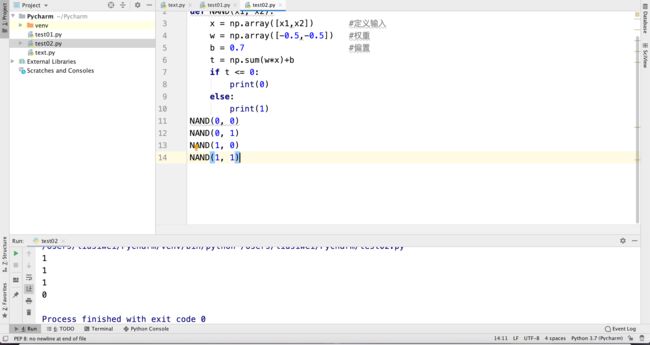
3、与非门
import numpy as np #调用numpy函数
def NAND(x1, x2):
x = np.array([x1,x2]) #定义输入
w = np.array([-0.5,-0.5]) #权重
b = 0.7 #偏置
t = np.sum(w*x)+b
if t <= 0:
print(0)
else:
print(1)
NAND(0, 0)
NAND(0, 1)
NAND(1, 0)
NAND(1, 1)
输出结果为：
