算法工程师的数学基础｜微积分之微分相关介绍

【算法工程师的数学基础】系列将会从线性代数、微积分、数值优化、概率论、信息论五个方面进行介绍，感兴趣的欢迎关注【搜索与推荐Wiki】公众号，获得最新文章。

《算法工程师的数学基础》已更新：

• 1、算法工程师的数学基础｜线性代数中的向量和向量空间
• 2、算法工程师的数学基础｜线性代数中的矩阵
• 3、算法工程师的数学基础｜微积分之导数相关介绍
• 4、算法工程师的数学基础｜微积分之微分相关介绍

接下来将会有两篇文章分别介绍下微积分中的微分和积分，内容来自网上公开资料、相关书籍和个人见解。

微积分 是对无穷小量的研究。无穷小量，简单说就是大小无限趋向于 0 的量， 很多整体分析太过复杂的物理量可以用无穷小量分析，其原因是无穷小量可以被线性化。

如果我们用 $ϵ$ 来表示无穷小量，那么微积分可以被分为两大类，微分和积分。

• 微分主要研究两个无穷小量的比值，形如 $\frac{{ϵ}_1}{{ϵ}_2}$
• 积分学主要研究无限多的无穷小量之和，也就是 ${ϵ}_1+{ϵ}_2+{ϵ}_3+...=\underset{n\to \infty }{\lim }{\sum }_{k=1}^n{ϵ}_k$

本篇主要介绍微分！内容注重理解微分的概念和与导数的区别，不像导数篇中那样用公式贯穿全文！

---

导数与线性化

微积分之所以在数学、物理学和工程学中有如此重要的地位，是因为在这些学科中有很多情况不好直接分析，而通过微积分可以把这些情况线性化。然而，在线性化的同时，研究对象就会变成无穷小量。

eg 1：一个正方形金属薄片受热后面积的改变量

设边长由 $x_0$ 变成 $x_0+\Delta x$，则正方形的面积由$x_0^2$ 变成 $(x_0+\Delta x{)}^2$，那么面积之差为：
$$\begin{gathered} \Delta A=(x_0+\Delta x{)}^2-x_0^2 \\ =2x_0\Delta x+(\Delta x{)}^2 \end{gathered}$$

上式中

• 加号左侧为 $\Delta x$的线性部分，且为$\Delta A$的主要组成部分
• 加号右侧为 $\Delta x$的高阶无穷小，当$\Delta x$很小时，可以忽略

从上面的例子中，可以看出函数线性化的那么一丁点意思了，接着看另外一个例子。

eg 2：假设一辆正在行驶的汽车，其走过的路程与时间满足关系 $x(t)=t^2$，那么在$t=1$时刻，如何知道他的速度？

由于平均速度$v=\frac{\Delta x}{\Delta t}=\frac{x_1-x_0}{t_1-t_0}$，带入 $t_0=1$得到从时刻$1\to t$的平均速度为：
$$\frac{x(t)-x(1)}{t-1}$$

如果让 $t=1.1$，那么这个平均速度就很接近$t=1$这一时刻的瞬间速度了。那么有理由相信在 $t$无限接近于1时，这个平均速度就很接近$t$时刻的瞬间速度了。

从平均速度的定义来看，从$1\to t$的平均速度等价于连接$(1,1)$ 和 $(t,t^2)$两点直线的斜率，所以当 $t$越来越接近于1的时候，这条直线的斜率就变成了在$(1,1)$切线的斜率。

而从导数的概念可以知道，函数在某点的斜率等于改点的导数，结合 eg 2可知
$$f^{\prime }(t)=2t=\frac{\Delta y}{\Delta x}$$
$$\Rightarrow \Delta y=2t\Delta x$$

和 eg 1中，当 $\Delta x$趋向于无穷小时的表达式是一样的，我们可以认为 $\Delta y$是关于$\Delta x$的线性化函数。

微分的定义

设函数$y=f(x)$在某区间内有定义，且 $x_0$ 及 $x_0+\Delta x$在这区间内，如果下面的公式成立（其中$A$是与$\Delta$无关的常数），则称 $y=f(x)$在点$x_0$处可微，并且称$A\Delta x$为函数$y=f(x)$ 在点$x_0$相应于自变量增量$\Delta x$的微分，计作：$dy{|}_{x=x_0}$ 或 $df(x_0)$，即：$dy{|}_{x=x_0}=A\Delta x$

$$\Delta y=f(x_0+\Delta x)-f(x_0)=A\Delta x+o(\Delta x_0)$$

微分$dy$ 叫做函数增量$\Delta y$的线性主部。这也是微分的实质：微分 本质是一个微小的线性变化量，用一个线性函数作为原函数变化的逼近。

由上面的定义可知：

• $dy$是自变量的改变量$\Delta x$的线性函数
• $\Delta y-dy=o(\Delta x)$是比$\Delta x$的高阶无穷小
• 当$A\ne 0$时，$dy$与$\Delta y$是等价无穷小，因为：$\frac{\Delta y}{dy}=1+\frac{o(\Delta x)}{dy}\to 1(\Delta x\to 0)$
• $A$是与$\Delta x$无关的常数，但与$f(x)$和$x_0$有关
• 当$\Delta x$很小时，$\Delta y\approx dy$（线性主部）

从微分的定义中也可以看出微分和导数的最大区别为：导数是指函数在某一点变化的快慢，是一种变化率；微分是指函数在某一点处的变化量，是一种变化的量。

基本初等函数的微分公式和运算法则

微分公式

$cotx$ ：余切函数，$cotx=\frac{1}{tanx}$

$secx$ ：正割函数，$secx=\frac{1}{cosx}$

$cscx$ ：余割函数，$cscx=\frac{1}{sinx}$

$$d(C)=0$$
$$d(x^{\mu })=\mu x^{\mu -1}dx$$
$$\begin{gathered} d(sinx)=cosxdx \\ d(cosx)=-sinxdx \\ d(tanx)=se{c}^{2}xdx \\ d(cotx)=-cscxdx \\ d(secx)=secxtanxdx \\ d(cscx)=-cscxcotxdx \end{gathered}$$
$$d(a^x)=a^{x}lnadx$$
$$d(e^x)=e^{x}dx$$
$$d(lo{g}_{a}x)=\frac{1}{lna}dx$$
$$d(lnx)=\frac{1}{x}dx$$
$$d(arcsinx)=\frac{1}{\sqrt{1-x^2}}dx$$
$$d(arccosx)=-\frac{1}{\sqrt{1-x^2}}dx$$
$$d(arctanx)=\frac{1}{1+x^2}dx$$
$$d(arccotx)=-\frac{1}{1+x^2}dx$$

运算法则

$$d(u\pm v)=d(u)\pm d(v)$$
$$d(Cu)=Cd(u)$$
$$d(uv)=vd(u)+ud(v)$$
$$d(\frac{u}{v})=\frac{vd(u)-ud(v)}{v^2}$$

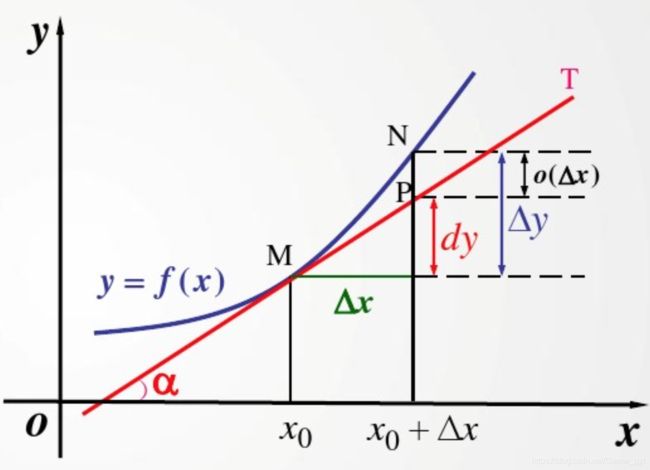
微分的几何意义

当$\Delta y$是曲线的纵坐标的增量时，$dy$ 是切线纵坐标对应的增量，当$\Delta x$很小时，在点$M$附近，切线段$MP$可近似代替曲线段$MN$

在局部范围内用线性函数近似代替非线性函数，在几何上就是局部用切线段代替曲线段，这在数学上称之为非线性函数的局部线性化，这就是微分学的基本思想之一。

微分在近似计算中的应用

微分近似计算的理论基础

当$\Delta x$很小时

$$\Delta y\approx dy=f^{\prime }(x_0)\Delta x$$
上面的公式也可以写为：
$$\Delta y=f(x_0+\Delta x)-f(x_0)\approx f^{\prime }(x_0)\Delta x$$
或
$$f(x_0+\Delta x)=f(x_0)+f^{\prime }(x_0)\Delta x$$
将上式中的 $x_0+\Delta x$ 用 $x$代替，则可以改写为：
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)$$

常见的近似计算的基本公式

$$\sqrt[n]{1+x}\approx +\frac{1}{n}x$$
$$sinx\approx x$$

$$tanx\approx x$$

$$e^x\approx 1+x$$

$$ln(1+x)\approx x$$

微分中值定理和导数的应用

费马引理

设 函数f(x)在点 $x_0$的某邻域$U(x_0)$内有定义，并且再$x_0$处可导，如果对任意的$x\in U(x_0)$有：$f(x)⩽f(x_0)$ 或 $f(x)⩾f(x_0)$，那么$f^{\prime }(x_0)=0$

罗尔定理

如果函数$f(x)$满足

• 在闭区间$[a,b]$上连续
• 在开区间$(a,b)$内可导
• 在区间端点处的函数值相等，即$f(a)=f(b)$

那么$(a,b)$上至少有一点$\epsilon (a<\epsilon <b)$使得$f^{\prime }(\epsilon )=0$。

拉格朗日中值定理

如果函数$f(x)$满足：

• 在闭区间$[a,b]$上连续
• 在开区间$(a,b)$内可导
  那么在$(a,b)$内至少有一点$\epsilon (a<\epsilon <b)$使得$f(b)-f(a)=f^{\prime }(\epsilon )(b-a)$成立。

柯西中值定理

如果函数$f(x)$及$F(x)$满足：

• 在闭区间$[a,b]$上连续
• 在开区间$(a,b)$内可导
• 对任一 $x\in (a,b),F^{\prime }(x)\ne 0$

那么在$(a,b)$内至少有一点$\epsilon$，使下面等式成立。
$$\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f^{\prime }(\epsilon )}{F^{\prime }(\epsilon )}$$

洛必达法则

设：

• 当$x->a$时，函数$f(x)$及$F(x)$都趋向于零
• 在点$a$的某去心邻域内，$f^{\prime }(x)$及$F^{\prime }(x)$都存在且$F^{\prime }(x)\ne 0$
• ${\lim }_{x\to a}\frac{f(x)}{F(x)}$存在（或为无穷大）
  那么：
  $$\underset{x\to a}{\lim }\frac{f(x)}{F(x)}=\underset{x\to a}{\lim }\frac{f^{\prime }(x)}{F^{\prime }(x)}$$

这种在一定条件下通过分子分母分别求导再求导极限来确定未定式的值的方法称为洛必达法则。

泰勒中值定理

如果函数$f(x)$在含有$x_0$的某个开区间$(a,b)$内具有直到$(n+1)$阶的导数，则对任一$x\in (a,b)$，有：
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+...+\frac{f^n(x_0)}{n!}(x-x_0{)}^n+R_n(x)$$
其中
$$R_n(x)=\frac{f^{n+1}(\epsilon )}{(n+1)!}(x-x_0{)}^{n+1}$$
这里$\epsilon$为 $x_0$和$x$之间的某个值。

上述公式中$f(x)$表达式为 $f(x)$按$(x-x_0)$的幂展开的带有拉格朗日型余项的$n$阶泰勒公式，$R_n(x)$的表达式称为拉格朗日型余项。

---

OK，关于微积分中的微分部分已经介绍完毕！期待下篇的积分吧！

---

参考资料

• https://blog.csdn.net/weixin_40163242/article/details/89004822
• https://www.zhihu.com/question/336322284
• https://www.zhihu.com/question/264955988?sort=created

---

扫一扫 关注微信公众号！号主 专注于搜索和推荐系统，尝试使用算法去更好的服务于用户，包括但不局限于机器学习，深度学习，强化学习，自然语言理解，知识图谱，还不定时分享技术，资料，思考等文章！

---