CS231n: (3) Loss Functions and Optimization

问答总结:

• 损失函数的产生原因是什么，它的定义是什么?

• 多类别SVM损失函数的定义是什么? 有什么实际意义?

• 多类别SVM损失函数为什么以1为间隔阈值?以其他为阈值有影响吗?

• 对于多类别SVM损失函数，我们初始化$W$非常小，那么$s\approx 0$, 则初始的损失应该为多少?

  C-1(C为类别数量)

• 为什么说多类别SVM损失函数中，任何缩放操作都不会有影响?(个人理解, 待探究)

  (1) 在分类问题中: 本质上我们只在乎真实类别的分数要高于其他类别，高多少无所谓.
  (2) 线性分类器中，模型参数成倍缩放并不改变超平面。

• 如何从几何直观，样本空间和贝叶斯角度理解正则化。常见的$L_1$和$L_2$正则化有什么特点?

• 使用softmax分类器的过程是怎样的? 我们初始化$W$非常小，那么$s\approx 0$, 则初始的损失应该为多少?

  先使用softmax将分数转换为概率分布，然后使用最大似然思想定义损失函数。最开始时，每个类别概率相同，为$\frac{1}{C}$, 故损失为logC.

• 多类别SVM损失函数和softmax损失函数的区别是什么?

• 梯度的定义是什么，几何意义是什么?计算的方式有哪两种?

• 随机梯度下降是什么？为什么会有随机梯度下降算法?

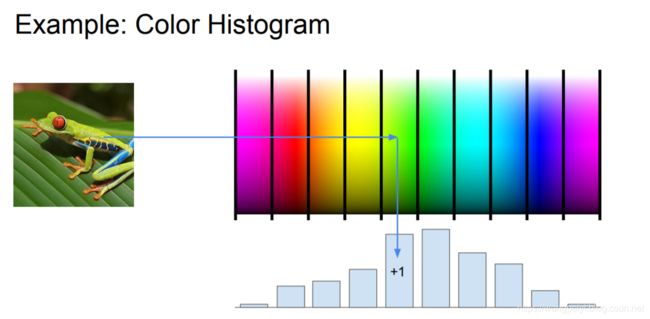
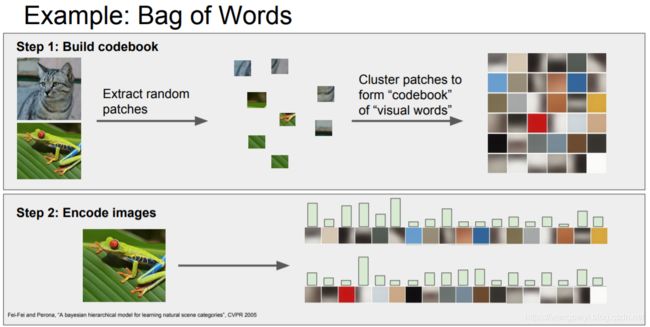
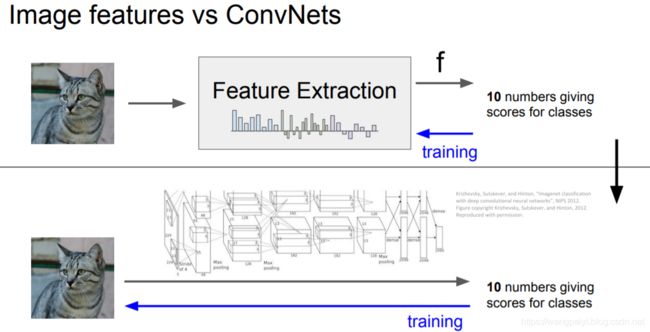
• 图像领域的基本的特征提取方法有哪些?早期基于特征工程和现在基于深度学习方法的区别是什么?

---

一、损失函数

1、来源与定义

为了让算法能够衡量模型的表现，因此我们提出了损失函数的概念。在一个数据集上的损失函数是所有样本损失的平均。定义如下:
$$L=\frac{1}{N}\sum _i{L}_i(f(x_i,W),y_i)$$.
其中$\{x_i,y_i{\}}_{i=1}^N$为训练集，$f$为模型，$W$为模型参数。

2、多类别SVM损失函数

定义多类别SVM损失函数如下:
$$\begin{array}{rl}{L}_i& =\sum _{j!=y_i}\{\begin{array}{ll}0& s_{y_i}-s_j-1\ge 0\\ -(s_{y_i}-s_j-1)& else\end{array}\\ & =\sum _{j!=y_i}max(0,-(s_{y_i}-s_j-1))\end{array}$$

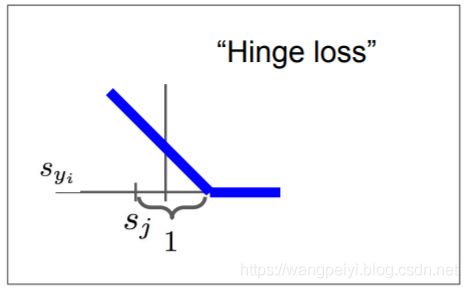
这个式子的意义是说: 对一个样本，要没有损失，那么它所属类别的得分必须至少比其他类别的得分高1.，至于为什么是高1, 因为这里的阈值1和二分类SVM中的函数间隔相似，我们可以通过缩放分类器中的参数$W\to \lambda W$, $b\to \lambda b$，将阈值固定为1，而不影响优化结果。因此这只是一个为了简单而选择的阈值，选择其他大于0的阈值也可以。

---

个人疑惑: SVM本质上是要最大化样本点和超平面的几何间隔。缩放超平面系数不会改变超平面，因此可以将函数间隔设定为1. 从而简化优化目标。

但是，在多类别SVM损失函数中，似乎并没有体现SVM的思想，因为根本就没有最大化间隔的概念，它的核心思想就是正确类别的分数应该大于其他类别，然后莫名其妙定义了一个阈值1。如果是这样，损失函数定义为：
$$L_i=\sum _{j!=y_i}\{\begin{array}{ll}0& s_{y_i}-s_j>0\\ -(s_{y_i}-s_j)& else\end{array}$$
岂不是更简单.难道只是为了写代码方便才按上方这样定义损失函数吗。。

• (1) 为什么要像课件那样定义损失函数呢?
• (2) 为什么要叫做多类别SVM损失损失函数呢?

个人理解：
(1) 如果是定义为第二种损失函数，是没有办法处理$s_{y_i}=s_j$的情况的，因此需要给定一个间隔阈值，线性分类器本质上也是找高维空间分类平面，因此参数可以缩放，所以间隔可以任意给定，可能是为了简单，给了个1.
(2) 类别分数的计算是这样的 $s_i=w_{i}x+b_i$, 这个可以看做样本距类别$i$的超平面的有向间隔，有向间隔越大说明越可能在这个类别中。那么$s_{y_i}-s_i$就可以看做是正确类别和错误类别的相对有向间隔，因此问题转化为尽量使得相对有向间隔大于阈值，因此叫做多类别SVM损失函数。但是个人认为，就损失函数来看，多类别SVM损失函数并没有像SVM那样，找到了最安全的多个超平面.

---

3、softmax+最大似然损失函数

softmax classifier也叫多项逻辑回归。当分类器输出每个类别分数后。用$\mathbf{s}\in R^C$表示分数向量. 我们对其进行归一化，使其变为一个概率分布:
$$P(Y=k|X=x_i;\theta )=\frac{e^{s_k}}{{\sum }_j{e}^{s_j}}$$
其中$\theta$为模型参数，然后由最大似然思想，我们需要求解下式:
$$\begin{array}{rl}arg\underset{\theta }{\max }{\Pi }_i^{N}p(y_i|x_i;\theta )& =-arg\underset{\theta }{\min }{\Pi }_i^{N}p(y_i|x_i;\theta )\\ & =-arg\underset{\theta }{\min }\sum _i^{N}log(p(y_i|x_i;\theta ))\end{array}$$

4、两个损失函数的区别

• 多类别SVM损失函数：当得分超过某个阈值边放弃优化，见好就收。
• softmax损失函数：不断将概率质量向正确类别聚集，永无止境

在实践中，并不会有很大差距。

二、正则化

使用函数去拟合数据的过程中，有很重要的问题就是过拟合。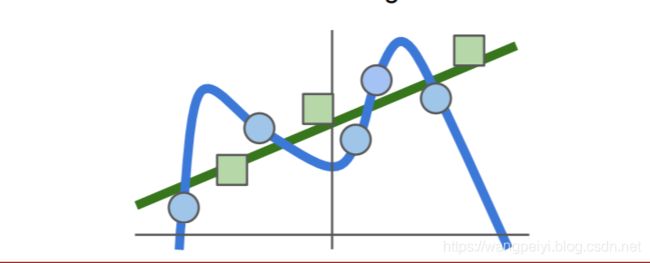
如图所示，蓝线表示的函数过拟合了，好的函数应该是绿色。如何将蓝色的线变为绿色。我们有两种方式。
(1)直接规定用最高次为1次的函数去拟合数据。
(2)使用高次函数拟合数据，但是增加正则项，以使得曲线接近绿色。

当然正则化不止是添加正则项, 常见的正则化方式有: (1) 添加正则项。(2)使用Dropout(神经网络中)。(3)Batch normalization等

三、优化

1、寻找方向：梯度

定义了损失函数，那么我们要如何得到最小化损失函数的模型参数呢?这就是一个优化问题了。
为了描述问题的直观性，我们假定模型参数只有两个变量。那么损失函数可以看作三维空间里的平面。

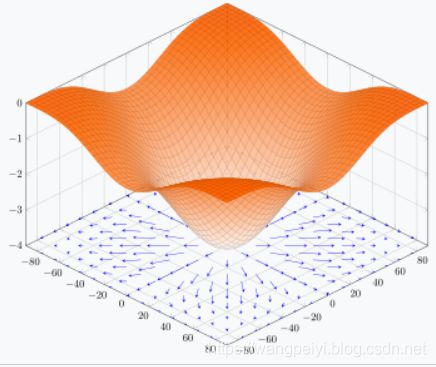
我们优化的目标就是尽可能到达更低的点，更形象地，就是下山地过程。那么，往哪个方向下山呢? 我们知道多元函数的梯度总是指向坡度最陡的方向，那么我们要下山，就沿负梯度方向行走。因此要下山，关键靠梯度指路。

2、梯度计算

多元函数梯度定义如下
$$\nabla f(x,y)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$$
根据偏导数的定义, $f(x,y)$在点(a, b)关于$x$的偏导数为:
$$\frac{\partial f}{\partial x}=\underset{h\to 0}{\lim }\frac{f(a+h,b)-f(a,b)}{h}$$
由此差商定义，我们得到基本的:
(1) 数值计算法: 选取一个小的$h$比如0.00001，然后依次计算每个变量的偏导数，最终得到梯度。

由于数值计算法需要循环计算，计算量巨大，但是根据基本定义，我们能够推导出很多求导公式和法则，因此有
(2)直接计算法: 由相应公式直接求得梯度表达式，其间涉及到矩阵求导，然后直接由表达式快速计算梯度。

验证: 我们常常使用第一个方法作为第二个方法的测试单元，以确定我们求得的梯度表达式正确。

3、梯度下降与随机梯度下降

(1) 梯度下降

得到梯度，我们就找到了方向。这样我们随机初始化一个起始点weights，然后根据损失函数计算梯度weight_grad，设定超参数step_size, 然后更新。基本的代码框架如下:

(2) 随机梯度下降
但是很明显，对于损失函数:
$$L(W)=\frac{1}{N}\sum _{i=1}^N{L}_i(x_i,y_i;W)+\lambda R(W)$$
其梯度为:
$${\nabla }_{W}L(W)=\frac{1}{N}\sum _{i=1}^N{\nabla }_W{L}_i(x_i,y_i;W)+\lambda {\nabla }_{W}R(W)$$
要计算梯度，需要遍历整个数据集，这需要消耗大量的计算力。更具采样的思想，提出随机梯度下降(SGD) 算法。我们每次抽样一个batch的样本，以此代表整体，求得梯度，然后更新。这本质上也是一种计算力和方向准确度的折中。代码框架如下。

• 一个演示梯度更新的Demo

特征工程

1、思想

直接将图像的像素点放进分类器，效果可能不尽如人意，因此我们可能先根据人的经验，从图像中抽取一些特征。然后将特征放入分类器。这样的本质思想是：特征空间的变换。一个直观的例子如下：

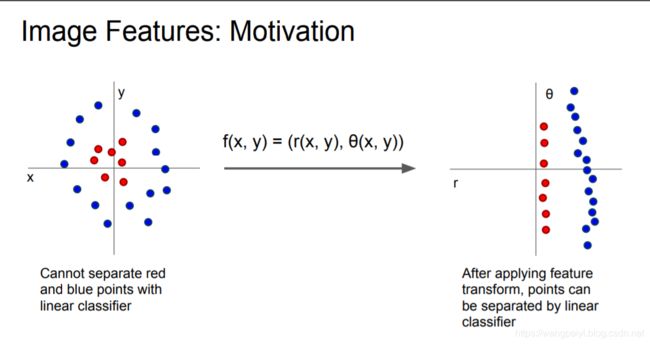
将特征从$(x,y)$(笛卡尔坐标系)转换为$(p,\theta )$(极坐标系). 从而将数据集变为线性可分。

2、方法

在图像领域，常见的特征提取方法有:
(1): 色彩直方图:

(2): 图像的方向梯度

(3) 词袋模型演变

不过在进入深度学习时代后，基本可以省去特征工程，将特征交给模型去学习了。