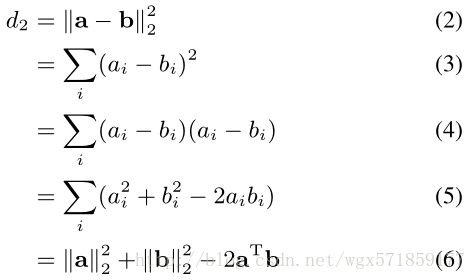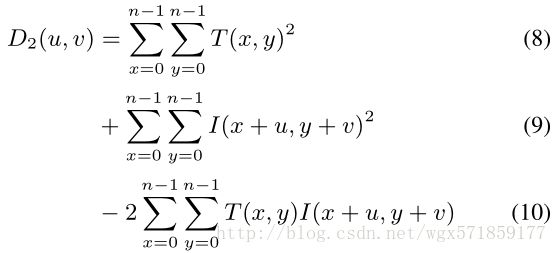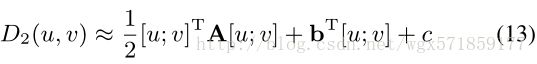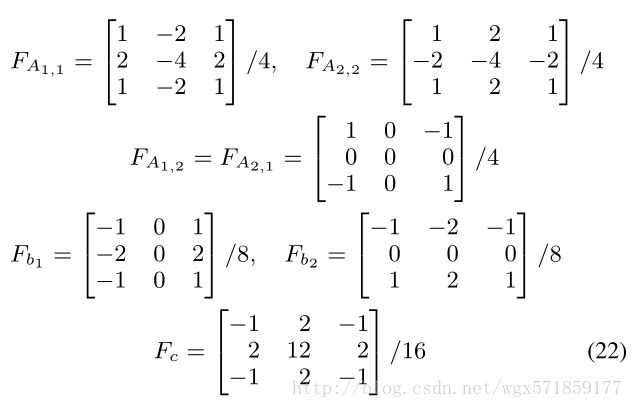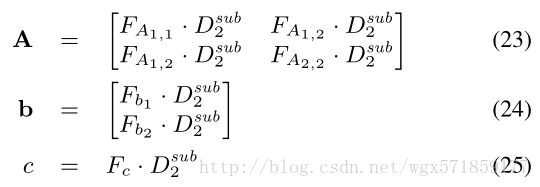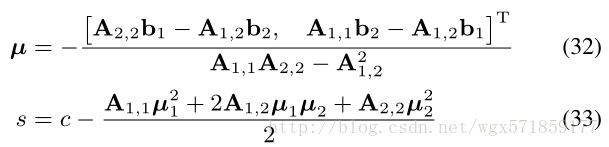谷歌HDR+研读（四）附加材料

paper:

Burst photography for high dynamic range and low-light imaging on mobile cameras Supplemental Material

谷歌翻译如下：

1蛮力L1对齐

在我们粗略精细对齐策略的最佳范围内，我们需要一种对齐技术，该技术在给定大块尺寸但非常小的搜索半径的情况下性能良好。在这种情况下，诸如我们之前描述的快速子像素L2对准的技术或者甚至诸如相位相关的简单技术（Kuglin和Hines 1975）都被执行良好的暴力程序胜过，其使绝对残差最小化。我们使用绝对残差而不是平方残差，因为它们很好地映射到低级计算机体系结构。与平方残差相比，相同输入数据的绝对残差需要更少的位数，从而实现更高的吞吐量。在ARM体系结构中，实际上存在一种计算绝对差异然后累积的操作，使得L1距离的蛮力计算非常计算地轻。该方法通过搜索半径的二次方进行缩放，使其在搜索半径较小的情况下最具吸引力。

2图像对齐金字塔

我们用于对齐的图像金字塔被构造为平衡计算工作量和对齐结果的质量。我们对质量和计算的主要控制是我们在每个金字塔等级搜索的距离。较大的搜索距离允许在金字塔等级之间有较大的下采样因子，这降低了搜索陷入局部最小值的可能性。一般来说，较大的搜索距离是不切实际的;然而，本文介绍的快速L2范数搜索使我们能够使用±4像素的相对较大的搜索区域。然而，尽管快速L2范数搜索在算法上是高效的，但它仍然比较小区域的简单搜索要慢。因此，我们对底部（高分辨率）金字塔等级使用±1像素的L1搜索（第1部分）。

将所有这些放在一起，我们管道中的典型对齐金字塔将如下所示：
•金字塔底层，将拜耳下采样为灰度。该金字塔等级使用L1对齐算法使用±1像素搜索，使用大小为16×16的块。

•由于底部金字塔等级使用±1像素搜索，因此此金字塔等级可以从底层向下采样2倍。此金字塔等级使用快速L2对齐算法进行±4像素搜索，使用大小为16的瓦片×16。

•由于前一级使用±4像素搜索，因此可以将该金字塔级降采样4倍。再次，这个pyra-level级使用快速L2对齐算法的±4像素搜索，使用大小为16× 16。

•最后一级与上一级相似;它以4的因子下采样，并使用相同的搜索算法。然而，在这一点上，我们已经下采样了很多，以致在原始图像中16×16的图块大小实际上非常大。覆盖原始图像中较大有效区域的瓦片有助于减少噪音对搜索的影响，并避免局部最小值。然而，大块瓷砖开始无法逼近非严格平移的场景运动。同时，足够大的瓷砖很大程度上消除了噪音对结果的影响。因此，我们将拼贴大小减少到8×8。

3快速L2残差计算

首先，让我们解决拍摄两个小的子图像和计算“距离图像”的问题，该距离图像测量图像的所有可能的偏移（平移）的两个子图像之间的不匹配。实际上，这将告诉我们两个图像的所有可能的平移的相对好处，我们的假设是使我们的距离测量最小化的平移是对将第一子图像转换为第二子图像的运动的良好估计。

首先，让我们以一个简化的案例开始我们的推导。考虑计算两个向量a和b之间的平方L2距离的问题：

这个距离可以通过重新组织数学来重写：

我们看到两个向量之间的平方L2距离解耦成每个向量的平方L2范数，减去两个向量的内积的两倍。

现在让我们考虑一个n×n图像模板T和一个m×m图像I，其中m> n。也就是说，我们有一些大的图像，我们有一个图像模板，我们想要比较每个n×n 图像的子图像。我们会假设我们的图像和模板为了方便起见而是灰度的，尽管我们的方法可以泛化为彩色图像。更正式地说，我们想要计算 a（m-n + 1）×（m-n + 1）“距离图像”D2，使得：

 

有关模板，图像和距离图像的示例，请参见图2。

图2：通过计算小图像模板（a）和较大图像（b）的每个可能的匹配子图像之间的平方残差产生的距离表面（c）的可视化。

和以前一样，这个距离计算可以简化：

第一项只取决于T而不取决于u和v，因此它可以计算一次并在计算D2（u，v）所有值时重新使用。第二项可以通过盒式滤波I（x，y）2计算（u，v）的所有值，这可以使用滑动窗口图像滤波技术，或使用积分图像（效率稍低）。第三项也可以通过互相关I和T来计算（u，v）的所有值。互相关计算成本可能很昂贵，但可以使用快速傅立叶变换大大加快。从卷积定理，我们知道：

其中F {•}是傅立叶变换，F -1 {•}是傅立叶逆变换，◦是两个矢量的乘积（Hadamard乘积），F {a} *是F {a}的共轭转置。这个会从一维信号推广到二维图像。

有了这三个观察，我们可以重写所有可能的偏移（u，v）的距离“图像”D2的计算：

其中第一项是T的平方元素之和，第二项是图像I的平方元素，用大小为n×n的盒式过滤器过滤（其中箱式过滤器未被归一化），第三项是 - 2×I和T的互相关，使用快速傅里叶变换有效地计算。

4亚像素精确翻译

给定距离图像D2（u，v），我们希望通过定位D2的最小值来找到T和I之间的单个最佳匹配。为了产生亚像素精度的平移估计，我们将使用一个二元二次函数（二维多项式），它适合于D2的每像素最小值附近。这种方法比拟合两个可分离函数的标准方法产生更高质量的翻译估计[Stone et al。 2001]，因为它共同估计两维的最小值，而不是独立估计每个维度的最小值，在轴的情况下会产生更准确的结果 D2（u，v）在u和v中不是各向同性的，这在实践中很少见（见图2c）。更正式地说，我们将D2近似为
如下：

其中A是2×2正半定矩阵，b是2×1向量，c是标量。 A被认为是PSD，因为我们预计D2在最小值附近的形状是一个向上的二次方
表面，而不是鞍形或面向下的表面。令（u，v）为D2中具有最小距离值的像素的坐标。我们将在（u，v）周围考虑3×3像素区域

拟合我们的二次函数：

当拟合我们的二元多项式时，我们将根据3×3大小的二项式权重块对最小值附近的像素进行加权：

使用Dsub和W，我们可以在我们的二次近似（A，b，c）中针对自由参数设置最小二乘问题并解决它。不失一般性，我们将求解一个假设中心像素具有（u，v）坐标为（0,0）的Dsub，然后将我们将估计的子像素位置移动（u， v）。
为了构造我们的最小二乘问题，我们必须首先构造一个矩阵X包含我们的3×3补丁中的9（u，v）坐标的二阶多项式展开式：

我们将另外根据等式15中的（矢量化的）3×3权重“图像”构建对角“权重”矩阵，并且将RHS矢量 y作为Dsub的矢量化版本：

用这些我们可以构造一个最小二乘问题，它对应于拟合我们的二元多项式：

 

这是一个传统的加权最小二乘问题，所以可以用各种方法解决。理想情况下，我们希望避免重复求解我们对齐中每个瓦片的线性方程组。通过利用X和W在所有瓷砖上不变的事实，可以显着加快这种重复的拟合。因此，我们可以重新排列我们的线性系统，使得多项式拟合参数β是图像块y和固定矩阵F的线性函数：

由此我们可以看出，我们可以通过简单地将y的内积（矢量化的D2的3×3图像片）乘以F的每一行来计算双变量多项式的参数。该矩阵F相当于滤波器银行，每个过滤器对应于（A，b，c）中的某个未知参数：

使用这些滤波器，我们可以通过简单地取Dsub的内积来估计我们的二次近似的自由参数

这些滤波器（假设误差曲面和滤波器已被矢量化），或等效地通过计算Dsub与这些滤波器的互相关：

这个过程类似于[Farneba¨ck2002]的多项式展开法。常数移位c及其滤波器F与我们的亚像素最小定位无关，但为了完整起见，这里包括在内。
根据Dsub的形状，与我们的初始假设相反，估计的A可能不是半确定的。为了解决这个问题，在估计了二次方的参数之后，我们首先强制A的对角元素为非负：

然后我们计算A的行列式

如果det（A）<0，那么我们将A的非对角元素设置为零。这些修正给了我们一个肯定是半确定的答案。

利用我们的二次近似，我们现在可以估计该二次方的最小值。这样做需要我们通过完成平方以不同的形式重写我们的二次方程：

 

给定一个在第一种形式中定义的二次方程式，我们可以将其转换为第二种形式如下：

对于我们特定的二元情况，这相当于：

一旦我们恢复了二次μ的最小值的位置，我们可以简单地将其作为最小值的子像素位置。请注意，我们生成的拟合曲面将D2的中心像素视为（0,0），因此在拟合之后，我们需要将每个像素的最小位置（u，v）添加到μ中，这使我们得到了最小值的实际位置在D2中。在存在严重噪声或非常平坦的图像时，预测的子像素最小值μ可能与观察到的每像素最小值（u，v）非常不同，所以在

如果我们观察到两者足够不同（去掉多于1个像素），我们设置μ= [u; V]。