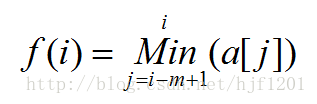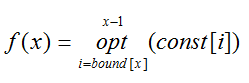动态规划之单调队列优化专题【附题目练习清单】
什么是单调(双端)队列
单调队列,顾名思义,就是一个元素单调的队列,那么就能保证队首的元素是最小(最大)的,从而满足动态规划的最优性问题的需求。
单调队列,又名双端队列。双端队列,就是说它不同于一般的队列只能在队首删除、队尾插入,它能够在队首、队尾同时进行删除。
【单调队列的性质】
一般,在动态规划的过程中,单调队列中每个元素一般存储的是两个值:
1.在原数列中的位置(下标)
2.他在动态规划中的状态值
而单调队列则保证这两个值同时单调。
【单调队列有什么用】
我们来看这样一个问题:一个含有n项的数列(n<=2000000),求出每一项前面的第m个数到它这个区间内的最小值。
这道题目,我们很容易想到线段树、或者st算法之类的RMQ问题的解法。但庞大的数据范围让这些对数级的算法没有生存的空间。我们先尝试用动态规划的方法。用代表第个数对应的答案,表示第个数,很容易写出状态转移方程:
这个方程,直接求解的复杂度是O(nm)的,甚至比线段树还差。这时候,单调队列就发挥了他的作用:
我们维护这样一个队列:队列中的每个元素有两个域{position,value},分别代表他在原队列中的位置和,我们随时保持这个队列中的元素两个域都单调递增。
那计算的时候,只要在队首不断删除,直到队首的position大于等于,那此时队首的value必定是的不二人选,因为队列是单调的!
我们看看怎样将 插入到队列中供别人决策:首先,要保证position单调递增,由于我们动态规划的过程总是由小到大(反之亦然),所以肯定在队尾插入。又因为要保证队列的value单调递增,所以将队尾元素不断删除,直到队尾元素小于。
【时间效率分析】
很明显的一点,由于每个元素最多出队一次、进队一次,所以时间复杂度是O(n)。用单调队列完美的解决了这一题。
【为什么要这么做】
我们来分析为什么要这样在队尾插入:为什么前面那些比大的数就这样无情的被枪毙了?我们来反问自己:他们活着有什么意义?!由于是随着单调递增的,所以对于存在j
我们再来分析为什么能够在队首不断删除,一句话:是随着单调递增的!
【一些总结】
对于这样一类动态规划问题,我们可以运用单调队列来解决:
其中bound[x]随着x单调不降,而const[i]则是可以根据i在常数时间内确定的唯一的常数。这类问题,一般用单调队列在很优美的时间内解决。
【Jzoj1771】烽火传递
【在线测试提交传送门】
【问题描述】
烽火台又称烽燧,是重要的军事防御设施,一般建在险要或交通要道上。一旦有敌情发生,白天燃烧柴草,定代价。 为了使情报准确地传递,在连续m个烽火台中至少要有一个发出信号。请计算总共最少花费多少代价,才能使敌军来袭之时,情报能在这两座城市之间准确传递。
【输入格式】
第一行:两个整数N,M。其中N表示烽火台的个数,M表示在连续m个烽火台中至少要有一个发出信号。 接下来N行,每行一个数Wi,表示第i个烽火台发出信号所需代价。
【输出格式】
一行,表示答案。
【输入样例1】
5 3 1 2 5 6 2
【输出样例1】
4
【解题思路】
设f[i]表示i必须选时最小代价。 初值: f[0]=0 f[1..n]=∞ 方程: f[i]=min(f[j])+w[i] 并且max(0,i-m)≤j<i 为什么j有这样的范围?如果j能更小,那么j~i这段区间中将有不符合条件的子区间,就会错。应保证不能有缝隙。 最后在f[n-m+1..n]中取最小值即答案 , 时间复杂度O(nm)
#include //将超出范围的队头删掉
f[i]=f[que[head]]+w[i];//转移(用队头)
while (head<=tail && f[que[tail]]>f[i])
--tail;//将不比它优的全部删掉
que[++tail]=i;//将它加进队尾
}
int ans=0x7f7f7f7f;
for (i=n-m+1;i<=n;++i)
ans=min(ans,f[i]);
printf("%d\n",ans);
}
【Tyvj1305】最大最大子序和
【在线测试提交传送门】
【问题描述】
输入一个长度为n的整数序列,从中找出一段不超过M的连续子序列,使得整个序列的和最大。 例如 1,-3,5,1,-2,3 当m=4时,S=5+1-2+3=7; 当m=2或m=3时,S=5+1=6。
【输入格式】
第一行两个数n,m; 第二行有n个数,要求在n个数找到最大子序和。
【输出格式】
一个数,数出他们的最大子序和。
【输入样例】
6 4 1 -3 5 1 -2 3
【输出样例】
7
【数据范围】
n,m≤300000;数列元素的绝对值≤1000。
【解题思路】
这是一个典型的动态规划题目,不难得出一个1D/1D方程:
f(i) = sum[i]-min{sum[k]|i-M≤k≤i}
由于方程是1D/1D的,所以我们不想只得出简单的Θ(n^2)算法。不难发现,此优化的难点是计算min{sum[i-M]..sum[i-1]}。在上面的链接中,我们成功的用Θ(nlgn)的算法解决了这个问题。但如果数据范围进一步扩大,运用st表解决就力不从心了。所以我们需要一种更高效的方法,即可以在Θ(n)的摊还时间内解决问题的单调队列。
单调队列(Monotone queue)是一种特殊的优先队列,提供了两个操作:插入,查询最小值(最大值)。它的特殊之处在于它插入的不是值,而是一个指针(key)(wiki原文:imposes the restriction that a key (item) may only be inserted if its priority is greater than that of the last key extracted from the queue)。所谓单调,指当一组数据的指针1..n(优先级为A1..An)插入单调队列Q时,队列中的指针是单调递增的,队列中指针的优先级也是单调的。因为这里要维护优先级的最小值,那么队列是单调减的,也说队列是单调减的。
查询最小值
由于优先级是单调减的,所以最小值一定是队尾元素。直接取队尾即可。
插入操作:
当一个数据指针i(优先级为Ai)插入单调队列Q时,方法如下:
1.如果队列已空或队头的优先级比Ai大,删除队头元素。
2.否则将i插入队头
比如说,一个优先队列已经有优先级分别为 {5,3,-2} 的三个元素,插入一个新元素,优先级为2,操作如下:
1.因为2 < 5,删除队头,{3,-2}
2.因为2 < 3,删除队头,{-2}
3.因为2 > -2,插入队头,{2,-2}
证明性质可以得到维护
证明指针的单调减 :由于插入指针i一定比已经在队列中所有元素大,所以指针是单调减的。
证明优先级的单调减:由于每次将优先级比Ai大的删除,只要原队列优先级是单调的,新队列一定是单调的。用循环不变式易证正确性。
为什么删除队头:直观的,指针比i小(靠左)而优先级比Ai大的数据没有希望成为任何一个需要的子序列中的最小值。这一点是我们使用优先队列的根本原因。
维护区间大小
当一串数据A1..Ak插入时,得到的最小值是A1..Ak的最小值。反观dp方程:
f(i) = sum[i]-min{sum[k]|i-M≤k≤i} 1
在这里,A = sum。对于f(i),我们需要的其实是Ai-M .. Ai的最小值,而不是所有已插入数据的最小值(A1..Ai-1)。所以必须维护区间大小,使队列中的元素严格处于Ai-M..Ai-1这一区间,或者说删去哪些A中过于靠前而违反题目条件的值。由于队列中指针是单调的,也就是靠左的指针大于靠右的,或者说在优先队列中靠左的值,在A中一定靠后;优先队列中靠右的值,在A中一定靠前。我们想要删除过于靠前的,只需要在优先队列中从右一直删除,直到最右边(队尾)的值符合条件。具体地:当队头指针p满足i-m≤p时。
形象地说,就是忍痛割爱删去哪些较好但是不符合题目限制的数据。
#include
#include 【Vijos1243】生产产品
【在线测试提交传送门】
时间限制:1S / 空间限制:256MB
【问题描述】
产品的生产需要M个步骤,每一个步骤都可以在N台机器中的任何一台完成,但生产的步骤必须严格按顺序执行。由于这N台机器的性能不同,它们完成每一个步骤的所需时间也不同。机器i完成第j个步骤的时间为T[i,j]。把半成品从一台机器上搬到另一台机器上也需要一定的时间K。同时,为了保证安全和产品的质量,每台机器最多只能连续完成产品的L个步骤。也就是说,如果有一台机器连续完成了产品的L个步骤,下一个步骤就必须换一台机器来完成。 请计算最短需要多长时间。
【输入格式】
第一行有四个整数M, N, K, L; 接下来N行,每行有M个整数。第I+1行的第J个整数为T[J,I]。
【输出格式】
输出只有一行,表示需要的最短时间。
【输入样例1】
3 2 0 2 2 2 3 1 3 1
【输出样例1】
4
【数据范围】
对于50%的数据,N≤5,L≤4,M≤10000 对于100%的数据,N≤5, L≤50000,M≤100000
【解题思路】
转移方程为: f[i][j]=min( f[t][p]+sum[j][i]-sum[p][j]) 化简后可以得到 f[i][j]=min( f[t][p]-sum[p][j])+sum[j][i] 对于每一个j考虑开一个单调队列优化 ,维护 t和f[t][p]-sum[p][j]单调递增。这样每次从队首取出符合要求的一个即可更新. q[a][x][0]表示队列中这个位置的的t q[a][x][1]表示这个位置的p 每次先更新所有的f[i][j]然后再更新所有的队列q[k]
#include
using namespace std;
const int N=100010,INF=2099999999;
int q[10][N][2],l[10],r[10];
int m,n,cost,L,sum[10][N],f[N][10],ans=INF;
int main(){
scanf("%d%d%d%d",&m,&n,&cost,&L);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) scanf("%d",&sum[i][j]),sum[i][j]+=sum[i][j-1];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) f[j][i]=INF;
for(int i=1;i<=n;i++) q[i][ r[i]++ ][0]=0;
for(int i=1;i<=m;i++){
for(int k=1;k<=n;k++){
while(l[k]0]>L) l[k]++;
int t=q[k][ l[k] ][0],p=q[k][ l[k] ][1];
f[i][k]=min(f[i][k],f[t][p]+sum[k][i]-sum[k][t]+cost);
}
for(int k=1;k<=n;k++)
for(int j=1;j<=n;j++)//用f[i][k] 的值来更新 q[j];
if(j!=k) {
while(l[j]1][0] ][q[j][r[j]-1][1]] - sum[j][q[j][r[j]-1][0]]) r[j]--;
q[j][r[j]][0]=i;q[j][r[j]++][1]=k;
}
}
for(int i=1;i<=n;i++) ans=min(ans,f[m][i]);
printf("%d",ans-cost);
return 0;
} 【Hdu3530】Subsequence
【在线测试提交传送门】
【问题描述】
给定一个包含n个整数序列,求满足条件的最长区间的长度:该区间内的最大数和最小数的差不小于m,且不大于k。
【输入格式】
输入包含多组测试数据:对于每组测试数据: 第一行,包含三个整数n,m和k; 第二行,包含n个整数的序列。
【输出格式】
对于每组测试数据,输出满足条件的最长区间的长度。
【输入样例】
5 0 0 1 1 1 1 1 5 0 3 1 2 3 4 5
【输出样例】
5 4
【数据范围】
1≤n≤100000; 0≤m,k≤100000; 0≤ai≤100000
【解题思路】
用两个单调队列分别维护a[i]前元素中的最大值与最小值的下标,top为最值。 然后当最值之差过大时,a[i]的满足题意的最长字串为最最后操作last与i的距离 其中last取离i最远的一个。
#include1]]<=a[i])tail1--; //top1最大元素
s1[tail1++]=i;
//min
while(top21]]>=a[i])tail2--; //top2最小元素
s2[tail2++]=i;
while(a[s1[top1]]-a[s2[top2]]>k)
{
if(s1[top1]else last2=s2[top2++];
}
if(a[s1[top1]]-a[s2[top2]]>=m)
{
ans=max(ans,i-max(last1,last2));
}
}
cout<return 0;
}
【Hdu3401】Subsequence
【在线测试提交传送门】
【问题描述】
知道之后n天的股票买卖价格(APi,BPi),以及每天股票买卖数量上限(ASi,BSi),问他最多能赚多少钱。开始时有无限本金,要求任两次交易需要间隔W天以上,即第i天交易,第i+W+1天才能再交易。同时他任意时刻最多只能拥有MaxP的股票。
【输入格式】
第一行,一个整数t,表示有t组测试数据,对于每组测试数据: 第一行,包含三个整数T,MaxP和W,(0 ≤ W < T ≤ 2000, 1 ≤ MaxP ≤ 2000) 。 接下来T行,每行四个整数,APi,BPi,ASi,BSi( 1≤BPi≤APi≤1000,1≤ASi,BSi≤MaxP)。
【输出格式】
对于每组测试数据,输出一个整数,表示赚的最多的钱。
【输入样例】
1 5 2 0 2 1 1 1 2 1 1 1 3 2 1 1 4 3 1 1 5 4 1 1
【输出样例】
3
【解题思路】
易写出DP方程 dp[i][j]=max{dp[i-1][j],max{dp[r][k]-APi[i]*(j-k)}(0
#include j)}
struct node
{
int x;//存dp[i-w-1][k]+APi[i]*k或dp[i-w-1][k]+BPi[i]*k
int p;//当前持股数
} q[2005],temp;
int front,back;
int main()
{
int cas;
scanf("%d",&cas);
for(; cas--;)
{
scanf("%d%d%d",&T,&MaxP,&W);
for(int i=1; i<=T; ++i)
scanf("%d%d%d%d",APi+i,BPi+i,ASi+i,BSi+i);
for(int i=0; i<=T; ++i)
for(int j=0; j<=MaxP; ++j)
dp[i][j]=-inf;
for(int i=1; i<=W+1; ++i)
for(int j=0; j<=ASi[i]; ++j)
dp[i][j]=(-APi[i]*j);
for(int i=2; i<=T; ++i)
{
for(int j=0; j<=MaxP; ++j)
dp[i][j]=max(dp[i][j],dp[i-1][j]);
if(i<=W+1) continue;
//买入
front=back=1;
for(int j=0; j<=MaxP; ++j)
{
temp.p=j;
temp.x=dp[i-W-1][j]+APi[i]*j;
for(;front1].xfor(;front//卖出
front=back=1;
for(int j=MaxP; j>=0; --j)
{
temp.p=j;
temp.x=dp[i-W-1][j]+BPi[i]*j;
for(;front1].xfor(;frontj;++front);
dp[i][j]=max(dp[i][j],q[front].x-BPi[i]*j);
}
}
int ans=0;
for(int i=0;i<=MaxP;++i)
ans=max(ans,dp[T][i]);
printf("%d\n",ans);
}
return 0;
}
【Poj1742】Coins
【在线测试提交传送门】
【问题描述】
有n种不同面值的硬币,面值分别为A1,A2,A3...An,对应的数量分别是C1,C2,C3...Cn,求能搭配出多少种不超过m的金额。
【输入格式】
输入包含多组测试数据,对于每组测试数据: 第一行,两个整数,n和m;(1≤n≤100;m≤100000) 第二行,2*n个整数,一次表示A1,A2,A3...An,C1,C2,C3...Cn。(1≤Ai≤100000,1≤Ci≤1000) 输入的最后用0 0表示结束。
【输出格式】
对于每组测试数据,依次输出一个整数。
【输入样例】
3 10 1 2 4 2 1 1 2 5 1 4 2 1 0 0
【输出样例】
8 4
【解题思路】
dp[i][j]= 用前i种硬币能否凑成j 递推关系式: dp[i][j] = (存在k使得dp[i – 1][j – k * A[i]]为真,0 < k < m 且下标合法
#include
using namespace std;
bool dp[100 + 16][100000 + 16]; // dp[i][j] := 用前i种硬币能否凑成j
int A[100 + 16];
int C[100 + 16];
int main(int argc, char *argv[])
{
int n, m;
while(cin >> n >> m && n > 0)
{
memset(dp, 0, sizeof(dp));
for (int i = 0; i < n; ++i)
{
cin >> A[i];
}
for (int i = 0; i < n; ++i)
{
cin >> C[i];
}
dp[0][0] = true;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j <= m; ++j)
{
for (int k = 0; k <= C[i] && k * A[i] <= j; ++k)
{
dp[i + 1][j] |= dp[i][j - k * A[i]];
}
}
}
int answer = count(dp[n] + 1, dp[n] + 1 + m , true); // 总额0不算在答案内
cout << answer << endl;
}
return 0;
}
【Hdu4374】 One hundred layer
【在线测试提交传送门】
【问题描述】
有个游戏叫“是男人就下100层”,规则如下: 1.开始时,你在第一层; 2.每一层被分成M个区间,你只能往一个方向走(左或者右),你也可以跳到下一层的同一个区间,比如你现在第y个区间,你将跳到下一层的第y个区间。(1≤y≤M); 3.你最多朝一个方向移动T个区间; 4.每个区间都有一个分数。最后的得分是你经过的各个区间的分数的总和。 求你可以得到的最大得分。
【输入格式】
输入包含多组测试数据,对于每组测试数据: 第一行,4个整数N, M, X, T(1≤N≤100, 1≤M≤10000, 1≤X, T≤M),其中N表示层数,M表示每层的区间数,开始时你在第X个区间,每层最多朝一个方向移动T个区间。 接下来N行,每行M个整数,依次表示每个区间的分数。 (-500≤score≤500)
【输出格式】
对于每组测试数据输出一行一个整数,表示最大得分。
【输入样例1】
3 3 2 1 7 8 1 4 5 6 1 2 3
【输出样例1】
29
【样例说明】
8+7+4+5+2+3=29
#include 【CodeForces372C】 Watching Fireworks is Fun
【在线测试提交传送门】
【问题描述】
一个城镇有n个区域,从左到右1编号为n,每个区域之间距离1个单位距离。节日中有m个烟火要放,给定放的地点a[i] 、时间t[i] ,如果你当时在区域x,那么你可以获得b[i] - | a[i] - x |的开心值。你每个单位时间可以移动不超过d个单位距离。你的初始位置是任意的(初始时刻为1),求你通过移动能获取到的最大的开心值。
【输入格式】
第一行包含3个整数n, m, d (1≤n≤150000; 1≤m≤300; 1≤d≤n). 接下来m行,每行包含3个整数, a[i] , b[i] , t[i] (1≤a[i] ≤n; 1≤b[i] ≤10^9; 1≤t[i] ≤10^9) 输入保证t[i]≤t[i+1] (1≤i<m)
【输出格式】
一行,一个整数,表示最大开心值。
【输入样例1】
50 3 1 49 1 1 26 1 4 6 1 10
【输出样例1】
-31
【输入样例2】
10 2 1 1 1000 4 9 1000 4
【输出样例2】
1992
【解题思路】
首先设dp[i][j]为到放第i个烟花的时候站在j的位置可以获得的最大开心值。那么我们可以很容易写出转移方程:
dp[ i ] [ j ] =max(dp[ i - 1] [ k ]) + b[ i ] - | a[ i ] - j | ,其中 max(1,j-t*d)≤min(n,j+t*d) 。
不过我们可以发现b[ i ]是固定的,那么我们转化为求所有| a[ i ] - x |的最小值,即dp[ i ] [ j ] 表示到第i个烟花的时候站在j的位置可以获得的最小的累加值,转移方程:
dp[ i ] [ j ] =min(dp[ i - 1] [ k ])+ | a[ i ] - j | ,其中 max(1,j-t*d)≤k≤min(n,j+t*d)。
由于是求一段区间的最小值,我们可以想到用单调队列维护,维护一个单调升的队列。不过这题有一点不同的是对于当前考虑的位置i来说其右端的点也需要考虑是否进入队列,假设当前考虑位置i,所需维护区间长度为l,如果i+l≤n,那么看他是否能丢进队列。
还有一点需要注意,因为n、m都很大,所以直接开二维肯定炸内存,所以要用滚动数组优化下。
#include1].val) tail--;
que[tail].val=dp[now][i]; que[tail++].index=i;
}
for(int i=1;i<=n;i++){
int l,r;
l=i-k;r=i+k;
if(l<=0) l=1;
while(headif(r<=n){
while(head1].val) tail--;
que[tail].val=dp[now][r]; que[tail++].index=r;
}
dp[now^1][i]=que[head].val+abs(a[j]-i);
}
now^=1;
}
ll Min=dp[now][1];
for(int i=2;i<=n;i++)
Min=min(Min,dp[now][i]);
cout<return 0;
}