链接:https://ac.nowcoder.com/acm/contest/1005/B
题目描述
一列火车n节车厢,依次编号为1,2,3,…,n。每节车厢有两种运动方式,进栈与出栈,问n节车厢出栈的可能排列方式有多少种。
输入描述:
一个数,n(n≤60000)n (n \leq 60000)n(n≤60000)
输出描述:
一个数s表示n节车厢出栈的可能排列方式
示例1
输入
3
输出
5
示例2
输入
50
输出
1978261657756160653623774456
思路:
方案一:暴力枚举
对于栈问题,简单来想只有进栈和出栈的操作
所以直观的来看,直接暴力枚举每个节点情况
\(\begin{cases}1.把下一个数进栈\\2.把当前栈顶元素出栈(如果栈非空)\end{cases}\)
利用递归快速实现,时间复杂度 :\(O(2^N)\)
在这个时间复杂度下很容易TLE
方案二:递推优化 \(O(N^2)\)
因为本题只是要求求出有多少种出栈序列并不关心具体方案,于是我们可以使用递推直接进行统计。设\(S_N\) 表示进栈顺序为 \(1,2,3,4...,N\) 时可能的出栈序列总数。
现在假设序列中位置 \(K\) 的地方有一个数 \(a ,a\)前面有\(K−1\)个数要出栈,a后面有\(N−K\)个数要出栈,而出栈的方案总数分别是 $S_{K−1} $ 和 \(S_{N−K}\) 于是这个大问题就转化成了小问题,我们就要求更小的 \(S_i\),于是有递推公式(很好理解):
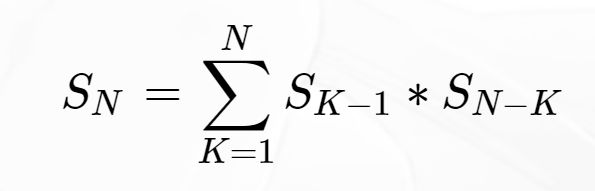
方案三:动态规划 \(O(N^2)\)
动态规划。这里我们要有状态与决策的思想(这个真的很重要,有时与搜索也异曲同工)。我们设 \(F[i,j]\) 是还有 $i \(个元素未入栈,\)j$ 个元素在栈中的方案总数,初始状态是\(F[0,0]=1\),目标状态是\(F[N,0]F\),每一次我们的决策有“让一个数进栈”,“让栈顶的数出栈”,所以方程有:
方案四:数学 \(O(N)\)、
该问题等价于求第 \(N\) 项 \(Ctalan\)数,即 \(C^{N}_{2N} / (N + 1)\)