【PyG进阶学习】一：AGNN算法

一：简介

算法全名：Attention-based Graph Neural Network for Semi-supervised Learning
论文链接：https://arxiv.org/abs/1803.03735

如题目所说，本论文提出的模型是针对于半监督学习领域的一种算法，是一种基于注意力机制的图神经网络。该算法简称为AGNN，在提出AGNN之前，作者介绍了三个算法的大致思路，分别是GNN、GCN、GLN，本文经过个人阅读，作者其大致方向可以概括为：

原本的图神经网络也好，图卷积神经网络也好，本质就是两种网络的组合方式，不断地Stacking，这两种网络分别为聚合层和全连接层，论文称之为 propagation layer和single layer perceptron，翻译过来就是传播层和单层感知机，后文按照聚合层和全连接层的表达习惯进行讲解。简单的说，聚合层就是节点与邻域节点的特征融合，是属于节点级别的处理方式，而全连接层是每个节点单独地将内部特征重新映射到一个新维度的特征向量上，是属于节点内部级别的处理方式。经过作者的实验和分析，图神经网络关键在于聚合层，使其达到了令人瞩目的效果，而这个全连接层并无太大意义，故将这个结构去除，在很大程度上降低了模型的参数量，而本身半监督学习问题大部分都是标注样本不足的，更少的参数量在小规模数据问题上可以更有效地收敛。

下面分别给出GNN、GCN、GLN的简要流程：
1.GNN
首先GNN公式分两步：


H表示第t层的节点的特征矩阵，也可以叫做隐藏层状态，P表示的是一种聚合方式，比如求和，无非用的是矩阵形式。第一个公式表示聚合层，对H进行左乘可以理解为：

每一个节点的聚合方式表现为P矩阵的一个行向量，对所有的节点特征（H）进行加权聚合，每一个节点的加权向量不一样，而且对节点特征聚合时，是逐特征聚合，特征与特征之间不会混合。

第二个公式为全连接层，对H进行右乘，节点之间不会干扰，但是单个节点的特征会混合，而且权重W是共享的，这里作者解释了下，就是说之所以共享相同的权重矩阵W，是因为即可以降低模型复杂度而且保持Graph的不变性（invariance property），此处我用一个例子来具体说一下，对于图中的两个局部区域，假设其图的拓扑结构是类似的，对于聚合层而言，这两个区域的聚合情况也是类似的，所以为了保证这两个局域在算法中具有类似的预测情景，就要保持全连接层的一致，所以采用共享权重的方式对每一个节点加权。
2.GCN
GCN是图卷积神经网络，堆叠了两层，每一层包含一组聚合层和全连接层，如下公式：

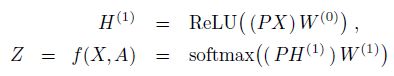
与GNN的区别主要在于矩阵P的构造，详情见GCN论文（以后的文章中我会涉及到这个GCN的具体机制）。
3.GLN
GLN称为Graph Linear Network，关键在于Linear，公式如下：

在GCN基础上，移除非线性部分也就是Relu函数，然后化简到一个公式内。根据作者实验，GLN性能不亚于GNN算法。于是作者在GLN基础上，依然是移除全连接层，并且将聚合层修改为注意力机制。
4.AGNN
上述模型的聚合方式都是静态而且无自适应的方式，就比如说GCN中的聚合方式，其聚合所用矩阵P是通过邻接矩阵和度矩阵构造所得，而其GCN本意是在加法聚合的方式上增加了一个拉普拉斯正则系数，该系数是有一条边上双方节点的邻域大小决定的，这对于固定结构的图而言，是一种固定的聚合逻辑。下面直接给出AGNN公式再分析：

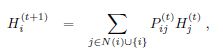
上面给出了四个公式，第一个公式为AGNN第一层，给所有节点的原始特征信息先做一个预处理，乘以一个权重矩阵W0，第二个公式表示了中间层的传播方式，不同于GCN的两层结构，AGNN此处可以设置为L层，而且在中间层不进行全连接过程。第三个公式表示为矩阵P的构造方式，其实矩阵P可以看做是近似于邻接矩阵A的格式，边不存在的地方，元素为0，对于存在边的元素，邻接矩阵中是1，P矩阵的非0元素是一个权重值，这个权重是通过一条边上的两个节点的特征向量的余弦相似度计算后乘以一个自适应系数$\beta$后得到的，每一层聚合层中共用一个$\beta$，最后通过softmax使权重总和为1。最后一个公式在最后一层输出前再进行一次全连接。 矩阵P元素如下：

由此AGNN的训练参数仅仅只有两个权重矩阵W0和W1，以及L个$\beta$。
5.实验结果



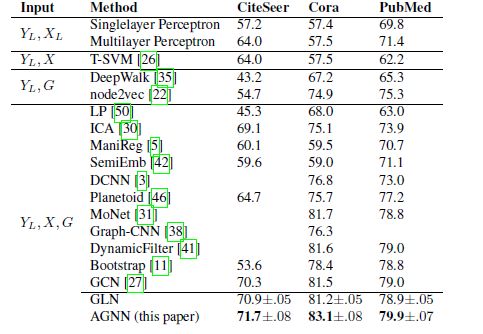
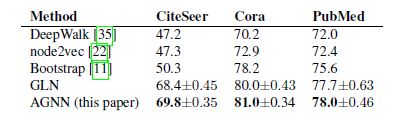
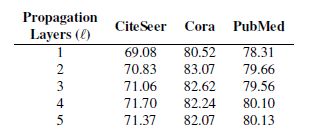
前两个图是在数据预处理方式不同的情况下的效果对比，第三个图是AGNN效果与层数的关系，可以看到层数加深后，效果有一定提高。

二：源码分析

用的是Pytorch-Geometric官方库中实现的代码：

代码链接：https://github.com/rusty1s/pytorch_geometric/blob/master/torch_geometric/nn/conv/agnn_conv.py

1.forward过程

def forward(self, x, edge_index):
    """"""
    edge_index, _ = remove_self_loops(edge_index)
    edge_index, _ = add_self_loops(edge_index,
                                   num_nodes=x.size(self.node_dim))

    x_norm = F.normalize(x, p=2, dim=-1)

    return self.propagate(edge_index, x=x, x_norm=x_norm,
                          num_nodes=x.size(self.node_dim))

首先清理下个别的自环，算是数据清洗吧，然后全部增加自环；计算当前矩阵X特征向量的正则化结果（用于后面求余弦相似度）；调用propagate函数开始信息聚合。
2.message过程

def message(self, edge_index_i, x_j, x_norm_i, x_norm_j, num_nodes):
     # Compute attention coefficients.
     beta = self.beta if self.requires_grad else self._buffers['beta']
     alpha = beta * (x_norm_i * x_norm_j).sum(dim=-1)
     alpha = softmax(alpha, edge_index_i, num_nodes)

     return x_j * alpha.view(-1, 1)

首先定义一个训练参数$\beta$，代码第二行计算余弦相似度并且乘以$\beta$，然后求和（参考AGNN五条公式第四条），最后进行softmax。

三：实际应用

代码链接：https://github.com/rusty1s/pytorch_geometric/blob/master/examples/agnn.py

def __init__(self):
    super(Net, self).__init__()
    self.lin1 = torch.nn.Linear(dataset.num_features, 16)
    self.prop1 = AGNNConv(requires_grad=False)
    self.prop2 = AGNNConv(requires_grad=True)
    self.lin2 = torch.nn.Linear(16, dataset.num_classes)

def forward(self):
    x = F.dropout(data.x, training=self.training)
    x = F.relu(self.lin1(x))
    x = self.prop1(x, data.edge_index)
    x = self.prop2(x, data.edge_index)
    x = F.dropout(x, training=self.training)
    x = self.lin2(x)
    return F.log_softmax(x, dim=1)

首先第一个是全连接层即W0配合Relu，然后两层聚合层即L=2，最后再加一个全连接层W1，通过softmax获得结果。后面训练的时候，损失函数为F.nll_loss，事实上，在Pytorch中，交叉熵CrossEntropyLoss和log_softmax+nll_loss效果是一样的（这个以后再说）。