算法与数据结构-线段树

前言

大四重拾算法与数据结构，所有内容为自己的阶段小结所以并不是技术性文章，如有兴趣阅读，遇到问题不妨给我留个言，万分感谢！
线段树
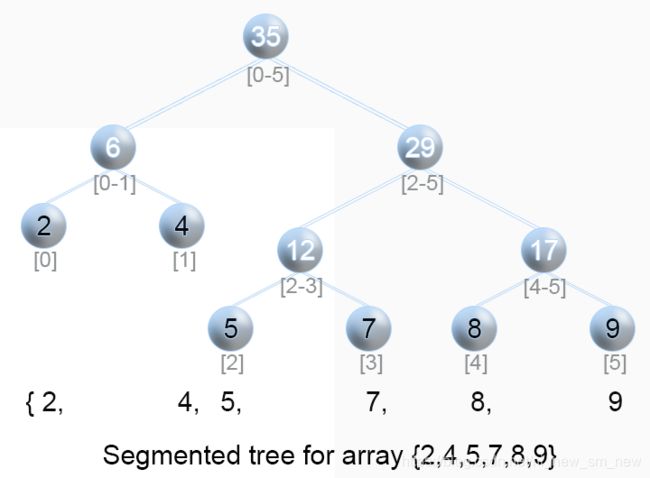
线段树可以看做是一颗完全二叉树(为了方便查找左右结点)
线段树是树中的一种特殊的数据结构，所有的数据结构写出来都是为了更快速的解决某些特殊的问题
线段树的描述与解法在LeetCode的一个题目上描写的很具体，下面给出描述

Segment tree is a very flexible data structure, because it is used to
solve numerous range query problems like finding minimum, maximum,
sum, greatest common divisor, least common denominator in array in
logarithmic time.

具体题目链接: 307. Range Sum Query - Mutable

也就是说每个节点存储的都是一个范围内的具体特征，这个特征可以是某个范围值的和，也可以是这个范围的值的最大值等等
下面附上这种数据结构的代码

package SegmentTree;

//线段树
public class SegmentTree {
	private E[] data;
	private E[] tree;
	private Merger merger;

	public SegmentTree(E[] arr, Merger merger) {
		this.merger = merger;
		data = (E[]) new Object[arr.length];
		for (int i = 0; i < arr.length; i++) {
			data[i] = arr[i];
		}
		// 线段树的大小最大为数组的4倍
		tree = (E[]) new Object[arr.length * 4];
		bulidSegmentTree(0, 0, arr.length - 1);
	}

	// 在treeIndex的位置创建[l...r]的线段树
	private void bulidSegmentTree(int treeIndex, int l, int r) {
		if (l == r) {
			tree[treeIndex] = data[l];
			return;
		}
		int leftTreeIndex = leftChild(treeIndex);
		int rightTreeIndex = rightChild(treeIndex);
		int mid = l + (r - l) / 2;

		bulidSegmentTree(leftTreeIndex, l, mid);
		bulidSegmentTree(rightTreeIndex, mid + 1, r);
		tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
	}

	public int getSize() {
		return data.length;
	}

	public E get(int index) {
		if (index < 0 || data.length <= index)
			return null;
		return data[index];
	}

	private int rightChild(int treeIndex) {
		return treeIndex * 2 + 2;
	}

	private int leftChild(int treeIndex) {
		return treeIndex * 2 + 1;
	}

	// 返回区间 [queryL...queryR]的值
	public E query(int queryL, int queryR) {
		if (queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length || queryL > queryR)
			throw new IllegalArgumentException("Index is illegal.");
		return query(0, 0, data.length - 1, queryL, queryR);
	}

	private E query(int treeIndex, int l, int r, int queryL, int queryR) {
		if (l == queryL && r == queryR) {
			return tree[treeIndex];
		}
		int leftTreeIndex = leftChild(treeIndex);
		int rightTreeIndex = rightChild(treeIndex);
		int mid = l + (r - l) / 2;
		// treeIndex的节点分为[l...mid]和[mid+1...r]两部分
		if (queryL >= mid + 1) {
			// 如果全在左孩子的范围内
			return query(rightTreeIndex, mid + 1, r, queryL, queryR);
		} else if (queryR <= mid)
			// 如果全在右孩子的范围内
			return query(leftTreeIndex, l, mid, queryL, queryR);
		// 如果两个范围都有的话 分成两段递归在相加 也就是左边界在左孩子范围 右边界在右孩子的范围
		// [l...mid] 中找 [queryL...mid]
		// [mid + 1 ... r] 中找[mid + 1 ...queryR]
		E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
		E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
		return merger.merge(leftResult, rightResult);
	}

	public void set(int index,E e) {
		 if(index < 0 || index >= data.length)
	            throw new IllegalArgumentException("Index is illegal");
		 data[index] = e;
		 //更新线段树
		 set(0 ,0 ,data.length -1 ,index ,e);
	}

	// 在以treeIndex为根的线段中更新index的值e
	private void set(int treeIndex, int l, int r, int index, E e) {
		if (l == r) {
			tree[treeIndex] = e;
			return;
		}
		// treeIndex的节点分为[l...mid]和[mid+1...r]两部分
		int leftTreeIndex = leftChild(treeIndex);
		int rightTreeIndex = rightChild(treeIndex);
		int mid = l + (r - l) / 2;
		if (index > mid + 1) {
			set(rightTreeIndex, mid + 1, r, index, e);
		} else {
			set(leftTreeIndex, l, mid, index, e);
		}
		// 更新值后要更新他的父节点的值
		tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
	}

}

Merger是我们设置想要在线段树中每个节点表示的值具体是什么

package SegmentTree;
interface Merger {
	E merge(E a,E b);
}