数据结构与算法分析:(三)单向链表
一、什么是链表?
链表是一种物理上非连续、非顺序的存储结构,数据元素之间的顺序是通过每个元素的指针(类似C语言中的指针,Java中是引用)关联的。
链表由一系列节点组成,每个节点一般至少会包含两部分信息:一部分是元素数据本身,另一部分是指向下一个元素地址的“指针”。这样的存储结构让链表相比其他线性的数据结构来说,操作会复杂一些。
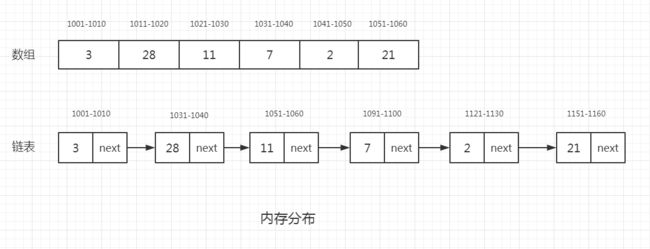
说到链表,我们经常拿来与数组比。我们先看下面一张图再来对比它们的各自的优劣。
从图中我们看到,数组需要一块连续的内存空间来存储,对内存的要求比较高。如果我们申请一个 100MB 大小的数组,当内存中没有连续的、足够大的存储空间时,即便内存的剩余总可用空间大于 100MB,仍然会申请失败。
而链表恰恰相反,它并不需要一块连续的内存空间,它通过“指针”将一组零散的内存块串联起来使用,所以如果我们申请的是 100MB 大小的链表,根本不会有问题。
这里先思考一下下面这个问题。
Q:数组在实现上为什么使用的是连续的内存空间?
- A:可以借助 CPU 的缓存机制,预读数组中的数据,所以访问效率更高。而链表在内存中并不是连续存储,所以对 CPU 缓存不友好,没办法有效预读。
Q:上一答案中CPU缓存机制指的是什么?为什么就数组更好了?
- A: CPU在从内存读取数据的时候,会先把读取到的数据加载到CPU的缓存中。而CPU每次从内存读取数据并不是只读取那个特定要访问的地址,而是读取一个数据块并保存到CPU缓存中,然后下次访问内存数据的时候就会先从CPU缓存开始查找,如果找到就不需要再从内存中取。这样就实现了比内存访问速度更快的机制,也就是CPU缓存存在的意义:为了弥补内存访问速度过慢与CPU执行速度快之间的差异而引入。
- A: 对于数组来说,存储空间是连续的,所以在加载某个下标的时候可以把以后的几个下标元素也加载到CPU缓存这样执行速度会快于存储空间不连续的链表存储。
二、链表的分类
- 单向链表
- 双向链表
- 循环链表
- 松散链表
下面我重点分析一下单向链表的一些主要操作。
1、单向链表
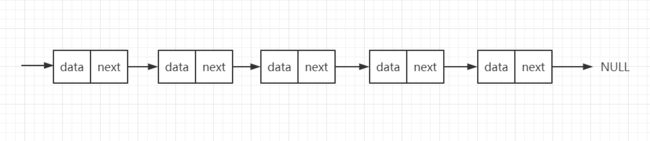
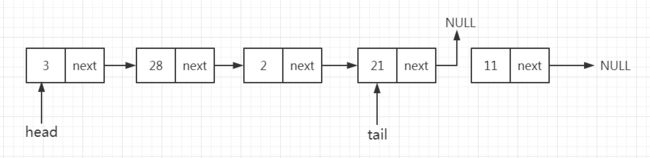
我们刚刚讲到,链表通过“指针”将一组零散的内存块串联在一起。其中,我们把内存块称为链表的“结点”。为了将所有的结点串起来,每个链表的结点除了存储数据之外,还需要记录链上的下一个结点的地址。如下图所示,我们把这个记录下个结点地址的指针叫作后继指针 next。
从我画的单链表图中,你应该可以发现,其中有两个结点是比较特殊的,它们分别是第一个结点和最后一个结点。我们习惯性地把第一个结点叫作头结点,把最后一个结点叫作尾结点。其中,头结点用来记录链表的基地址。有了它,我们就可以遍历得到整条链表。而尾结点特殊的地方是:指针不是指向下一个结点,而是指向一个空地址 NULL,表示这是链表上最后一个结点。
(1)、申请一个链表
public class ListNode {
public int data;
public ListNode next;
public ListNode(int data) {
this.data = data;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public void setNext(ListNode next) {
this.next = next;
}
public ListNode getNext() {
return this.next;
}
}
链表的主要操作
- 遍历链表
- 插入一个元素:插入一个元素到链表中
- 删除一个元素:移除并返回链表中指定位置的元素
链表的辅助操作
- 删除链表:移除链表中的所有元素(清空链表)
- 计数:返回链表中元素的个数
- 查找:寻找从链表表尾开始的第n个节点(node)
(2)、链表的遍历
假设表头指针指向链表中的第一个结点。遍历链表需要完成以下几个步骤:
- 沿指针遍历
- 遍历时显示节点的内容
- 当next指针的值为NULL时,结束遍历
通过遍历链表来对链表元素进行计数:
/**
* 统计链表节点的个数
* @param head 链表头结点
* @return
*/
public int LinkedListLength(ListNode head) {
int len = 0;
ListNode cur = head;
while (cur != null) {
len++;
cur = cur.getNext();
}
return len;
}
时间复杂度为O(n),用于扫描长度为n的链表。
空间复杂度为O(1),仅用于创建临时变量。
(3)、单向链表的插入
单向链表的插入可以分为以下3种情况
- 在链表的头前插入一个新结点(链表的开始出)
- 在链表的尾后插入一个新结点(链表的结尾出)
- 在链表的中间插入一个新结点(随机位置)
a、在单向链表的开头插入结点
若需要在表头节点前插入一个新结点,只需要修改一个next指针,可通过如下两步完成:
如果需要在表尾部插入新结点,则需要修改两个next指针。
- 新结点的next指针指向NULL
- 最后一个结点的指针指向新结点
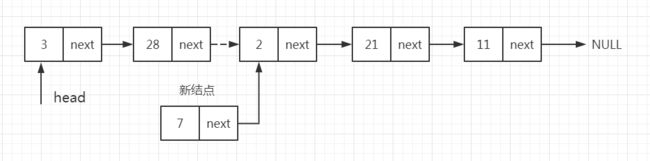
假设给定插入新结点的位置,在这种情况下,需要修改两个next指针:
- 如果位置3增加一个元素,则需要将指针定位于链表的位置2,。即需要从表头开始经过两个结点,然后插入新结点。假设第二个结点为位置结点,新结点的next指针指向位置结点(我们要在此处增加新结点)的下一个结点
- 位置结点的next指针指向新结点
/**
* 单向链表List节点进行插入操作
* @param head 链表头结点
* @param insertNode 插入结点
* @param position 插入位置
* @return
*/
public ListNode insertInLinkedList(ListNode head, ListNode insertNode, int position) {
// 如果链表为空,则插入的节点即为头结点
if (head == null) return insertNode;
// 获取该链表的结点数
int size = linkedListLength(head);
if (position < 1 || position > size + 1) {
System.out.println("Position of node to insert is invalid.The valid input are 1 to "
+ (size + 1));
return head;
}
// 否则,插入元素要么是在头插入,要么是在尾节点,或是中间
if (position == 1) {
insertNode.setNext(head);
return insertNode;
} else {
// 在链表的中间或尾部插入
ListNode prev = head;
int count = 1;
while (count < position - 1) {
prev = prev.getNext();
count++;
}
ListNode cur = prev.getNext();
insertNode.setNext(cur);
prev.setNext(insertNode);
}
return head;
}
时间复杂度为O(n)。在最坏情况下,可能需要在链表尾部插入结点。
空间复杂度为O(1)。仅用于创建一个临时变量。
(4)、单向链表的删除
单向链表的删除操作,也分为三种情况:
- 删除链表的表头(第一个)结点
- 删除链表的表尾(最后一个)节点
- 删除链表的中间的节点
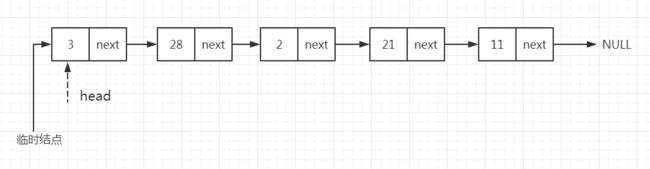
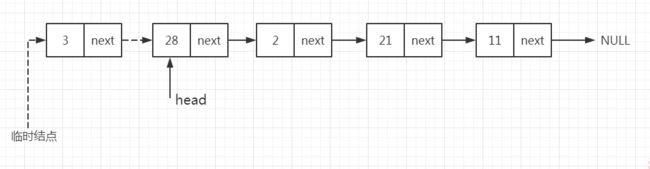
a、删除单向链表表头结点
删除链表的第一个结点,可以通过两步实现:
- 创建一个临时结点,它指向表头指针所指的结点。
- 修改表头指针的值,使其指向下一个结点,并移除临时结点。
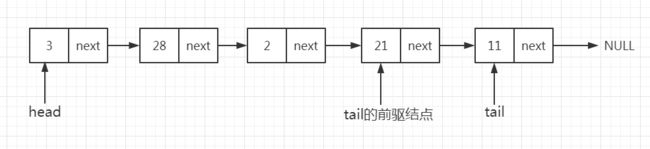
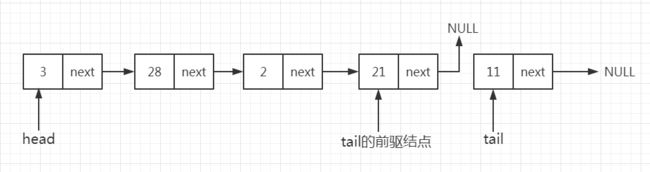
b、删除单向链表的最后一个结点
这种情况下,操作比删除第一个结点要麻烦一点,因为算法需要找到表尾节点的前驱节点。这需要三步来实现:
- 遍历链表,在遍历时还要保存前驱(前一次经过)结点的地址。当遍历到链表的表尾时,将有两个指针,分别是表尾结点的指针tail(表尾)即指向表尾结点的前驱结点的指针。
- 将表尾的前驱节点的next指针更新为NULL。
- 移除表尾节点。
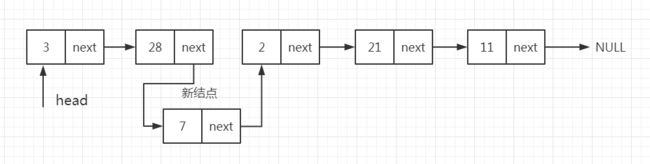
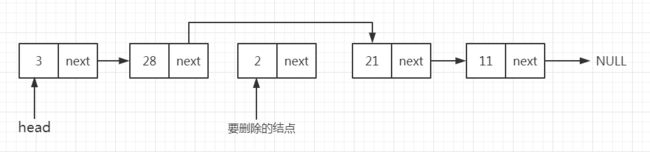
c、删除单向链表中间一个结点
在这种情况下,删除的结点总是位于两个结点之间,因此不需要更新表头和表尾的指针。该删除操作通过两步实现:
- 在遍历时保存前驱(前一次经过的)结点的地址。一旦找到被删除的结点,将前驱结点next指针的值更新为被删除结点的next指针的值。
- 移除需要删除的当前结点。
d、单向链表删除的代码实现
/**
* 单向链表List的删除操作
* @param head 链表头结点
* @param position 删除位置
* @return
*/
public ListNode deleteNodeFromLinkedList(ListNode head, int position) {
int size = linkedListLength(head);
if (position < 1 || position > size) {
System.out.println("Postition of node to delete is invalid.The valid inputs are 1 to "
+ size);
return head;
}
if (position == 1) {
ListNode cur = head.getNext();
head = null;
return cur;
} else {
ListNode prev = head;
int count = 1;
while (count < position) {
prev = prev.getNext();
count++;
}
ListNode cur = prev.getNext();
prev.setNext(cur.getNext());
cur = null;
}
return head;
}
时间复杂度为O(n)。在最差情况下,可能需要删除链表的表尾节点。
空间复杂度为O(1)。仅用于创建一个临时变量
(5)、删除单向链表
该操作通过将当前结点存储在临时变量中,然后释放当前结点(空间)的方式来完成。当时放完当前结点(空间)后,移动到下一个结点并将其存储在临时变量中,然后不断重复该过程直至释放所有结点。
代码实现:
/**
* 删除单向链表
* @param head 链表头结点
*/
public void deleteLinkedList(ListNode head) {
ListNode tempNode, iterator = head;
while (iterator != null) {
tempNode = iterator.getNext();
iterator = null;
iterator = tempNode;
}
}
时间复杂度为O(n),扫描大小为n的整个建链表。
空间复杂度为O(1):用于创建临时变量。
三、链表、数组的优缺点对比
链表、数组与动态数组的时间复杂度对比: