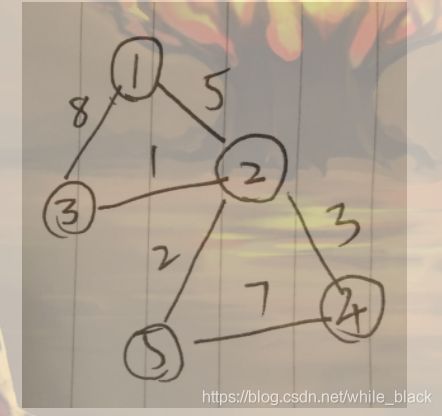
Dijistra算法 和 Dijistra的进阶堆优化的设计（优先队列实现） (单源最短路径，从一个点到其他点的最短距离)

https://www.cnblogs.com/jason2003/p/7222182.html

（1）for先设定从1到2，3的连线值为无穷大，再选择其中到1距离最小节点为新的起点，后从新起点链接到的点继续第一步。

（2）进阶：堆优化。使用从小到大的优先队列，每次选择长度最小的边指向的未选中的节点。

（3）有负权值使用SPFA算法，无负权值用堆优化的Dijistra算法。

for(int i=0;i     {                     //就是需要n-1次的寻找最小权值，就是需要选择剩下的所有节点
        int minn=INF,u;
        
        for(int j=0;j         {                   //因为不知道有从它出来有多少条边，因此全都遍历一遍，
            if(book[j]==0 && dis[j]             {//而且设定就是为dis[]就是起点所有节点的距离，就算没有权值也可以说是无穷大
                minn=dis[j];
                u=j;
            }
        }
        book[u]=1;
        
        for(int j=0;j         {                   //不知道新选择的边有多少条路出去，所以最好全部更新一遍
            if(book[j]==0 && dis[u]+mp[u][j]             {
                dis[j]=dis[u]+mp[u][j];
            }
        }

#include
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
int mp[1010][1010],dis[1010],book[1010],n,m;

void dijkstra(int v0)
{
	for(int i=1;i<=n;i++)//遍历所有的点，得出从起点的各个边
	{
		dis[i]=mp[v0][i];
	}
	book[v0]=1;

	for(int i=0;i>n>>m)
	{
	    memset(dis,INF,sizeof(dis));//把dis数组附最大值（88不是十进制的88，其实很大）
	    memset(book,0,sizeof(book));
	    memset(mp,INF,sizeof(mp));
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(i==j) mp[i][j]=0;
				else mp[i][j]=INF;
			}
		}
		int a,b,c;
		for(int i=0;i>a>>b>>c;
			if(c>first>>second;
		//first--;
		//second--;
		dijkstra(first);

		//if(dis[second]==INF) cout<<"-1"<
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
int mp[1010][1010],dis[1010],book[1010],n,m;

void dijkstra(int v0)
{
	for(int i=1;i<=n;i++)//遍历所有的点，得出从起点的各个边
	{
		dis[i]=mp[v0][i];
	}
	book[v0]=1;

	for(int i=0;i>n>>m)
	{
	    memset(dis,INF,sizeof(dis));//把dis数组附最大值（88不是十进制的88，其实很大）
	    memset(book,0,sizeof(book));
	    memset(mp,INF,sizeof(mp));
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(i==j) mp[i][j]=0;
				else mp[i][j]=INF;
			}
		}
		int a,b,c;
		for(int i=0;i>a>>b>>c;
			if(c>first>>second;
		//first--;
		//second--;
		dijkstra(first);

		if(dis[second]==INF) 
        cout<<"-1"<

 

堆优化：使用优先队列进行堆优化，排列出最小的路径，每次选择出最小的路径进行下一次的运算。

#include 
using namespace std;
int n,m;
struct node{
    int to;
    int w;
};
int edgeNum[100];
vector vec[100];
int dis[100];
bool vis[100];

void addEdge(int a,int b,int w){
    edgeNum[a]++;
    node *p=new node();
    p->to=b;
    p->w=w;
    vec[a].push_back(*p); 
}

void init(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int a,b,w;
        cin>>a>>b>>w;
        addEdge(a,b,w);
        addEdge(b,a,w);
    }
}

void dijkstra(int start){
    memset(dis,0x3f,sizeof(dis));
    dis[start]=0;
    for(int i=0;idis[min_i]+w){
                dis[b]=dis[min_i]+w;
            } 
        } 
        
    }    
}



//dijkstra的堆优化
struct qnode{
    int i_i;
    int dis_i;
    qnode(int i,int dis_i){
        this->i_i=i;
        this->dis_i=dis_i;
    }
}; 
struct myCmp{//从小到大的排序
    bool operator ()(const qnode &p1,const qnode &p2){
        return p1.dis_i > p2.dis_i;
    }
};
priority_queue,myCmp> q;

void dijkstra_2(int start)
{
    memset(dis,0x3f,sizeof(dis));//和SPFA一样，这里最开始全都是无穷大 
    dis[start]=0;
    q.push( qnode(start,dis[start]) );
    while(!q.empty()){
            
        qnode p=q.top();
        q.pop();
    
        int min_i= p.i_i;
        int minV=p.dis_i;
        
        if(vis[min_i]) continue;
        vis[min_i]=true;
        
        for(int i=0; i < edgeNum[min_i] ;i++){
            int b=vec[min_i][i].to;
            int w=vec[min_i][i].w;
            
            if(!vis[b]&&dis[b]>dis[min_i]+w){
                dis[b]=dis[min_i]+w;
                q.push(qnode(b,dis[b]));
            }
        }
        
    }
} 

void print(){
    for(int i=1;i<=n;i++)
        cout<

#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define in(a) a=read()
#define REP(i,k,n) for(long long i=k;i<=n;i++)

#define MAXN 10010
using namespace std;

typedef pair P;

inline long long read()
{
    long long x=0,t=1,c;
    while(!isdigit(c=getchar()))
        if(c=='-')
            t=-1;
    while(isdigit(c))
        x=x*10+c-'0',c=getchar();
    return x*t;
}

long long n,m,s;
long long total=0, head[MAXN], nxt[MAXN<<10], to[MAXN<<10], val[MAXN<<10];
long long dis[MAXN],vis[MAXN];

priority_queue ,greater
 > Q;//优先队列优化，从小到大

inline void adl(long long a,long long b,long long c)
{
    total++;
    to[total]=b;
    val[total]=c;

    nxt[total]=head[a];

    head[a]=total;
    
    return ;
}

inline void Dijkstra()
{
    REP(i,1,n)  dis[i]=2147483647;

    dis[s]=0;

    Q.push( P(0,s) );
    while(!Q.empty())
    {
        long long u=Q.top().second;//取出dis最小的点
        Q.pop();//弹出
        if(vis[u])
            continue;
        vis[u]=1;
        
        for(long long e=head[u]; e; e=nxt[e])
        {
            if(dis[ to[e] ]>dis[u]+val[e])
            {
                dis[to[e]]=dis[u]+val[e];

                Q.push( P( dis[to[e]],to[e] ) );//插入
            }
        }

    }
    return ;
}
/*
5 5 1
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3
0 -3 -1 2 4
*/
int main()
{
    in(n),in(m),in(s); //s指起点
    long long a,b,c;
    REP(i,1,m)  in(a),in(b),in(c),adl(a,b,c);

    Dijkstra();
    REP(i,1,n)  printf("%lld ",dis[i]);
}