Codeforces Round #656 (Div. 3)G. Columns Swaps（补题）

题意：

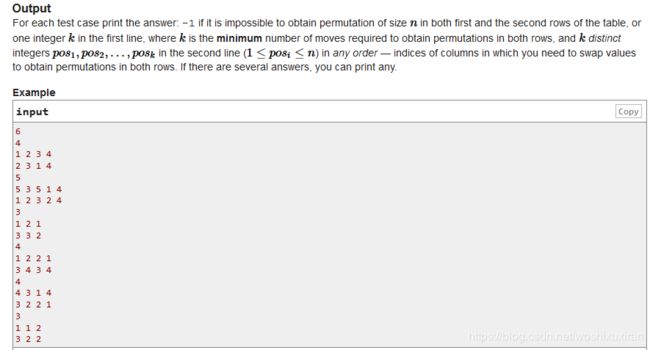
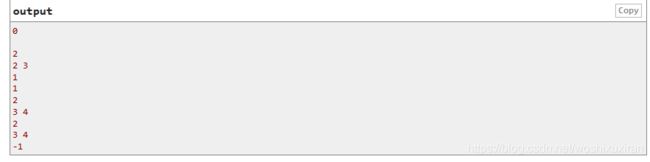
给你两行数（2行n列），交换一些列，让每行都正好有1-n这n个数。问是否可以，可以则输出至少移动多少次，否则输出-1

分析：其实就是一个二分图染色，不会，等题解，到时候再补。（其实代码不少，但是看不懂）

自己用并查集写了一个类似的操作，ac了

将每列的数字当作一个点，如果两列数字在同行，说明一个列要换一个不要。不在同行就说明都要换或者都不要。

因此这就意味着可以用种类并查集去做。

确定同类和异类（最后会有很多类）。重点是有“针对类”，然后选一个去翻转即可。

代码：

    #include
    using namespace std;
    const int N=200005;
    int jud[2*N],pos1[2*N],pos2[2*N],par[2*N],res[2*N],n,ans,tmp;
    bool ji[2*N];
    
    //并查集模板 
    void init(int n)
	{
    	for (int i=1;i<=n;i++) 
			par[i]=i;
    } 
    int find (int x)
    {
     	if (par[x]==x) return x;
    	else return par[x]=find(par[x]);
    } 
    void unite(int x,int y)
    {
      	x=find(x);y=find(y);
      	if (x==y)return;
      	par[x]=y;
    } 
    
    void jjwt()
    {    	
    	scanf("%d",&n);
    	
    	//初始化 
    	for (int i=0;i<=2*n;i++)
    	{
    		pos1[i]=0;pos2[i]=0;res[i]=0;ji[i]=0;jud[i]=0;
		}
    	ans=0;init(2*n);
    	//第一行的输入 
    	for (int i=1;i<=n;i++)
    	{    		
    		scanf("%d",&tmp);
    		jud[tmp]++;
    		if (pos1[tmp]==0)
    			pos1[tmp]=1,pos2[tmp]=i;
    		//相同只可能同一行，同行则异 
    		else if (pos1[tmp]==1)
    			unite(pos2[tmp],i+n),unite(pos2[tmp]+n,i);
    	} 
    	//第二行输入 
    	for (int i=1;i<=n;i++)
    	{
    		scanf("%d",&tmp);
    		jud[tmp]++;
    		if (pos1[tmp]==0)
    			pos1[tmp]=2,pos2[tmp]=i;
    		else if (pos1[tmp]>0)
    		{
    			//同行则异
    			if (pos1[tmp]==2)
    				unite(pos2[tmp],i+n),unite(pos2[tmp]+n,i);
    			else if (pos1[tmp]==1)
    			{
    				if (pos2[tmp]!=i)
    					unite(pos2[tmp],i),unite(pos2[tmp]+n,i+n);
    				//特判两数在同一列，无效数据，下面都不处理 
    				else
    					par[i]=-1,par[i+n]=-1;
    			}	
    			pos1[tmp]=-1;//再遇到就不会进入，免得引起未知异常 
    		}
    	} 
 		//如果不满足两个数，直接扔出去 
    	for (int i=1;i<=n;i++)
    	{
    		if (jud[i]!=2)
    			ans=-1;
		}
		if (ans==-1)
		{
			printf("-1\n");
			return;
		}
		//并查集认祖归宗 
    	for (int i=1;i<=2*n;i++)
    		if (par[i]!=-1)
	    		par[i]=find(par[i]);
    	// 计算每一个祖宗有多少儿子 
    	for (int i=1;i<=n;i++)
    		if (par[i]!=-1)
    			res[par[i]]++;
    	//核心：每一个祖宗有一个对立祖宗（即相异），必须要选一个，自然选小的那一个		
    	for (int i=1;i<=n;i++)
    	{
    		if (par[i]==-1) continue;//注意特判想同的情况 
    		if (res[par[i]]>0&&res[par[i+n]]>=0)
    		{
    			if (res[par[i]]>=res[par[i+n]])//等于很重要，这样不需要调整的就可以不用调整了 
    				res[par[i]]=-1;
				else
					res[par[i+n]]=-1;
			}
			if (res[par[i]]>0)
				ji[i]=1,ans++;
		}
		printf("%d\n",ans);
		for (int i=1;i<=n;i++)//遍历发现可以输出，就记录下来 
			if (ji[i])
				printf("%d ",i);
		printf("\n");
    } 
    int main()
    {
    	int T;
    	scanf("%d",&T);
    	while (T--)
    	{
    		jjwt();
    	}
    	return 0;
    }

这题超级玄学，如果删去pos1[tmp]=-1；一句会莫名其妙的mle，我到现在都不知道怎么mle的。

不过好好想想还是谨慎为好，能少走一次循环就少走一次