自然语言处理——分词算法

引言

分词是自然语言处理中的基本操作，今天我们就来看一下常用的分词算法及实现。

最大匹配算法

所谓的最大匹配指的是匹配最长的单词，通常会指定一个最大长度。根据搜索顺序的不同，主要有前向最大匹配算法、后向最大匹配算法、双向匹配算法。

前向最大匹配算法

所有的分词算法都是基于词典的，假设我们要分词的句子为"我爱北京天安门"，词典如下：

word_dic = ['我','爱','北京天安门','北京','天安门'] #自定义词典

这里假定最大单词长度为5，前向最大匹配算法从句首开始，即尝试从"我爱北京天\安门"中第5个字的位置划一刀，看"我爱北京天"是否在词典内；

然后减小搜索长度，去掉最后面的“门”，看“我爱北京”是否在词典内；

…

最后搜索到“我”这个词在词典内，然后从"我|爱北京天安\门"中抽取“爱北京天安”开始搜索。

代码如下：

# 最大匹配算法

# 前向最大匹配算法
# 利用词典库
max_len = 5 #最大长度
segment = '我爱北京天安门'
seg_list = []
i = 0
while i < len(segment):
    for pos in reversed(range(max_len)):# 最大长度为5，从右边开始减少
        print('judge %s ' %(segment[i:pos+i+1]))
        if segment[i:pos+i+1] in word_dic:
            seg_list.append(segment[i:pos+i+1])
            i = pos+i
            break
    i = i + 1
    
print("/".join(seg_list))

输出如下:

judge 我爱北京天 
judge 我爱北京 
judge 我爱北 
judge 我爱 
judge 我 
judge 爱北京天安 
judge 爱北京天 
judge 爱北京 
judge 爱北 
judge 爱 
judge 北京天安门 
我/爱/北京天安门

最后输出的“我/爱/北京天安门”就是分词结果。

因为是基于最大匹配，因此这个算法能将“北京天安门”正确的划分成一个词。

后向最大匹配算法

后向最大匹配算法顾名思义，就是从句尾开始，这里最大长度也是5，即看句子“我爱\北京天安门”中的“北京天安门”是否在词典内，这里显然在；
然后看“我爱”是否在词典内，不在词典内；
然后去掉最前面的“我”，看“爱”是否在词典内，在；
然后看“我”是否在词典内，在。

代码如下：

# 后向最大匹配算法
max_len = 5 #最大长度
segment = '我爱北京天安门'
seg_list = []
i = len(segment)
while i > 0:
    for pos in reversed(range(max_len)):
        if i >= pos + 1:
            print('judge %s ' %(segment[i-pos-1:i]))
            if segment[i-pos-1:i] in word_dic:
                seg_list.append(segment[i-pos-1:i])
                i = i - pos
                break
    i = i -1
    
print("/".join(reversed(seg_list)))

输出:

judge 北京天安门 
judge 我爱 
judge 爱 
judge 我 
我/爱/北京天安门

最后得到的结果也是:“我/爱/北京天安门”。

这里两个算法的分词结果是一样的，因为我们的句子简单。其实存在10%的情况下结果不一样，也就产生了双向匹配算法。

双向匹配算法

双向最大匹配算法的原理就是将正向最大匹配算法和后向最大匹配算法进行比较，然后根据大颗粒度词越多越好，非词典词和单字词越少越好的原则，选取其中一种分词结果输出。

具体如下：

• 如果分词数量结果不同，那么取分词数量较少的那个
• 如果分词数量结果相同：
  • 分词结果相同，可以返回任何一个
  • 分词结果不同，返回单字数比较少的那个
  • 如果单字数个数也相同，则任意返回一个

这里就不写代码实现了。

最大匹配算法的缺点是什么呢？

• 只能得到局部最优
• 效率低
• 没有考虑语义

为了说明考虑语义这一点，我们换一个句子“我们经常有意见分歧”，词典如下：

word_dic = ['我们','有','经常','有意见','意见','分歧'] #自定义词典

分词的结果为:

“我们/经常/有意见/分歧”，因为是基于最大匹配的，导致“有意见”被分成一个词，如果考虑语义的话，这里应该是：“我们/经常/有/意见/分歧”，这句话说的是意见分歧，而不是有意见。

下面我们看如何考虑语义(这里实际上是考虑词语“有意见”和“意见”出现的概率大小，实际上要考虑语义的话，还要考虑句子的上下文)。

N-Gram模型

N-Gram模型属于语言模型(Language Model)的一种，语言模型估计用于估计不同词语出现的相关概率。

对于语言序列$w_1,w_2,\cdots ,w_n$，语言模型计算该序列出现的概率，即计算$P(W)=P(w_1,w_2,\cdots ,w_n)$，语言模型就是对语句的概率分布建模。

比如可以通过序列中的前几个词来计算出现下一个词的概率。
$P(w_5|w_1,w_2,w_3,w_4)$。

我们知道，计算事件$B$发生的条件下事件$A$发生的条件概率为：
$$P(A|B)=\frac{P(A,B)}{P(B)}$$

基于链式法则，我们可以把这个公式写成下面的样子：
$$P(w_1,w_2,\cdots ,w_n)=P(w_1)P(w_2|w_1)\cdots p(w_n|w_1,\cdots ,w_{n-1})\text{\hspace{1em}(1)}$$

通俗的说法就是出现单词$w_1$，然后出现$w_2$的概率，乘以出现单词$w_1,w_2$条件下出现$w_3$的概率…

在统计语言模型中，我们可以采用极大似然估计来计算每个词出现的条件概率，即

$$P(w_i|w_1,\cdots ,w_{i-1})=\frac{C(w_1,w_2,\cdots ,w_i)}{C(w_1,w_2,\cdots ,w_{i-1})}\text{\hspace{1em}(2)}$$

其中$C(\cdot )$表示子序列在训练集中出现的次数，就是频次。

对于任意长的语句，根据极大似然估计直接计算$P(w_i|w_1,w_2,\cdots ,w_{i-1})$显然不现实。
比如计算
$$\begin{gathered} P(你有没有搞错)=P(你)\cdot P(有|你)\cdot P(没|你有) \\ P(有|你有没)\cdot P(搞|你有没有)\cdot P(错|你有没有搞) \end{gathered}$$

因为语言是创造性的，你可能会碰到“一给我里giaogiao，你有没有搞错。”，这种序列可能你的训练集中根本就没有(最近流行的网络词+随意组合)，导致这个序列的概率是零。

为了解决这个问题，我们引入了马尔科夫假设(Markov assumption)，也就是假设当前词出现的概率只依赖于前$n-1$个词，比如，如果$n=2$:
$$P(错|你有没有搞)\approx P(错|搞)$$
或者如果$n=3$：
$$P(错|你有没有搞)\approx P(错|有搞)$$

我们可知，马尔科夫假设的一般等式为：
$$P(w_i|w_1{w}_2\cdots w_{i-1})\approx P(w_i|w_{i-(n-1)}\cdots w_{i-1})\text{\hspace{1em}(3)}$$

有了上面的知识，就可以引出本节的主题了。
基于马尔科夫假设，即假设当前词出现的概率只依赖于前$n-1$个词，我们能定义N-Gram模型如下：

$$P(w_i|w_1{w}_2\cdots w_{i-1})\approx P(w_i|w_{i-(n-1)}\cdots w_{i-1})\text{\hspace{1em}(4)}$$

其中最简单的情况是$n=1$时的Unigram模型，和$n=2$时的Bigram模型。

$n=1$ (Unigram,假设每个单词都是独立的)：
$$P(w_1{w}_2\cdots w_n)\approx \prod _{i}P(w_i)\text{\hspace{1em}(5)}$$

$n=2$ (Bigram，只依赖前面一个词)：
$$P(w_1{w}_2\cdots w_n)\approx P(w_i|w_{i-1})\text{\hspace{1em}(6)}$$

我们以一个例子来理解Bigram模型和公式$(2)$，为了考虑到句首词和句尾词，我们引入了句首符号和句尾符号。

假设一个简单的语料库中有下面三个句子：

 I am Sam 
 Sam I am 
 I do not like green eggs and ham 

可以计算下面这些bigram的概率：
P(I|) = 2/3 = 0.67 ，以I开头的句子有$2$个，总共有$3$个句子，因此概率为$\frac{2}{3}$(Markdown语法不好打<>符号，因此用代码的形式。)
P(Sam|)=1/3 = 0.33
P(am|I)=2/3 = 0.67,I出现了$3$次，I am出现了$2$次。
P(|Sam)=1/2=0.5,Sam出现了$2$次，Sam作为句尾的句子有$1$个（出现了$1$次）。
P(Sam|am)=1/2=0.5
P(do|I)=1/3=0.33

接下来看一下如何基于unigram模型来考虑分词的语义。因为unigram是最简单的，这里的重点是介绍分词，而不是N-Gram，后面会有文章重点介绍N-Gram。

unigram就是把每个词语都当成是独立的，所以我们需要一个分好词的句子，这里可以通过人工分词或流行的工具。

import jieba

print(jieba.lcut('我们经常有意见分歧,你对我是不是有意见啊，你有什么意见你就直说'))

尝试用结巴分词，无法得到’有意见’这个词语，干脆自定义一个了。

words= ['我们','经常','有','意见','分歧','她','说','你','对','我','是不是','有意见','啊','你','有','什么','意见','就','直说'] 

假设上面的words是人工分词的一个结果。

定义n_grams函数如下：

def n_grams(words,n=1):
    ngrams = []
    for i in range(len(words)-n+1):
        seq = words[i:i+n]
        ngrams.append(' '.join(seq))
    return ngrams

这里直接将词典传入即可：

unigram = n_grams(words)
print(unigram)

因为是概率模型，我们要计算每个词语出现的次数，所以可以通过下面的代码来实现：

from collections import Counter
c = Counter(unigram)
print (dict(c))

这样就可以知道每个词语出现的次数了，除以词语的总数就是相应的概率。

现在假设我们得到了两种划分：“我们/经常/有/意见/分歧”和“我们/经常/有意见/分歧”。

利用unigram模型来计算每种划分的概率，比如计算P(我们/经常/有/意见/分歧)=P(我们)P(经常)P(有)P(意见)P(分歧)。

这里由于是概率的连乘，可能出现向下溢出的情况，因此我们对整个式子取对数(还要乘以-1)，变成了相加。最后还是比较结果的大小即可。我们要选择小的值。

>>> import math
>>> math.log(0.9)
-0.10536051565782628
>>> math.log(0.1)
-2.3025850929940455

本来是要求概率连乘最大的，乘以-1后，变成求对数值之和最小的。

words_size = len(words)
def compute_result(c,word_list):
    result = 0
    for w in word_list:
        result = result - math.log(c[w]/words_size)
    return result

这样我们就可以来评估选用哪个句子好了：

import math
s1 = compute_result(c,'我们/经常/有/意见/分歧'.split('/')) #句子1的概率
s2 = compute_result(c,'我们/经常/有意见/分歧'.split('/')) #句子2的概率
    
print('s1=%s, s2=%s ,s1 > s2 = %s' %(s1,s2,s1 > s2))

这里打脸了啊，本来是要解释为什么选择“有/意见”而不是“有意见”，结果不太理想，我们来分析下原因：

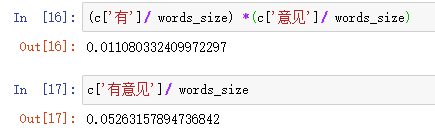
由于把“有/意见”变成两个词语后，它们概率之积反而小于“有意见”的概率的。这说明我们的语料库是不够丰富的。

好了，我们来看下这种方法的缺点。如果有很多种可能的分词组合，我们需要把每种分词组合的结果都计算出来，然后从中选一个概率之积最大的。如果要分词的序列很长，那么就会非常耗时，下面介绍一种动态规划的方法来解决这个问题。

维特比算法

以“我们经常有意见分歧”这句话为例，来解释下维特比算法的主要思想。还是以上面那个不太丰富的词典作为我们的分词词典。
这里给未知词设定一个概率，防止出现未知词概率为零的情况。

从上面我们可以简单的计算出概率和对应的-log(x)。

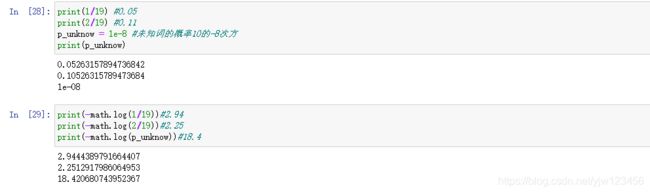
我们先画一个下面这样的图：

上图中的每个连线代表一个词语，然后我们把每个词语的-log(x)值在线上标出来。

比如“我”在词典中是有出现的，而“们”没有出现，其中“有”出现了2次，因此它的值要小一点。

上面是一个字作为词语出现的概率，下面我们画两个字作为词语出现的连线，并且写出对应的-log(x)。

从“我”左边的圆圈连接到“们”右边的圆圈，代表“我们”这个词语出现过。同理还有“经常”、“意见”和“分歧”。

接着，我们画三个字作为词语出现的连线，并写出对应的-log(x)。

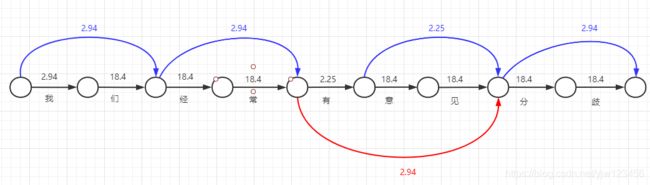
在我们这个简单的词典里面，三个字的词语只有“有意见”，因此连了一根线。
由于词典里面没有三个字以上的词语，因此我们最终的连线结果就如此了。

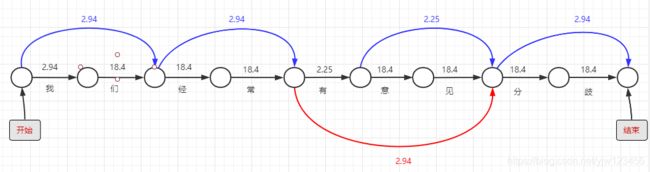
我们为句首增加个开始，句尾增加个结束。上图可以看成是由开始到结束的路径图，有多种连线就有多条路径，每一条路径都对应一种分词结果，我们要找到经过连线上数值之和最小的一条路径。

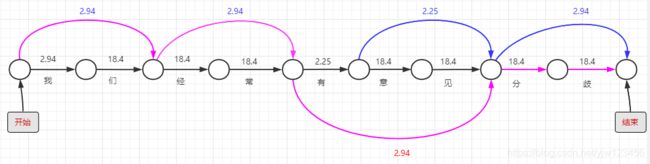
以上图粉色连线路径为例，得出的分词结果是：“我们/经常/有意见/分/歧”。

那么如何找到连线数值之和最小的一条路径呢。

我们把上图每个节点标个号，以方便描述。

假设dp(10)表示从节点1到节点10的最短路径的值，那么
dp(9)就表示从节点1到节点9的最短路径的值
…
dp(2)表示从节点1到节点2的最短路径的值。

我们先自顶向下的考虑问题，假设要计算dp(10)的值，我们有两种方法：dp(8)+2.94和dp(9)+18.4。其实这是一个递归调用，我们可以画出递归调用树：

详情见动态规划

上面简单的画了一下，从上图可以看出，有重叠子问题：dp(8)。如果我们画出完整的树，就可以看到很多重叠子问题，那么可以通过记忆化搜索的方式来优化。这里就不展开了，直接介绍动态规划的方法是如何求解的。

动态规划采用自底向上的思想，从dp(1)的值开始计算，这里可定义dp(1)=0。

那么dp(2)=dp(1) + 2.94，因为节点1到节点2只有一条路径，所以也是最短路径(值最小的路径)。

dp(3)=dp(2) + 18.4 = 21.34，这只是其中一条路径，还有一条路径计算直接是节点1到节点3：2.94。所以dp(3)取其中最小者：2.94。

下面用代码来实现这个过程。

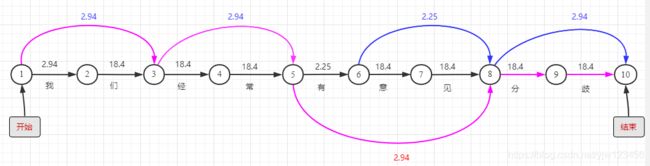
首先我们用有向无环图结构来构建出上面这个图。用python中的字典来描述，key是当前节点，value也是一个字典。value字典里面的key是指向当前节点的节点，值是-log(x)的值与对应的词语组成的元组。

graph = {
        1: {1: (1, '')},
        2: {1: (2.94, '我')},
        3: {2: (18.4, '们'), 1: (2.94, '我们')},
        4: {3: (18.4, '经')},
        5: {4: (18.4, '常'),3: (2.94, '经常')},
        6: {5: (2.24, '有')},
        7: {6: (18.4, '意')},
        8: {7: (18.4, '见'), 6: (2.25, '意见'), 5: (2.94, '有意见')},
        9: {8: (18.4, '分')},
        10: {9: (18.4, '歧'), 8: (2.94, '分歧')}
    }

下面就是核心代码了：

dp = {1:0}
path = {1:0}
for i in range(2,11):#从2到10
    best_dist = float('inf')
    for v,d in graph[i].items():
        if d[0] + dp[v] < best_dist:
            best_dist = d[0] + dp[v] #最短的距离
            path[i] = v #到i最短的顶点是v
            dp[i] = best_dist#记录报端的距离

segments = []
pre = 10#最后一个节点是10
while pre != 1:
    v= path[pre]
    segments.insert(0,graph[pre][v][1])#逆序插入到列表中
    pre = v

print("/".join(segments))

path中记录的是到当前顶点距离最短的顶点，再结合graph就可以遍历出来最终结果。

这就是维特比算法的简单实现。

参考

1. https://www.cnblogs.com/xuelisheng/p/9712973.html
2. https://blog.csdn.net/weixin_44735126/article/details/100941826
3. https://towardsdatascience.com/learning-nlp-language-models-with-real-data-cdff04c51c25
4. https://web.stanford.edu/~jurafsky/slp3/3.pdf
5. 贪心学院课程