C语言基础 递归的用法及示例

---------------start reading----------------

前言
递归在数学证明中经常使用，其意就是不停的套用同一模板逐渐归纳出最后的结果，用通俗的话来说就是自己调用自己。

递归调用需要注意三个问题

1. 缩小问题规模
2. 边界条件
3. 返回段

我们来看看递归的入门题
有五个人年龄不等
第五个人说，我比第四个人大两岁；
第四个人说，我比第三个人大两岁；
第三个人说，我比第二个人大两岁；
第二个人说，我比第一个人大两岁；

在以前我们可以用循环来实现，功能代码如下

int Age1(int n)//O(n),O(1)
{
	int age = 10;
	for(int i=1;i

现在我们来用递归实现，功能函数如下

int Age(int n)//O(n),O(n)
{
	int tmp;
	if(n == 1)
		tmp = 10;
	else
		tmp = Age(n-1) + 2;
	return tmp;
}

递归实现的思路其实是这样的
想要知道第五个人的年龄，就要先知道第四个人的年龄；
想要知道第四个人的年龄，就要先知道第三个人的年龄；
想要知道第三个人的年龄，就要先知道第二个人的年龄；
想要知道第二个人的年龄，就要先知道第一个人的年龄。
知道了第一个人的年龄就可以算出第二个人的年龄，进而算出第三个，第四个，最终得到第五个人的年龄

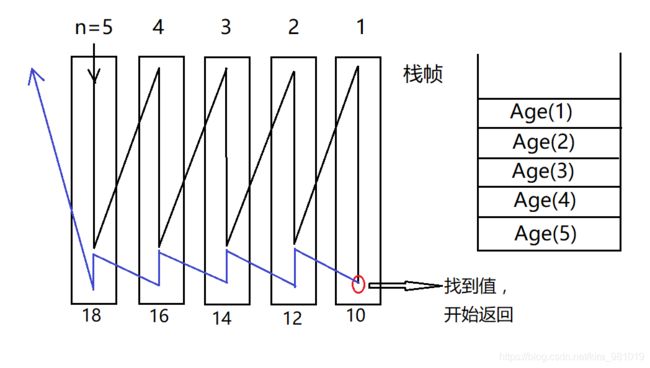
实现的物理模型如图

递归就是通过不停的压栈再出栈来实现问题规模缩小。有时候递归很方便，但是，递归也有很大的缺点，下面就让递归和循环进行一下比较，你就知道递归的弊处了

如上题所示代码
循环
时间复杂度：O（n）

空间复杂度：定义了变量age，i，O（2）

递归
时间复杂度：O（n）

空间复杂度：由于递归没有找到值就不会返回，所以递归进行时会不停的压栈，空间复杂度为O（n），空间使用率小

综上所述
递归虽然同循环的时间复杂度一样，但在空间利用率上却大大的跟不上。在windos中栈的空间只有1M，一个字符=两个字节如果数据稍微一大便会使程序崩溃。

接下来让我们来用递归写一写斐波那契数列的功能函数

int Fibno(int n)
{
	if(n==1 || n==2)
		return 1;
	else
		return Fibno(n-1)+Fibno(n-2);
}

经过调试，数据上40就很难调试出来，因为他用了很大的空间

但是也有适合使用递归的例子
汉诺塔问题，如何用最少的次数将三个圆环一道另一根柱子上且保持顺序不变

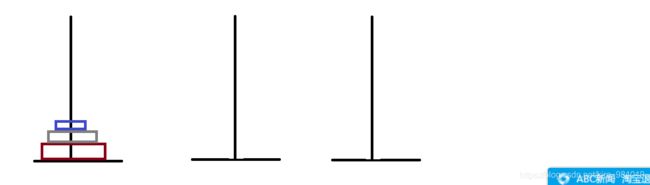
int g_count = 0;
void Move(char x,char y)
{
	g_count++;
	printf("%c->%c\n",x,y);
}

void Hanoi(int n,char a,char b,char c)
{
	if(n == 1)
	{
		Move(a,c);
	}
	else
	{
		Hanoi(n-1,a,c,b);//
		Move(a,c);
		Hanoi(n-1,b,a,c);
	}
}

int main()
{
	Hanoi(5,'A','B','C');
	printf("%d\n",g_count);
}
汉诺塔移动过程就可以用递归来实现，方便理解，而且在实际操作中也不会有太多的空间浪费，汉诺塔是最适合用递归的例子


---------------end---------------