手写体数字识别———LeNet模型
一,Minist数据集特点
MNIST 数据集来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST). 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员. 测试集(test set) 也是同样比例的手写数字数据.
简单地说,Minist数据集就是这些:
该数据集由四部分组成 ,也就是一个训练图片集,一个训练标签集,一个测试图片集,一个测试标签集(60,000 个训练样本和 10,000 个测试样本.)
例如下面是数字 7 的 25 个不同形态:
二,卷积神经网络LeNet-5详解
卷积神经网络: 是一种常见的深度学习架构,受生物自然视觉认知机制(动物视觉皮层细胞负责检测光学信号)启发而来,是一种特殊的多层前馈神经网络。它的人工神经元可以响应一部分覆盖范围内的周围单元,对于大型图像处理有出色表现。
一般神经网络VS卷积神经网络:
相同点:卷积神经网络也使用一种反向传播算法(BP)来进行训练
不同点:网络结构不同。卷积神经网络的网络连接具有局部连接、参数共享的特点。
(局部连接:是相对于普通神经网络的全连接而言的,是指这一层的某个节点只与上一层的部分节点相连。
参数共享:是指一层中多个节点的连接共享相同的一组参数。 )
(一)卷积神经网络的主要组成
卷积层(Convolutional layer),卷积运算的目的是提取输入的不同特征,第一层卷积层可能只能提取一些低级的特征如边 缘、线条和角等层级,更多层的网络能从低级特征中迭代提取更复杂的特征。
池化层(Pooling),它实际上一种形式的向下采样。有多种不同形式的非线性池化函数,而其中最大池化(Max pooling)和平均采样是最为常见的。pooling层的作用:Pooling层相当于把一张分辨率较高的图片转化为分辨率较低的图片; pooling层可进一步缩小最后全连接层中节点的个数,从而达到减少整个神经网络中参数的目的
全连接层(Full connection), 与普通神经网络一样的连接方式,一般都在最后几层
(二)Lenet-5卷积神经网络模型
LeNet-5:是Yann LeCun在1998年设计的用于手写数字识别的卷积神经网络,当年美国大多数银行就是用它来识别支票上面的手写数字的,它是早期卷积神经网络中最有代表性的实验系统之一。
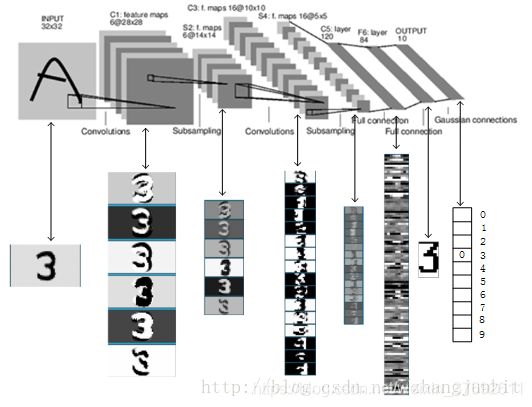
LenNet-5共有7层(不包括输入层),每层都包含不同数量的训练参数,主要有2个卷积层、2个下抽样层(池化层)、3个全连接层3种连接方式。如下图所示。
例如,下图是识别数字3的过程:
LeNet-5各层结构:
输入: 首先 是 数据输入 INPUT 输入图像的尺寸归一化为32*32
- C1层(卷积层)
第一层卷积层的输入为原始的图像,原始图像的尺寸为32×32×1。卷积层的过滤器尺寸为5×5,深度为6,不使用全0补充,步长为1。由于没有使用全0补充,所以这一层的输出的尺寸为32-5+1=28,深度为6。这一个卷积层总共有5×5×1×6+6=156个参数,其中6为偏置项参数个数,卷积层的参数个数只和过滤器的尺寸,深度以及当前层节点矩阵的深度有关。因为下一层节点矩阵有28×28×6=4704个节点,每个节点和5×5=25个当前层节点相连,所以本层卷积层总共有4704×(25+1)=122304个连接。但是我们只需要学习156个参数,主要是通过权值共享实现的。
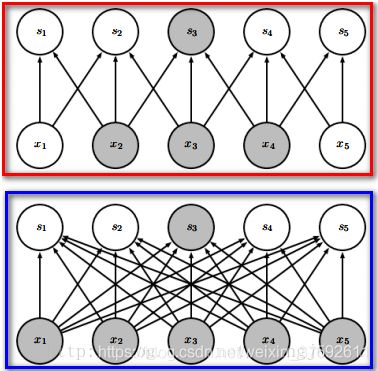
那么为什么要使用卷积呢?原因如下图(红色框是卷积网络,蓝色框中是全连接神经网络):
卷积相对于全连接是稀疏的。优势:1、参数更少 2、计算量降低。
2,S2层(池化层)
这一层的输入为第一层的输出,是一个28×28×6的节点矩阵。本层采用的过滤器大小为2×2,步长为2,所以本层的输出矩阵大小为14×14×6。
3,C3层(第二次卷积)
C3层是一个卷积层,卷积和和C1相同,不同的是C3的每个节点与S2中的多个图相连。 本层的输入矩阵大小为14×14×6,采用的过滤器大小为5×5,深度为16,不使用全0补充,步长为1。这一层的输出的尺寸为14-5+1=10,深度为16,即输出矩阵大小为10×10×16。本层参数有5×5×6×16+16=2416个,连接有10×10×16×(5×5+1)=41600个。
4,S4层(第二个池化层)
S4是pooling层,窗口大小仍然是2*2,共计16个feature map,C3层的16个10x10的图分别进行以2x2为单位的池化得到16个5x5的特征图。这一层有2x16共32个训练参数,5x5x5x16=2000个连接。连接的方式与S2层类似。
5,C5(全连接层)
本层的输入矩阵大小为5×5×16,在LeNet-5模型的论文中将这一层称为卷积层,但是因为过滤器的大小就是5×5,所以和全连接层没有区别,这里直接看成全连接层。本层输入为5×5×16矩阵,将其拉直为一个长度为5×5×16的向量,即将一个三维矩阵拉直到一维空间以向量的形式表示,这样才可以进入全连接层进行训练。本层的输出节点个数为120,所以总共有5×5×16×120+120=48120个参数
6,F6(全连接层)
F6层是全连接层。本层的输入节点个数为120个,输出节点个数为84个,对应于一个7x12的比特图,-1表示白色,1表示黑色,这样每个符号的比特图的黑白色就对应于一个编码。该层的训练参数和连接数是(120 + 1)x84=10164。ASCII编码图如下:
7,Output层(全连接层)
Output层也是全连接层,共有10个节点,分别代表数字0到9,且如果节点i的值为0,则网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式。假设x是上一层的输入,y是RBF的输出,则RBF输出的计算方式是:
上式w_ij 的值由i的比特图编码确定,i从0到9,j取值从0到7*12-1。RBF输出的值越接近于0,则越接近于i,即越接近于i的ASCII编码图,表示当前网络输入的识别结果是字符i。该层有84x10=840个参数和连接。
(三)Lenet训练算法步骤
Tensorflow训练Lenet-5模型的卷积网络包括两个过程,为前向传播过程和训练过程。前向传播过程与神经网络的前向传播过程一样通过训练数据的输入经过网络得出实际输出,训练过程就是不断调整网络的输出与实际输出的之间网络的权值和偏值从而使两者之间的相差达到最小。
LeNet-5的训练算法
训练算法与传统的BP算法差不多。主要包括4步,这4步被分为两个阶段:
第一阶段,向前传播阶段:
a)从样本集中取一个样本(X,Yp),将X输入网络;
b)计算相应的实际输出Op。
在此阶段,信息从输入层经过逐级的变换,传送到输出 层。这个过程也是网络在完成训练后正常运行时执行的过程。在此过程中,网络执行的是计算(实际上就是输入与每层的权值矩阵相点乘,得到最后的输出结果):
Op=Fn(…(F2(F1(XpW(1))W(2))…)W(n))
第二阶段,向后传播阶段
a)算实际输出Op与相应的理想输出Yp的差;
b)按极小化误差的方法反向传播调整权矩阵。
三,用Lenet实现手写体识别
Minist_inference.py(定义了前向传播的过程以及神经网络中的参数)
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import tensorflow as tf
# 定义神经网络相关的参数
INPUT_NODE = 784
OUTPUT_NODE = 10
LAYER1_NODE = 500
IMAGE_SIZE = 28
NUM_CHANNELS = 1
NUM_LABELS = 10
# 第一层卷积层的尺寸和深度
CONV1_DEEP = 32
CONV1_SIZE = 5
# 第二层卷积层的尺寸和深度
CONV2_DEEP = 64
CONV2_SIZE = 5
# 全连接层的节点个数
FC_SIZE = 512
# 定义神经网络的前向传播过程。
# 这里添加了一个新的参数train,用于区别训练过程和测试过程。
# 在这个程序中将用到dropout方法,dropout可以进一步提升模型可靠性并防止过拟合,dropout过程只在训练时使用。
def inference(input_tensor, train, regularizer):
# 声明第一层神经网络的变量并完成前向传播过程。这个过程和6.3.1小节中介绍的一致。
# 通过使用不同的命名空间来隔离不同层的变量,这可以让每一层中的变量命名只需要考虑在当前层的作用,而不需要担心重名的问题。
# 和标准LeNet-5模型不大一样,这里定义卷积层的输入为28*28*1的原始MNIST图片像素。
# 因为卷积层中使用了全0填充,所以输出为28*28*32的矩阵。
with tf.variable_scope('layer1-conv1'):
# 这里使用tf.get_variable或tf.Variable没有本质区别,因为在训练或是测试中没有在同一个程序中多次调用这个函数。
# 如果在同一个程序中多次调用,在第一次调用之后需要将reuse参数置为True。
conv1_weights = tf.get_variable(
"weight", [CONV1_SIZE, CONV1_SIZE, NUM_CHANNELS, CONV1_DEEP],
initializer = tf.truncated_normal_initializer(stddev=0.1)
)
conv1_biases = tf.get_variable("bias", [CONV1_DEEP], initializer=tf.constant_initializer(0.0))
# 使用边长为5,深度为32的过滤器,过滤器移动的步长为1,且使用全0填充
conv1 = tf.nn.conv2d(input_tensor, conv1_weights, strides=[1, 1, 1, 1], padding='SAME')
relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))
# 实现第二层池化层的前向传播过程。
# 这里选用最大池化层,池化层过滤器的边长为2,使用全0填充且移动的步长为2。
# 这一层的输入是上一层的输出,也就是28*28*32的矩阵。输出为14*14*32的矩阵。
with tf.name_scope('layer2-pool'):
pool1 = tf.nn.max_pool(relu1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# 声明第三层卷积层的变量并实现前向传播过程。
# 这一层的输入为14*14*32的矩阵,输出为14*14*64的矩阵。
with tf.variable_scope('layer3-conv2'):
conv2_weights = tf.get_variable(
"weight", [CONV2_SIZE, CONV2_SIZE, CONV1_DEEP, CONV2_DEEP],
initializer = tf.truncated_normal_initializer(stddev=0.1)
)
conv2_biases = tf.get_variable("bias", [CONV2_DEEP], initializer=tf.constant_initializer(0.0))
# 使用边长为5,深度为64的过滤器,过滤器移动的步长为1,且使用全0填充
conv2 = tf.nn.conv2d(pool1, conv2_weights, strides=[1, 1, 1, 1], padding='SAME')
relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))
# 实现第四层池化层的前向传播过程。
# 这一层和第二层的结构是一样的。这一层的输入为14*14*64的矩阵,输出为7*7*64的矩阵。
with tf.name_scope('layer4-poo2'):
pool2 = tf.nn.max_pool(relu2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# 将第四层池化层的输出转化为第五层全连接层的输入格式。
# 第四层的输出为7*7*64的矩阵,然而第五层全连接层需要的输入格式为向量,所以在这里需要将这个7*7*64的矩阵拉直成一个向量。
# pool2.get_shape函数可以得到第四层输出矩阵的维度而不需要手工计算。
# 注意因为每一层神经网络的输入输出都为一个batch的矩阵,所以这里得到的维度也包含了一个batch中数据的个数。
pool_shape = pool2.get_shape().as_list()
# 计算将矩阵拉直成向量之后的长度,这个长度就是矩阵长度及深度的乘积。
# 注意这里pool_shape[0]为一个batch中样本的个数。
nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]
# 通过tf.reshape函数将第四层的输出变成一个batch的向量。
reshaped = tf.reshape(pool2, [pool_shape[0], nodes])
# 声明第五层全连接层的变量并实现前向传播过程。
# 这一层的输入是拉直之后的一组向量,向量长度为7*7*64=3136,输出是一组长度为512的向量。
# 这一层和之前在第5章中介绍的基本一致,唯一的区别是引入了dropout的概念。
# dropout在训练时会随机将部分节点的输出改为0。
# dropout可以避免过拟合问题,从而使得模型在测试数据上的效果更好。
# dropout一般只在全连接层而不是卷积层或者池化层使用。
with tf.variable_scope('layer5-fc1'):
fc1_weights = tf.get_variable("weight", [nodes, FC_SIZE],
initializer = tf.truncated_normal_initializer(stddev = 0.1))
# 只有全连接层的权重需要加入正则化
if regularizer != None:
tf.add_to_collection('losses', regularizer(fc1_weights))
fc1_biases = tf.get_variable('bias', [FC_SIZE], initializer = tf.constant_initializer(0.1))
fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_weights)+fc1_biases)
if train:
fc1 = tf.nn.dropout(fc1, 0.5)
# 声明第六层全连接层的变量并实现前向传播过程。
# 这一层的输入是一组长度为512的向量,输出是一组长度为10的向量。
# 这一层的输出通过Softmax之后就得到了最后的分类结果。
with tf.variable_scope('layer6-fc2'):
fc2_weights = tf.get_variable("weight", [FC_SIZE, NUM_LABELS],
initializer = tf.truncated_normal_initializer(stddev = 0.1))
if regularizer != None:
tf.add_to_collection('losses', regularizer(fc2_weights))
fc2_biases = tf.get_variable('bias', [NUM_LABELS], initializer = tf.constant_initializer(0.1))
logit = tf.matmul(fc1, fc2_weights) + fc2_biases
# 返回第六层的输出
return logitMinist_train.py(定义了神经网络的训练过程)
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import os
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 加载mnist_inference.py中定义的常量和前向传播的函数
import mnist_inference
# 配置神经网络的参数
BATCH_SIZE = 100
LEARNING_RATE_BASE = 0.01
LEARNING_RATE_DECAY = 0.99
REGULARAZTION_RATE = 0.0001
TRAINING_STEPS = 30000
MOVING_AVERAGE_DECAY = 0.99
# 模型保存的路径和文件名
MODEL_SAVE_PATH = "model/"
MODEL_NAME = "model.ckpt"
def train(mnist):
# 定义输入输出placeholder
# 调整输入数据placeholder的格式,输入为一个四维矩阵
x = tf.placeholder(tf.float32, [
BATCH_SIZE, # 第一维表示一个batch中样例的个数
mnist_inference.IMAGE_SIZE, # 第二维和第三维表示图片的尺寸
mnist_inference.IMAGE_SIZE,
mnist_inference.NUM_CHANNELS], # 第四维表示图片的深度,对于RBG格式的图片,深度为5
name='x-input')
y_ = tf.placeholder(tf.float32, [None, mnist_inference.OUTPUT_NODE], name='y-input')
regularizer = tf.contrib.layers.l2_regularizer(REGULARAZTION_RATE)
# 直接使用mnist_inference.py中定义的前向传播过程
y = mnist_inference.inference(x, True, regularizer)
global_step = tf.Variable(0, trainable=False)
#定义损失函数、学习率、滑动平均操作以及训练过程
variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
variable_averages_op = variable_averages.apply(tf.trainable_variables())
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
cross_entropy_mean = tf.reduce_mean(cross_entropy)
loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step, mnist.train.num_examples/BATCH_SIZE, LEARNING_RATE_DECAY)
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
with tf.control_dependencies([train_step, variable_averages_op]):
train_op = tf.no_op(name='train')
# 初始化Tensorflow持久化类
saver = tf.train.Saver()
with tf.Session() as sess:
tf.global_variables_initializer().run()
# 验证和测试的过程将会有一个独立的程序来完成
for i in range(TRAINING_STEPS):
xs, ys = mnist.train.next_batch(BATCH_SIZE)
#类似地将输入的训练数据格式调整为一个四维矩阵,并将这个调整后的数据传入sess.run过程
reshaped_xs = np.reshape(xs, (BATCH_SIZE, mnist_inference.IMAGE_SIZE, mnist_inference.IMAGE_SIZE, mnist_inference.NUM_CHANNELS))
_, loss_value, step = sess.run([train_op, loss, global_step], feed_dict={x: reshaped_xs, y_: ys})
#每1000轮保存一次模型。
if i%1000 == 0:
# 输出当前的训练情况。这里只输出了模型在当前训练batch上的损失函数大小。通过损失函数的大小可以大概了解训练的情况。
# 在验证数据集上的正确率信息会有一个单独的程序来生成。
print("After %d training step(s), loss on training batch is %f." % (step, loss_value))
# 保存当前的模型。注意这里隔出了global_step参数,这样可以让每个被保存模型的文件名末尾加上训练的轮数,比如“model.ckpt-1000”表示训练1000轮后得到的模型
saver.save(sess, os.path.join(MODEL_SAVE_PATH, MODEL_NAME), global_step=global_step)
def main(argv=None):
mnist = input_data.read_data_sets("dataset/", one_hot=True)
train(mnist)
if __name__ == '__main__':
tf.app.run()mnist_eval.py (定义了测试过程)
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import time
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 加载mnist_inference.py 和 mnist_train.py中定义的常量和函数
import mnist_inference
import mnist_train
# 每10秒加载一次最新的模型, 并在测试数据上测试最新模型的正确率
EVAL_INTERVAL_SECS = 10
def evaluate(mnist):
with tf.Graph().as_default() as g:
# 定义输入输出的格式
x = tf.placeholder(tf.float32, [
mnist.validation.num_examples, # 第一维表示样例的个数
mnist_inference.IMAGE_SIZE, # 第二维和第三维表示图片的尺寸
mnist_inference.IMAGE_SIZE,
mnist_inference.NUM_CHANNELS], # 第四维表示图片的深度,对于RBG格式的图片,深度为5
name='x-input')
y_ = tf.placeholder(tf.float32, [None, mnist_inference.OUTPUT_NODE], name='y-input')
validate_feed = {x: np.reshape(mnist.validation.images, (mnist.validation.num_examples, mnist_inference.IMAGE_SIZE, mnist_inference.IMAGE_SIZE, mnist_inference.NUM_CHANNELS)),
y_: mnist.validation.labels}
# 直接通过调用封装好的函数来计算前向传播的结果。
# 因为测试时不关注正则损失的值,所以这里用于计算正则化损失的函数被设置为None。
y = mnist_inference.inference(x, False, None)
# 使用前向传播的结果计算正确率。
# 如果需要对未知的样例进行分类,那么使用tf.argmax(y, 1)就可以得到输入样例的预测类别了。
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 通过变量重命名的方式来加载模型,这样在前向传播的过程中就不需要调用求滑动平均的函数来获取平局值了。
# 这样就可以完全共用mnist_inference.py中定义的前向传播过程
variable_averages = tf.train.ExponentialMovingAverage(mnist_train.MOVING_AVERAGE_DECAY)
variable_to_restore = variable_averages.variables_to_restore()
saver = tf.train.Saver(variable_to_restore)
#每隔EVAL_INTERVAL_SECS秒调用一次计算正确率的过程以检测训练过程中正确率的变化
while True:
with tf.Session() as sess:
# tf.train.get_checkpoint_state函数会通过checkpoint文件自动找到目录中最新模型的文件名
ckpt = tf.train.get_checkpoint_state(mnist_train.MODEL_SAVE_PATH)
if ckpt and ckpt.model_checkpoint_path:
# 加载模型
saver.restore(sess, ckpt.model_checkpoint_path)
# 通过文件名得到模型保存时迭代的轮数
global_step = ckpt.model_checkpoint_path.split('/')[-1].split('-')[-1]
accuracy_score = sess.run(accuracy, feed_dict = validate_feed)
print("After %s training step(s), validation accuracy = %f" % (global_step, accuracy_score))
else:
print("No checkpoint file found")
return
time.sleep(EVAL_INTERVAL_SECS)
def main(argv=None):
mnist = input_data.read_data_sets("dataset/", one_hot=True)
evaluate(mnist)
if __name__ == '__main__':
tf.app.run()实验结果:
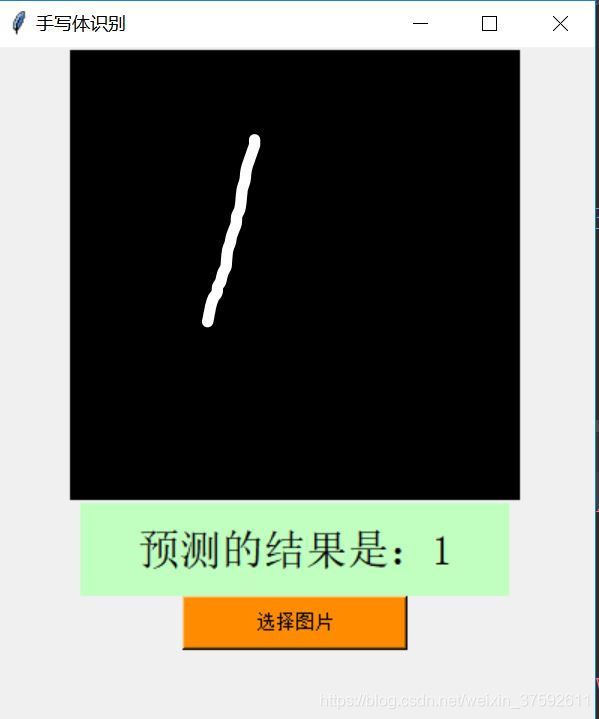 图1
图1
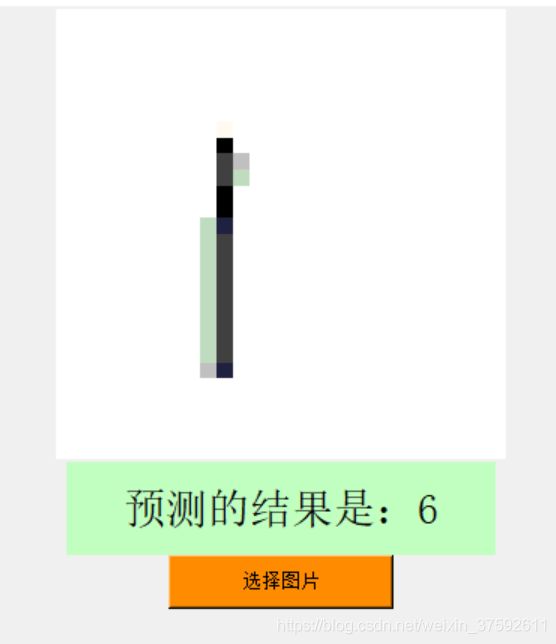 图2
图2
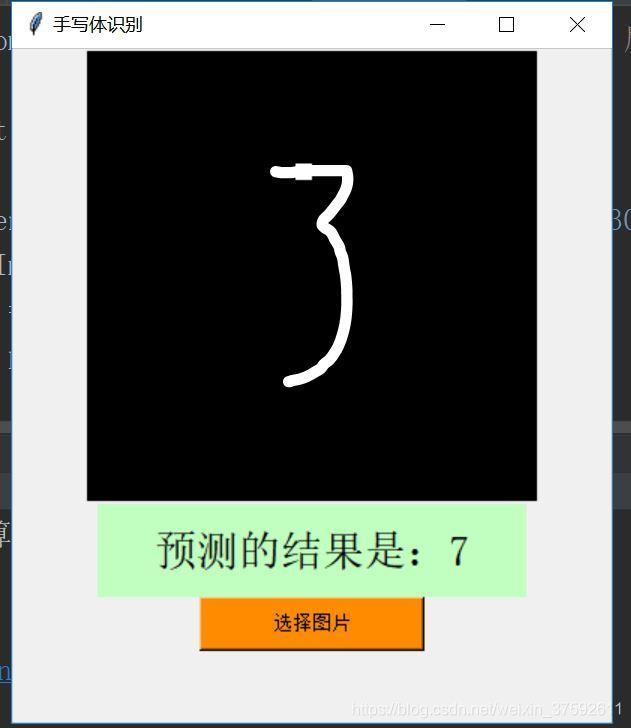 图3
图3
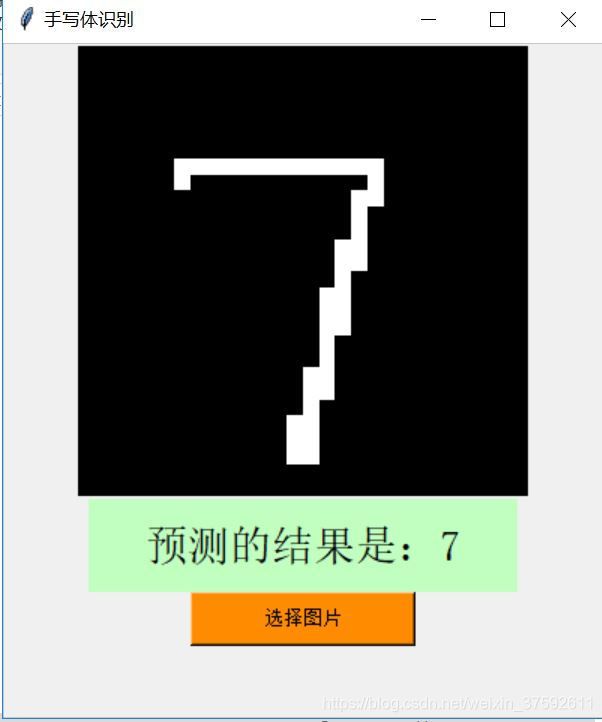 图4
图4
 图5
图5
 图6
图6
当学习率等于0.8时,每次训练的损失值
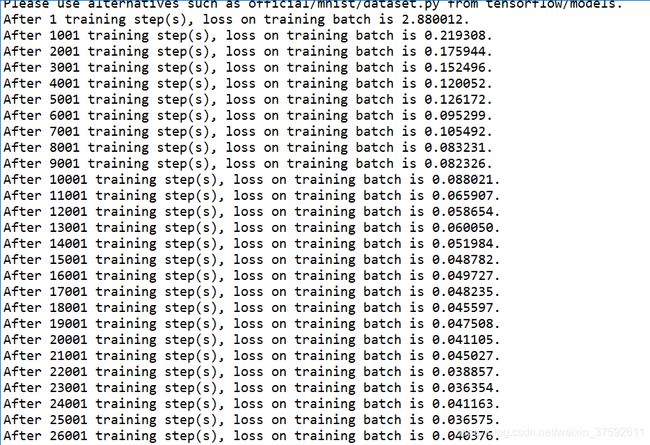
当学习率等于0.01时,每次训练的损失值
四,实验总结
本实验中每次batch的数量为100,batch表示一次迭代训练数据量的大小;batchsize越小,一个batch中的随机性越大,越不易收敛。然而batchsize越小,速度越快,权值更新越频繁;且具有随机性,对于非凸损失函数来讲,更便于寻找全局最优。从这个角度看,收敛更快,更容易达到全局最优。batchsize越大,越能够表征全体数据的特征,其确定的梯度下降方向越准确,(因此收敛越快),且迭代次数少,总体速度更快。然而大的batchsize相对来讲缺乏随机性,容易使梯度始终向单一方向下降,陷入局部最优;而且当batchsize增大到一定程度,再增大batchsize,一次batch产生的权值更新(即梯度下降方向)基本不变。
神经网络权值和偏值的调整与梯度的下降方向和速度有关,用梯度下降算法乘以学习率可以计算下一个定点的位置。当LEARNING_RATE_BASE=0.8时,由于初始学习率过大,损失函数的输出值较大说明输出值与实际值差别较大,测试结果准确率较低。当LEARNING_RATE_BASE=0.01时,损失函数的输出值较小,说明输出值与实际差别较小,测试结果较为准确。由实验可知,当学习率较大时,神经网络的学习速度较快但是容易导致损失值爆炸,振荡无法拟合,误差大;当学习率较小时,神经网络的学习速度较慢,损失值较小与实际的输出较为接近,但是学习率较小容易导致过渡拟合,无法快速地找到好的下降方向,随着迭代次数的增大损失值基本不变。
本实验中发现该神经网络对minist数据集本身的测试图像识别的准确率较高,如上图6为minist本身自带的图片;可能由于该卷积神经网络的结构设置的不够合理,导致过拟合现象。同时,对比图1和图2,图4和图5发现,在输入图像的背景为黑色时识别的效果较好;原因可能时用于该背景与测试图像的背景相同,同时可能用于实验测试的图像要转化为位图导致图像质量的损失而导致图像的别率较低。对比图3和图4,数字3被识别为7,从图像上看出数字3写的有点类似与7,所以在识别过程中被误认为7.
虽然卷积神经网络的结构比全连接神经网络结构简化了,但是卷积神经网络的计算量还是很大的,在本次实验中训练就用了一天多(cpu).但实际用自己手写的字体测试效果还不是很好。