Matlab之BP神经网络反向传播算法
(1)BP算法
Matlab中集成有BP算法工具箱,而且性能稳定,比较实用。这里不采用matlab自带工具箱,而是通过编写反向传播算法直接来实现,旨在能更好的从理论上来理解BP神经网络算法以及一些参数对算法的影响,再就是理解到反向传播的整个过程。其中部分程序参考论坛牛人们的编程方式来实现的。
(2)问题描述
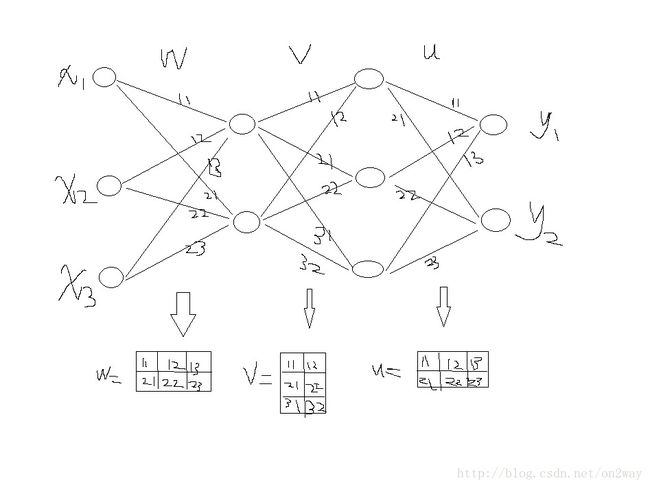
BP算法一般都是用来对数据进行分类和建立预测模型的,这里,我是来进行数据分类,通过改变训练权值来实现分类。问题中,选取3个输入量和2个输出量,并模拟生成100组这样的输入输出量。对BP网络的建立,要明确的是自己建立几层网络,有几层隐含层,每层有多少个节点等等,弄清楚了网络的具体结构才有助于分析它的性能。这里我们选取包含2层隐含层的四层网络结构,再根据输入输出量的个数就很容易想想出需要建立的网络模型了吧,如下图所示:
网络的结果以及权值规定分别如上图所示,有了这样,我们才能对各层与层之间的权值进行赋值与计算。
图中画出的是大致结构,了解BP算法原理的应该知道,对于每个节点的输出还要采取一个激励函数处理(典型的是sigmoid函数),经过这个函数处理后的输出才能作为下一层的节点输入量。至于为什么要要这个激励函数,而为什么不直接用w*x的权值和代替,首先sigmoid函数处理后可以把对应的输出值限制在0~1之间,再有就是的的导数性质了,详细原因可以去看专门介绍原理的文章。那么这样的话,每个节点的详细传播公式就应该如下所示:
(3)算法介绍
算法伪代码如下所示(摘自机器学习P72):
不过该图给出的是只含一层隐含层的伪代码,和我们这里的两层隐含层略有不同,需要多计算一次对应的delta值。
(4)输入与输出量
function d = datafile() %初始城市距离
x1=[29,43,50,36,2,29,94,45,83,93,41,76,39,91,45,28,28,39,57,...
72,12,38,52,83,32,15,100,49,83,93,50,45,72,56,36,43,11,...
23,67,67,2,86,14,92,51,52,94,55,87,40,14,30,24,22,17,22,...
7,43,71,23,32,33,53,32,27,94,19,54,76,50,67,53,2,45,73,98,...
19,15,9,24,64,51,62,86,58,32,53,45,52,85,84,29,83,67,91,45,71,8,76,99];
x2=[54,47,65,79,56,80,55,65,85,67,67,42,45,56,21,67,72,50,33,2,...
81,55,66,13,30,63,55,7,39,19,61,43,35,69,45,69,39,83,50,60,...
44,10,56,99,59,17,66,68,41,83,26,42,79,0,14,48,44,96,65,37,...
61,85,72,40,24,82,0,44,58,35,43,28,67,58,37,28,34,40,61,45,...
22,28,60,91,81,51,83,75,97,91,58,83,68,57,55,38,87,59,100,80];
x3=[98,56,31,78,30,90,73,52,37,21,93,97,25,60,90,66,28,69,46,67,...
32,56,95,6,1,86,52,89,61,26,82,97,52,43,39,95,59,2,22,6,83,...
91,0,51,76,94,45,37,11,40,9,12,7,19,60,38,17,76,55,89,91,44,...
18,55,24,73,32,29,75,9,69,95,84,69,58,59,93,37,1,57,84,75,17,...
70,40,6,86,11,71,64,95,19,21,17,3,79,33,41,19,42];
y1=[973,202,77,541,59,796,429,187,131,63,853,938,40,256,738,335,77,357,...
114,308,100,210,906,10,12,677,181,710,250,30,594,936,160,133,83,909,...
222,71,42,43,591,763,33,240,479,839,144,102,27,137,9,22,65,9,220,80,...
25,535,216,721,794,161,63,186,22,466,35,49,463,18,354,871,638,367,216,...
223,818,68,38,208,604,435,47,434,135,29,710,62,457,353,899,79,64,44,...
39,512,119,105,114,148];
y2=[63,107,170,117,34,97,868,139,648,851,123,466,82,791,105,73,77,91,201,...
380,71,91,194,574,42,52,1035,127,593,811,170,119,391,228,71,137,22,81,...
328,337,28,646,34,882,175,153,879,216,676,137,10,46,77,13,13,37,21,179,...
406,35,79,113,203,54,28,905,10,180,480,138,326,166,53,132,409,955,28,23,...
38,40,275,148,276,726,265,59,226,148,242,703,636,95,620,335,784,113,...
437,39,541,1038];
for i=1:length(y1)
s1(i)=1/(1+exp(-y1(i)));%对输出进行尺度调整至(0,1)范围
s2(i)=1/(1+exp(-y2(i)));
end
data = [x1;x2;x3;s1;s2];
save data.mat data;上述数据即为对应的输入与输出量,对于最后几行,对y值进行范围处理,可不可以不处理,如果不处理的话会发现效果很差,为什么,因为对于你计算的输出来说,那些值就是经过sigmoid函数处理出来的,这里这样处理以后在数值上也化为相同范围了,否则,你的目标输出都在100左右,而你的计算输出都在0~1左右,这样根本没法比,会一直存在误差。
(5)程序代码
%-------------函数说明----------------
% 交换地点顺序
% 输入变量:
% training_example:待训练的数据
% eta: 学习速率
%---------------------------------------
function BP_BACK(training_example,eta)
[m,n] = size(training_example); %m--行,n--列
%初始化权值矩阵-0.5~0.5之间
w = rand(2,3) - 0.5;
v = rand(3,2) - 0.5;
u = rand(2,3) - 0.5;
%------------------------
for num = 1:n %对每组输入量与输出量
%%----------------------------------------
one_sample = training_example(:,num); %取一组
x = one_sample(1:3); %提取其中的输入
y = one_sample(4:5); %提取其中的输出
net2 = w * x; %第一层求和值
for i=1:2
hidden1(i)=1/(1+exp(-net2(i)));%进行sigmoid处理输出
end
net3 = v * hidden1'; %第二层求和值
for i=1:3
hidden2(i)=1/(1+exp(-net3(i)));%进行sigmoid处理输出
end
net4 = u * hidden2'; %第三层求和值
for i=1:2
o(i)=1/(1+exp(-net4(i)));%sigmoid处理输出,最终的输出值o
end
%%-------------反向传播算法,计算各层delta值(误差E对各层权值的导数)-----------------
%最后一层delta值
for i = 1:2
delta3(i) = (y(i)-o(i))*o(i)*(1-o(i)); %计算公式
end
%-----第二个隐含层---
for j = 1:3 %计算公式,与其后一层的delta值相关
delta2(j) = hidden2(j)*(1-hidden2(j))*delta3*u(:,j);
end
%-----第一个隐含层---
for k = 1:2 %计算公式,与其后一层的delta值相关
delta1(k) = hidden1(k)*(1-hidden1(k))*delta2*v(:,k);
end
%---------------------------------------------------------
%--------各层delta计算完后开始更新权值---------------------
%---更新u权值-----
for i = 1:2
for j = 1:3 %计算公式 w = w + eta*delta*x
u(i,j) = u(i,j) + eta*delta3(i)*hidden2(j);
end
end
%---更新v权值-----
for i = 1:3
for j = 1:2
v(i,j) = v(i,j) + eta*delta2(i)*hidden1(j);
end
end
%---更新w权值-----
for i = 1:2
for j = 1:3
w(i,j) = w(i,j) + eta*delta1(i)*x(j);
end
end
%---------------------------------------------------------
%--------------记录一下这个过程后的误差值
e=o'-y;%计算误差向量 (计算输出-目标输出)
sigma(num)=e'*e;%计算误差平方和
end
%%-------------------------------------------------------
plot(sigma);(6)运行结果
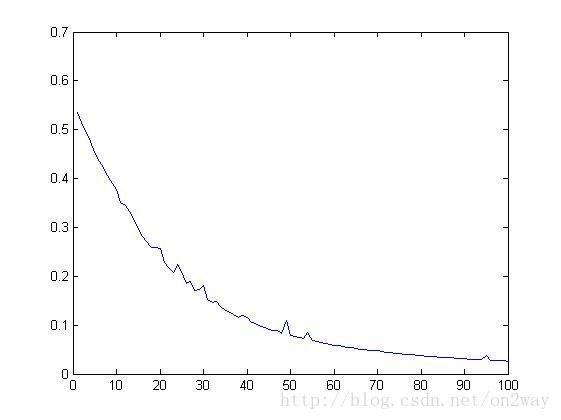
对上述给出的数据加载到matlab工作框中,设置好学习速率,然后直接运行BP_BACK函数可以得到误差函数曲线如下:
>>BP_BACK(data,0.5)
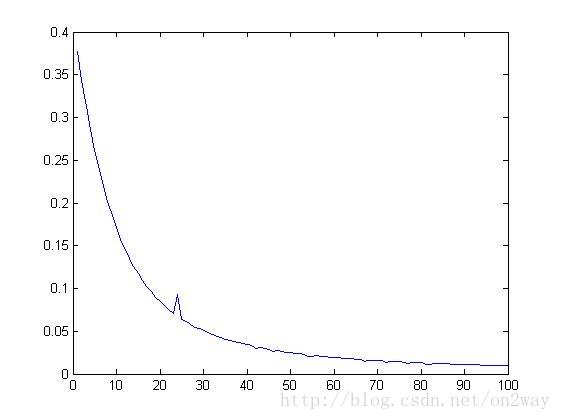
>>BP_BACK(data,0.9)
上述可以看出,随着数据的输入,迭代过程中输入与输出结果的误差是在不停的减小的,说明权值更新的效果较好。