Identity Mappings in Deep Residual Networks
引言
ResNet来自2015年he等人的paper:Deep Residual Learning for Image Recognition,在应对神经网络的退化上表现得非常出色。本文是在前文的基础上,对resnet为何能够有效的原因进行进一步的分析并且对原始模型结构进行调整,原文地址:Identity Mappings in Deep Residual Networks。
从经验上来说,随着神经网络层数的增加,模型可以进行更加复杂的特征抽取,理论上模型能够取得更好的结果,但实际上随着层数的增加,模型出现了退化的现象:

可以看到,56层的模型效果还比不上20层的,但这并不是过拟合的原因,可以看到56层模型的训练误差要比26层的还要高,所以这是一个很让人疑惑的事情。
从理论出发,浅层网络应该包含在深层网络的解空间之中,也就是深层网络如果能够寻找到浅层网络这个解,最差也能达到浅层网络的效果。换个说法,假设深层网络中比浅层网络多出的那些层,都用来拟合一个恒等变换,此时的深层网络其实就是浅层网络,所以深层网络的退化现象其实是一个优化问题,模型无法找到最优的解。
模型
假设网络输入是 x x x,输出是 F ( x ) F(x) F(x),拟合的目标是 H ( x ) H(x) H(x),正常情况下网络拟合的目标是 F ( x ) = H ( x ) F(x)=H(x) F(x)=H(x)。
现在需要拟合一个恒等变换,即希望 F ( x ) = x F(x)=x F(x)=x,作者提到让多个非线性函数拟合一个恒等变换是比较困难的,从上述结果也可以看到深层网络表现比较差。
所以,残差网络改变了拟合的目标,即把输出 F ( x ) F(x) F(x)与输入 x x x相加,将 F ( x ) + x F(x)+x F(x)+x作为最终的输出,训练目标是 F ( x ) = H ( x ) − x F(x)=H(x)-x F(x)=H(x)−x,因此得名残差网络。从这里可以看到,假如需要拟合一个恒等变换,其实网络拟合的目标是 F ( x ) = 0 F(x)=0 F(x)=0,由于神经网络的初始化参数就在0附近,这比前者要容易得多。
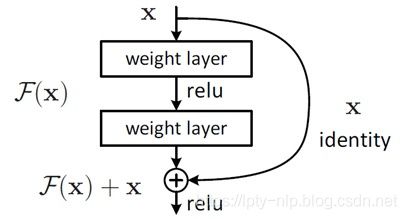
上述模型的公式如下所示:
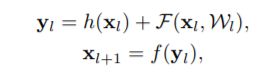
其中 x l x_l xl和 x l + 1 x_{l+1} xl+1是第 l l l个单元的输入和输出, W l = { W l , k ∣ 1 ≤ k ≤ K } W_l=\{W_l,k|1≤k≤K\} Wl={Wl,k∣1≤k≤K}是一组与第 l l l个残差单元相关的权重(偏置项), K K K是每一个残差单元中的层数(He2016中 K K K为2或者3), F F F表示一个残差函数,形如He2016中两个3×3卷积层的堆叠。在He2016中, h ( x l ) = x l h(x_l)=x_l h(xl)=xl 代表一个恒等映射, f f f代表 R e L U ReLU ReLU。
如果我们让形如 f f f也成为一个恒等变换,即 x l + 1 = y l x_{l+1}=y_l xl+1=yl,那么:
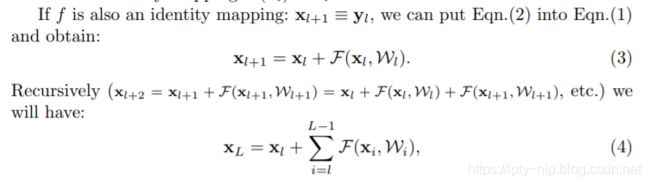
由上公式可以知道,对于任意深的单元 L L L的特征 X L X_L XL,都可以表达为浅层单元 l l l的特征 x l x_l xl加上一个形如 ∑ i = l L − 1 F \sum^{L−1} _{i=l}F ∑i=lL−1F的残差函数,这表明了任意单元 L L L和 l l l之间都具有残差特性。
同时对于任意深的单元 L L L,它的特征 x L = x 0 + ∑ i = 0 L − 1 F ( x i , W i ) x_L=x_0+\sum^{L−1}_{i=0}F(x_i,W_i) xL=x0+∑i=0L−1F(xi,Wi),即为之前所有残差函数输出的总和(加上 x 0 x_0 x0)。
利用链式规则,可以求得反向过程的梯度:
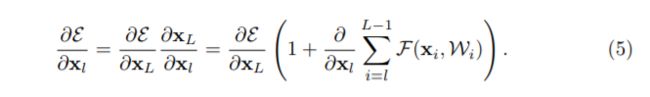
由上面可以看到,梯度 ∂ E ∂ x l \frac{\partial E}{\partial {{x}_{l}}} ∂xl∂E被分解成两个部分:
(1) ∂ E ∂ x L \frac{\partial E}{\partial {{x}_{L}}} ∂xL∂E直接传递信息而不涉及任何权重层,保证了信息能够直接回传到任意浅层 l l l。
(2) ∂ E ∂ x L ( ∂ ∑ i = l L − 1 F ∂ x l ) \frac{\partial E}{\partial {{x}_{L}}}\left(\frac{\partial {\sum_{i=l}^{L-1}\mathcal{F}}}{\partial {{x}_{l}}}\right) ∂xL∂E(∂xl∂∑i=lL−1F)表示通过权重层的传递,同时因为一个mini-batch中梯度不可能全为-1,保证了模型不会出现梯度消失的现象。
在前面的公式推导中,我们假设了两个恒等变换,即 h ( x l ) h(x_l) h(xl)和 f ( y l ) f(y_l) f(yl)。在前向和反向阶段,信号可以直接的从一个单元传递到其他任意一个单元。在文章中作者也用实验证明了,当模型接近这两种状态时,都能够取得较为不错的结果。
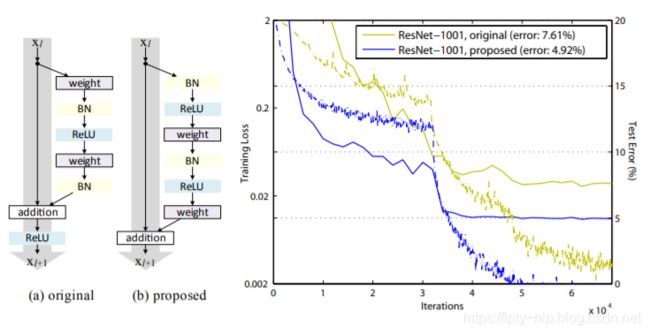
上述模型中(a)为He2016中提出的结构,(b)为本文经过实验最终得到的新结构,可以看到,新的结构在正确率上有了很明显的提升。
分析
前面提到恒等变换 h ( x l ) = x l h(x_l)=x_l h(xl)=xl和 f ( y l ) = y l f(y_l)=y_l f(yl)=yl对模型有明显的提升,下面分别分析这两个条件起到的作用。
Importance of Identity Skip Connections
设计一个更加通用的变换 h ( x l ) = λ l x l h({x}_{l}) = \lambda_l{x}_{l} h(xl)=λlxl,当 λ = 1 \lambda=1 λ=1时即为前述的恒等变换:
![]()
这里依旧认为 f f f为恒等变换,那么:
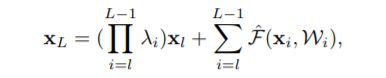
对上述公式进行链式求导,可得:
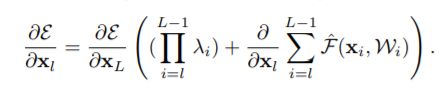
由上面的梯度公式可以知道,梯度 ∂ E ∂ x l \frac{\partial E}{\partial {{x}_{l}}} ∂xl∂E中的第一项受因子 λ \lambda λ的影响极大,对于一个极深的网络( L L L很大),如果对于所有的i都有 λ i > 1 \lambda_i>1 λi>1,那么这个因子将会是指数型的放大;
如果 λ i < 1 \lambda_i<1 λi<1,那么这个因子将会是指数型的缩小或者是消失,从而阻断从捷径反向传来的信号,并迫使它流向权重层。
通过实验也证明了这会使得优化出现困难。同样的,将 h ( x ) h(x) h(x)表示为更加复杂的变换(例如门控和1×的卷积),也会造成信息传递的阻碍,导致模型效果下降:
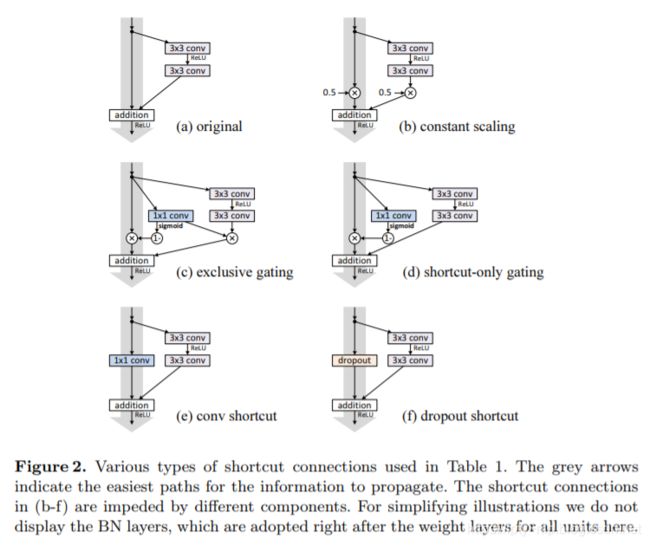
具体门控的形式这里不做解释,详细请看原论文,下面是对应的实验结果:
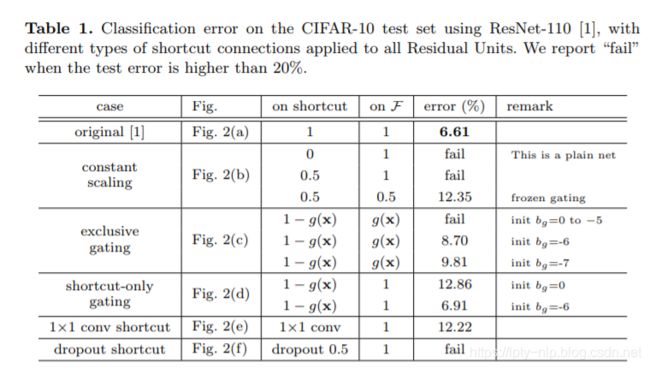
由上面的实验可以知道,捷径连接是信息传递最直接的路径。 捷径连接中的操作 (缩放、门控、1×1 的卷积以及 dropout) 会阻碍信息的传递,以致于对优化造成困难。
值得注意的是1×1的卷积捷径连接引入了更多的参数,本应该比恒等捷径连接具有更加强大的表达能力。事实上,shortcut-only gating 和1×1的卷积涵盖了恒等捷径连接的解空间。然而,它们的训练误差比恒等捷径连接的训练误差要高得多,这表明了这些模型退化问题的原因是优化问题,而不是表达能力的问题。
Importance of Activation Functions
同样的对于假设中的第二个恒等变换 f f f,依旧设计不同的方式进行实验,结果如下:

图e中的结构最后取得了最好的实验结果,这种方式是通过将传统的post-activate换成了pre-activate,即将激活函数和bn提前,构造出在F函数端的恒等变换。
结论
作为继Resnet的第二篇论文,这里用实验的方式展示了为何残差网络在深层模型中效果好的原因,同时也提出了效果更好的网络结构。
残差网络虽然是在为了处理图像领域的问题提出来的,但对于NLP的问题也同样适用。
引用
1、Deep Residual Learning for Image Recognition
2、Identity Mappings in Deep Residual Networks