线段树基本操作

线段树主要思想用二分区间的形式，以空间换时间降低时间复杂度，建树时间复杂度为nlog（n），查询时间复杂度为log（n）：

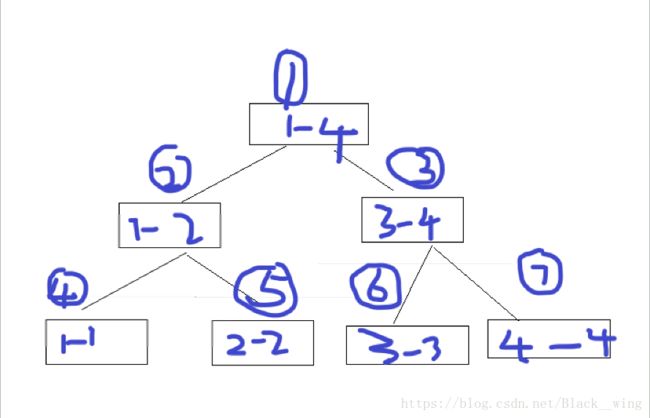
通常建树时用数组模拟链表建树，即获得上图样式线段树，从最大的区间二分，到两个小区间，然后小区间再二分直到得到l==r，即代表一点的区间（例如：1-1）这样的区间，对于数组模拟线段树，我们可以得到他们在我们树数组中的位置，即图中每个框上面圆圈中的数字。这样可以帮助我们快速调用最大的区间中我们想要获得的值。

下面附数组模拟指针建树的模板;

int tr[M*4];
void pushup(int i)
{
       tr[i]=tr[i*2+1]+tr[i*2];//此处可根据需要作出调整，最大值，最小值，求和等等。
       tr[i]=max(tr[i*2+1],tr[i*2]);//最大值
}
void build(int i,int l,int r)
{
    if(l==r)
    {
        scanf("%d",&tr[i]);
    }
    int mid=(r+l)/2;
    build(i*2,l,mid);
    build(i*2+1,mid+1,r);
    pushup(i);
}

更新区间模板:

void update(int i,int l,int r,int x,int k)
{
    if(l==r)
    {
        tr[i]=tr[i]+k;
        return;
    }
    int mid=(r+l)>>1;
    if(x<=mid)update(i*2,l,mid,x,k);
    if(y>mid) update(i*2+1,mid+1,r,x,k);
    pushup(i);
}

询问模板：

ll query(int i,int l,int r,int x,int y)
{
    ll ans=0;
    if(x<=l&&y>=r)
    {
        return tr[i];
    }
    int mid=(r+l)/2;
    if(x<=mid)ans+=query(i*2,l,mid,x,y);
    if(y>mid) ans+=query(i*2+1,mid+1,r,x,y);
    return ans;
}

线段树单点修改，区间更新例题：

hdu-2795：

对于此题，需要求出该广告可放置在哪一层，此题，可用线段树维护一个区间剩余空间的最大值，那么对于这个题，区间大小的确认我认为是很关键的。我们可以看到给我们的广告数为n=2e5，而高度h=1e9，每个广告的高度都为1。我们假设所有广告都能贴上需要的最大空间为n，如果有的广告贴不上，就说明hn时，维护区间1-n，其次h

下面附解题代码:

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define ll long long
using namespace std;
const int M=2e5+10;
int tr[M*4],w,h,n;
void pushup(int i)
{
    tr[i]=max (tr[i*2],tr[i*2+1]);
}
void build(int i,int l,int r)
{
    if(l==r)
    {
        tr[i]=w;
        return;
    }
    int mid =(r+l)/2;
    build(i*2,l,mid);
    build(i*2+1,mid+1,r);

    pushup(i);
}
int update(int i,int l,int r,int x)
{
    int ans;
    if(l==r)
    {
        tr[i]-=x;
        return l;
    }
    int mid=(r+l)/2;
    if(tr[i*2]>=x)
    {
        ans=update(i*2,l,mid,x);
    }
    else
    {
        ans=update(i*2+1,mid+1,r,x);
    }
    pushup(i);
    return ans;

}
int main()
{
    while(~scanf("%d%d%d",&h,&w,&n))
    {
        build(1,1,min(n,h));
        for(int i=1;i<=n;i++)
        {
            int x;
            scanf("%d",&x);
            if(tr[1]