Burnside引理与Polya定理

Burnside引理与Polya定理

Burnside引理与Polya定理是有关组合数学的两条十分重要的定理（引理）,但是网上的一些资料大多晦涩难懂或者与实际并不相关联，因此在这里做一些浅显的解读，希望通过此文章可以让这两条定理（引理）能够发挥其作用。

PS:引理与定理的区别:

Ψ引理是数学中为了取得某个更好的定理而作为步骤被证明的命题,其意义并不在于自身被证明,而在于为达成最终定理作出贡献.
Ψ一个引理可用于证明多个定理.数学中存在很多著名的引理,这些引理可能对很多问题的解决有帮助.例如欧几里得引理等。

Burnside引理：

提到这个引理的人：

·1845年德国法国数学家Cauchy
·1887年德国数学家Frobenius
·1897年英国数学家Burnside
·1937年匈牙利数学家Polya

Burnside引理的众多名称：

·轨道计数定理
·Burnside计数定理
·Cauchy—Frobenius引理
·Polya—Burnside引理

定义：

设G={a1,a2,…ag}是目标集[1,n]上的置换群。每个置换都写成不相交循环的乘积。是在置换ak的作用下不动点的个数，也就是长度为1的循环的个数。通过上述置换的变换操作后可以相等的元素属于同一个等价类。
若G将[1,n]划分成l个等价类，则：
等价类个数为： —— [ 百度百科 ]

理解：

如果上面看不懂没关系，下面我们来用几个例子来体会一下：
一正方形分成4格，2着色，有多少种方案？其中，经过转动相同的图象算同一方案。
解析：
对于每种格子我们都有两种选择，所以会有一下16种方案：

但是对于这16种方案可以归一下类：
Θ不动：a1=(1)(2)…(16)
Θ逆时针转90度 ：a2=(1)(2)(3 4 5 6)(7 8 9 10) (11 12)(13 14 15 16)
Θ顺时针转90度 ：a3=(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13)
Θ转180度：a4=(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12) (13 15)(14 16)
（a,b,c）表示a,b,c可以通过旋转得到。

由Burnside引理，共有(16+2+2+4)/4=6(种方案)

这里的4就是题目中的“置换群”，也就是我们分的类，而括号里的加数就是每一类种长度为一的个数，如（2）√，（2 4）×

Summary：

·burnside是一种计数方法，用来计算含有不等价类的数量
·burnside算法的关键是找好“置换群”，要做到不重不漏，考虑充分。
·存在的问题：置换是作用在所有方案上的，如果颜色数上升，方案数也与之递增，这种情况下Burnside引理就有些力不能及了。
小例题：POJ2154

---

Polya定理

利用Burnside引理要首先列出所有n^m种可能的染色方案，然后找出在每个置换下保持不变的方案数。显然当m或n很大的时候，这个方法会非常繁琐。
✪我们希望找到其它的方法来计算c1(ak)。
那就是Polya定理
polya定理适用于染色问题方案数问题。
我们设用m种元素涂N中的元素，则不同的方案数M表示为：

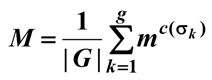
还是上面的例子：

Θ不动：a1=(1)(2)(3)(4)
Θ旋转90度 ：a2=(1 2 3 4)
Θ旋转180度 ：a3=(1 3)(2 4)
Θ旋转270度：a4=(1 4 3 2)

可以看到Burnside引理和Polya定理在某些方面是处处调和的。只不过Polya定理是Burnside的引理的优化罢了。
例题：
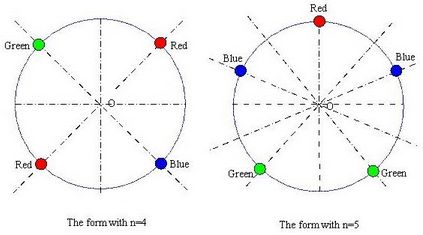
POJ1286 Necklace of Beads —题目链接

Description

Beads of red, blue or green colors are connected together into a circular necklace of n beads ( n < 24 ). If the repetitions that are produced by rotation around the center of the circular necklace or reflection to the axis of symmetry are all neglected, how many different forms of the necklace are there?

Input

The input has several lines, and each line contains the input data n.
-1 denotes the end of the input file.

Output

The output should contain the output data: Number of different forms, in each line correspondent to the input data.

Sample Input

4
5
-1

Sample Output

21
39
Picture：

旋转

当n = 4时，可顺时针旋转0、1、2、3格
0格：（1）（2）（3）（4）互相转化
1格：（1,2,3,4）互相转化
2格：（1,3）（2,4）互相转化
3格：（1,2,3,4）互相转化
So,answer = (1/4) * (3^4+3^1+3^2+3^1)=24
旋转：顺时针旋转i格的置换中，循环的个数为gcd（i，n），每个循环的长度为n/gcd(i,n)
当n=5时，answer = (1/5) * (3^5+3^1*4)=51
以此类推。

对称

当n = 4时，有4条对称轴
其中2条，（1,2）（3,4）互相变化
另2条，（1）（3）（2,4）互相
answer= (1/4) * (2*3^2+2*3^3)=18
当n = 5时，有5条对称轴
每一条，（1）（2,5）（3,4）
answer=(1/5) * (5*3^3)=27
以此类推。
最终answer=（旋转+对称）/ 2。
Code：

#include
#include
typedef long long ll;
ll n,ans;
ll pow(ll x,ll y)
{
    ll ans=1;
    while(y)
    {
        if(y&1)
        {
            ans=(ans*x);;
        }
        y/=2;
        x*=x;
    }
    return ans;
}
ll gcd(ll x,ll y)
{
    return y ? gcd(y, x%y) : x;
}
int main()
{
    while(~scanf("%lld",&n),n!=-1)
    {
        if(n==0)
        {
            puts("0");
            continue;   
        }
        ans=0;
        if(n&1)
        {
            ans+=pow(3,n/2+1)*n;
        }
        else
        {
            ans+=pow(3,n/2+1)*(n/2)+pow(3,n/2)*(n/2);
        }
        for(int i=1;i<=n;i++)
        {
            ans+=pow(3,gcd(i,n));
        }
        printf("%lld\n",ans/(2*n));
    }
    return 0;
}

一般解题思路：

• 寻找“置换”——旋转、翻转等
• 寻找每种置换下的等价状态
• 应用Polya定理直接计数

---

Thanks for reading.