Unity Shader:雾的数学运算以及在Unity中使用Fog
文章目录
- 1,Unity Fog效果图
- 2,uniform fog均匀雾的数学公式推导
- 3,Fog在Unity中的应用
- 4,Unity Fog的源码分析
- 5,Unity exp fog VS uniform fog
1,Unity Fog效果图

Forward,MSAA,Bloom,Global Fog/Exponential Squared/Density 0

Forward,MSAA,Bloom,Global Fog/Exponential Squared/Density 0.045

Forward,MSAA,Bloom,Global Fog/Exponential Squared/Density 0.085

Forward,MSAA,Bloom,Global Fog/Exponential Squared/Density 0.125
2,uniform fog均匀雾的数学公式推导
雾中存在着雾粒子,当光线接近雾粒子时,有一定几率被雾粒子吸收并被散射至其他方向,在此过程中光的初始颜色将会递减,并向雾粒子的颜色递增,这种大面积的颜色变化最终产生了雾中朦胧的效果。
左侧光线的原始颜色称为Color-Enter, Center,右侧最终变化后的颜色称为Color-leave,Cleave。每当Center接触一个雾粒子时,它的颜色发生如下变化:
C l e a v e = C e n t e r − C r e d u c t i o n + C i n c r e a s e Cleave=Center-Creduction+Cincrease Cleave=Center−Creduction+Cincrease
由上图可知:
C r e d u c t i o n = C e n t e r ∗ x % , C i n c r e a s e = C f o g ( 雾 的 颜 色 ) ∗ x % Creduction=Center * x\%, Cincrease=Cfog(雾的颜色) * x\% Creduction=Center∗x%,Cincrease=Cfog(雾的颜色)∗x%
所以
C l e a v e = C e n t e r − ( C e n t e r ∗ x % ) + ( C f o g ∗ x % ) Cleave=Center-(Center * x\%)+(Cfog * x\%) Cleave=Center−(Center∗x%)+(Cfog∗x%)
设h=0~1,表示一个光颜色向雾颜色变化的百分比强度
C l e a v e = ( 1 − h ) ∗ C e n t e r + h ∗ C f o g Cleave=(1-h)*Center+h*Cfog Cleave=(1−h)∗Center+h∗Cfog
改写1-h为g
公 式 1 : C l e a v e = g ∗ C e n t e r + ( 1 − g ) ∗ C f o g 公式1:Cleave=g*Center+(1-g)*Cfog 公式1:Cleave=g∗Center+(1−g)∗Cfog
假设每个雾粒子是等距的,既是每次散色的Creduction和Cincrease都是相等的,那么当发生多次散射时:

例如上图光通过雾粒子发生两次散色,那么:
Cleave=(Center-Creduction+Cincrease)-Creduction+Cincrease
由之前公式可总结出:…-Creduction+Cincrease=…*g+(1-g)*Cfog
因此公式可变为:
C l e a v e = ( C e n t e r ∗ g + ( 1 − g ) ∗ C f o g ) ∗ g + ( 1 − g ) ∗ C f o g Cleave=(Center*g+(1-g)*Cfog)*g+(1-g)*Cfog Cleave=(Center∗g+(1−g)∗Cfog)∗g+(1−g)∗Cfog
= C e n t e r ∗ g 2 + g ( 1 − g ) ∗ C f o g + ( 1 − g ) ∗ C f o g =Center*g^2+g(1-g)*Cfog+(1-g)*Cfog =Center∗g2+g(1−g)∗Cfog+(1−g)∗Cfog
= C e n t e r ∗ g 2 + ( g − g 2 + 1 − g ) ∗ C f o g =Center*g^2+(g-g^2+1-g)*Cfog =Center∗g2+(g−g2+1−g)∗Cfog
= C e n t e r ∗ g 2 + ( 1 − g 2 ) ∗ C f o g =Center*g^2+(1-g^2)*Cfog =Center∗g2+(1−g2)∗Cfog
由此可归纳为一个多次散色的公式,Z作为发生散色的次数,由于前提是每个雾粒子是等距的,所以它也代表距离:
C l e a v e = C e n t e r ∗ g Z + ( 1 − g Z ) ∗ C f o g Cleave=Center*g^Z+(1-g^Z)*Cfog Cleave=Center∗gZ+(1−gZ)∗Cfog
如果将Cleave理解为最终可视颜色也既是Ceye,Center为物体本身颜色既是Cobject,那么:
C e y e = C o b j e c t ∗ g Z + ( 1 − g Z ) ∗ C f o g Ceye=Cobject*g^Z+(1-g^Z)*Cfog Ceye=Cobject∗gZ+(1−gZ)∗Cfog
这里有一个 g Z g^Z gZ的问题。虽然int整数的乘方运算可以用左移实现,但是不适用于浮点数。乘方运算会对GPU造成巨大性能瓶颈。
规避乘方运算,可以利用一个幂函数可以用指数函数重写的性质:
a b = x l o g x a ∗ b a^b=x^{log_x^{a}*b} ab=xlogxa∗b //(引用 2)
因此
g z = 2 l o g 2 g ∗ z g^z=2^{log_2^{g}*z} gz=2log2g∗z //将x取2以发挥GPU可快速实现log2()和exp2()的性能优势
重写后的公式:
C e y e = C o b j e c t ∗ 2 l o g 2 g ∗ z + ( 1 − 2 l o g 2 g ∗ z ) ∗ C f o g Ceye=Cobject*2^{log_2^{g}*z}+(1-2^{log_2^{g}*z})*Cfog Ceye=Cobject∗2log2g∗z+(1−2log2g∗z)∗Cfog
对 2 l o g 2 g 2^{log_2^{g}} 2log2g取反:
公 式 2 : C e y e = C o b j e c t ∗ 2 − ( − l o g 2 g ∗ z ) + ( 1 − 2 − ( − l o g 2 g ∗ z ) ) ∗ C f o g 公式2:Ceye=Cobject*2^{-(-log_2^{g}*z)}+(1-2^{-(-log_2^{g}*z)})*Cfog 公式2:Ceye=Cobject∗2−(−log2g∗z)+(1−2−(−log2g∗z))∗Cfog
此即为模拟‘均匀雾’的最终公式, 2 − ( − l o g 2 g ∗ z ) 2^{-(-log_2^{g}*z)} 2−(−log2g∗z)称为雾的因子f, − l o g 2 g -log_2^{g} −log2g称为雾的浓度d,z称为雾的距离z。d取反后保证了公式的正确逻辑,既当d增加时f将会衰减,也既是Center的乘数衰减,Cfog的乘数增加,浓度d变大,雾的散色增大。
公 式 3 : C e y e = C o b j e c t ∗ f + ( 1 − f ) ∗ C f o g 公式3:Ceye=Cobject*f+(1-f)*Cfog 公式3:Ceye=Cobject∗f+(1−f)∗Cfog
3,Fog在Unity中的应用
在一个有雾的环境中,一个无限远的天空是无法被看见的,既是 f = 2 ( − d ∗ ∞ ) = 0 f=2^{(-d*\infty)}=0 f=2(−d∗∞)=0,因此正常的天空盒在有雾的场景中并不适用。可以用几个plane包围住场景,配合Unity的Global Fog充当天空盒的角色,相比修改Camera的Clear Flag,包围场景的物体在Shader内可以调用Unity Fog函数做到整个场景同步。

plane的材质用default即可,如有特殊需要也可使用其他,注意shader要使用UNITY_TRANSFER_FOG和UNITY_APPLY_FOG函数。
如果使用实时光照的平行光,将平行光颜色改为雾颜色。
进入windows/lighting/settings,找到Other Settings,勾选“Fog”,Mode有Linear,Exponential,Exponential Squared。
Camera的Rendering Path选为forward。
4,Unity Fog的源码分析
一个默认的Unlit Shader
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
UNITY_TRANSFER_FOG(o,o.vertex);
return o;
}
UNITY_TRANSFER_FOG函数定义在UnityCG.cginc的第962行(Unity5.6.5)
#if (SHADER_TARGET < 30) || defined(SHADER_API_MOBILE)
// mobile or SM2.0: calculate fog factor per-vertex
#define UNITY_TRANSFER_FOG(o,outpos) UNITY_CALC_FOG_FACTOR((outpos).z); o.fogCoord.x = unityFogFactor
#else
// SM3.0 and PC/console: calculate fog distance per-vertex, and fog factor per-pixel
#define UNITY_TRANSFER_FOG(o,outpos) o.fogCoord.x = (outpos).z
#endif
可以看出UNITY_TRANSFER_FOG会赋值顶点着色器输出对象o一个fogCoord,有一个唯一成员x,在低配模式下被赋值为计算好的unityFogFactor,高配模式下为o.vertex.z。回到Shader进入片段着色器
fixed4 frag (v2f i) : SV_Target
{
// sample the texture
fixed4 col = tex2D(_MainTex, i.uv);
// apply fog
UNITY_APPLY_FOG(i.fogCoord, col);
return col;
}
Shader调用的UNITY_APPLY_FOG,函数原型在UnityCG.cginc的第989行(Unity5.6.5)
#ifdef UNITY_PASS_FORWARDADD
#define UNITY_APPLY_FOG(coord,col) UNITY_APPLY_FOG_COLOR(coord,col,fixed4(0,0,0,0))
#else
#define UNITY_APPLY_FOG(coord,col) UNITY_APPLY_FOG_COLOR(coord,col,unity_FogColor)
#endif
UNITY_APPLY_FOG(coord,col)被重新定义为UNITY_APPLY_FOG_COLOR(coord,col,unity_FogColor),在FORWARDADD光照模式下,unity_FogColor被改为了黑色。coord为上面已经算好的unityFogFactor(低配)或当前像素的z值(高配),col为当前像素颜色,unity_FogColor应该就是Editor配置Fog时选择的颜色。UNITY_APPLY_FOG_COLOR在978行又被重新定义
#if (SHADER_TARGET < 30) || defined(SHADER_API_MOBILE)
// mobile or SM2.0: fog factor was already calculated per-vertex, so just lerp the color
#define UNITY_APPLY_FOG_COLOR(coord,col,fogCol) UNITY_FOG_LERP_COLOR(col,fogCol,(coord).x)
#else
// SM3.0 and PC/console: calculate fog factor and lerp fog color
#define UNITY_APPLY_FOG_COLOR(coord,col,fogCol) UNITY_CALC_FOG_FACTOR((coord).x); UNITY_FOG_LERP_COLOR(col,fogCol,unityFogFactor)
#endif
在高配模式下,会用参数coord.x(当前像素z值)调用UNITY_CALC_FOG_FACTOR计算雾因子,既是上文均匀雾数学模型中的f。如果是低配模式,在顶点着色器调用UNITY_TRANSFER_FOG函数时就已经计算好了雾因子,节省了片段着色器中的计算,但精度差一点
#define UNITY_CALC_FOG_FACTOR(coord) UNITY_CALC_FOG_FACTOR_RAW(UNITY_Z_0_FAR_FROM_CLIPSPACE(coord))
UNITY_CALC_FOG_FACTOR_RAW先是调用上面根据D3D或OpenGL重定义的UNITY_Z_0_FAR_FROM_CLIPSPACE函数确保z值的正确性,这里不贴代码了。然后是雾因子的计算
#if defined(FOG_LINEAR)
// factor = (end-z)/(end-start) = z * (-1/(end-start)) + (end/(end-start))
#define UNITY_CALC_FOG_FACTOR_RAW(coord) float unityFogFactor = (coord) * unity_FogParams.z + unity_FogParams.w
#elif defined(FOG_EXP)
// factor = exp(-density*z)
#define UNITY_CALC_FOG_FACTOR_RAW(coord) float unityFogFactor = unity_FogParams.y * (coord); unityFogFactor = exp2(-unityFogFactor)
#elif defined(FOG_EXP2)
// factor = exp(-(density*z)^2)
#define UNITY_CALC_FOG_FACTOR_RAW(coord) float unityFogFactor = unity_FogParams.x * (coord); unityFogFactor = exp2(-unityFogFactor*unityFogFactor)
#else
#define UNITY_CALC_FOG_FACTOR_RAW(coord) float unityFogFactor = 0.0
#endif
这里根据Editor Fog设置的选项有三个分支,分别是 l i n e a r , e x p , e x p 2 linear,exp,exp^2 linear,exp,exp2模式。看中间的exp模式。注释写着 factor = exp(-density*z),density是Editor选择的0-1雾浓度重新计算后传到了unity_FogParams.y,coord为像素的z值,移到exp2()函数内展开为 2 ( − u n i t y F o g P a r a m s . y ∗ ( c o o r d ) ) 2^{(-unity_FogParams.y * (coord))} 2(−unityFogParams.y∗(coord)),与上文中均匀雾因子 2 − ( − l o g 2 g ∗ z ) 2^{-(-log_2^{g}*z)} 2−(−log2g∗z)相似,再看一下unity_FogParams.y,在UnityShaderVariables.cginc中有定义
CBUFFER_START(UnityFog)
fixed4 unity_FogColor;
// x = density / sqrt(ln(2)), useful for Exp2 mode
// y = density / ln(2), useful for Exp mode
// z = -1/(end-start), useful for Linear mode
// w = end/(end-start), useful for Linear mode
float4 unity_FogParams;
CBUFFER_END
看注释也不确定exp和exp2是什么模型,跟网上的Exponential fog也不太一样。
计算好了雾因子f,再调用UNITY_FOG_LERP_COLOR对当前像素颜色与雾颜色根据f进行一个lerp线性混合,既是上文中的公式3, C e y e = C o b j e c t ∗ f + ( 1 − f ) ∗ C f o g Ceye=Cobject*f+(1-f)*Cfog Ceye=Cobject∗f+(1−f)∗Cfog
#if (SHADER_TARGET < 30) || defined(SHADER_API_MOBILE)
// mobile or SM2.0: fog factor was already calculated per-vertex, so just lerp the color
#define UNITY_APPLY_FOG_COLOR(coord,col,fogCol) UNITY_FOG_LERP_COLOR(col,fogCol,(coord).x)
#else
// SM3.0 and PC/console: calculate fog factor and lerp fog color
#define UNITY_APPLY_FOG_COLOR(coord,col,fogCol) UNITY_CALC_FOG_FACTOR((coord).x); UNITY_FOG_LERP_COLOR(col,fogCol,unityFogFactor)
#endif
5,Unity exp fog VS uniform fog
最后再分析一下Unity源码中的exp模式。根据注释,y= density / ln(2) = density / 0.6931471806。已知density范围为0-1,所以y的范围为0-1.442695041,设z值为10,对比一下均匀雾和exp模式下的雾因子的值的范围:
Unity exp fog: f = 2 ( − d e n s i t y / l n ( 2 ) ∗ z ) f=2^{(-density / ln(2) * z)} f=2(−density/ln(2)∗z)
density=0
f = 1 f=1 f=1
density=1
f = 2 ( − 1.442695041 ∗ 10 ) = 4.539992973 ∗ 1 0 − 5 f=2^{(-1.442695041 * 10)}=4.539992973*10^{-5} f=2(−1.442695041∗10)=4.539992973∗10−5
均匀雾: f = 2 − ( − l o g 2 g ∗ z ) f=2^{-(-log_2^{g}*z)} f=2−(−log2g∗z)
density=0,g=1-0=1
f = 1 f=1 f=1
density=1,g=1-1=0
f = 2 − ( − l o g 2 0 + ϵ ∗ 10 ) = 无 限 接 近 于 0 f=2^{-(-log_2^{0+\epsilon}*10)}=无限接近于0 f=2−(−log20+ϵ∗10)=无限接近于0
单从取值范围来看,在density接近0的区域均匀雾的模型精度高一点。
设z=5,将雾浓度x与颜色y(像素颜色等于0,雾颜色等于1)化为一个二维坐标系,蓝色为Unity exp公式的曲线,黑色为均匀雾的曲线。反应的是在同一距离,两种模式调整雾浓度对像素颜色的影响:

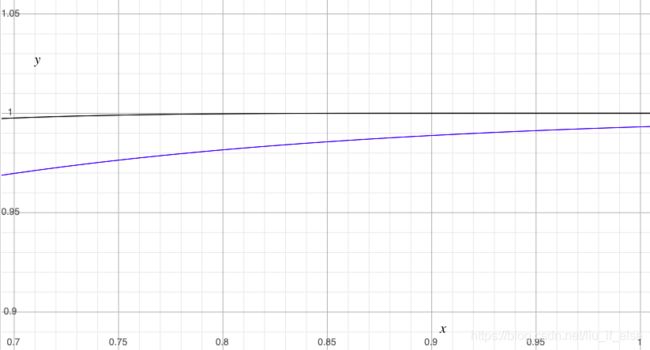
放大density接近1的区域。
再设density=0.4,将z化为x与颜色变为y,图像显示的是两个模式在同一浓度下随着距离增加,像素颜色的变化:
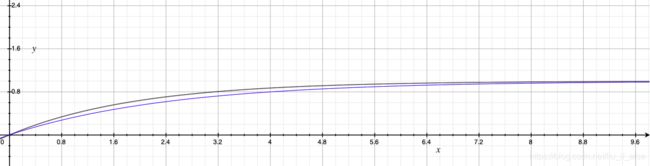
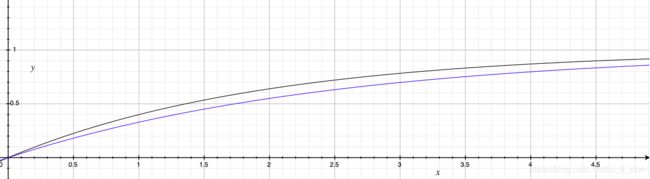
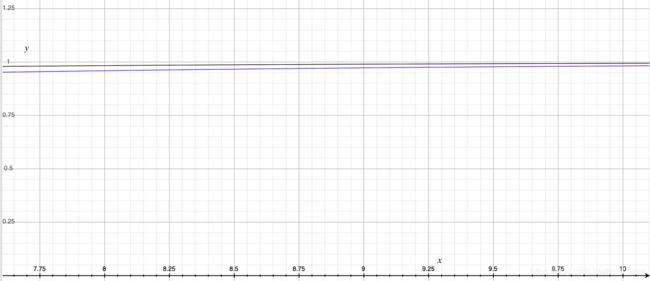
两种模式数值上表现略有差异,但基本变化趋势相同。
引用:
1,Cg Tutorial-Nvidia
2,Production Rendering: Design and Implementation-9.6 Fast Power, Log2 and Exp2 functions
https://books.google.com/books?id=BCC5aTR34C4C&pg=PA270#v=onepage&q&f=false
————————————————————————————
维护日志:
2017-8-22:更改了标题
2017-9-22:在文章起始处增加了4张效果图
2020-2-27:修改错误,增加了Unity源码分析与数值分析



