第五周周赛——你好,你的优先队列到了,请查收题解(出自poj1862,HDU4546,codeforces 277A,437A,638A,523D)
A题:
A题题目链接
题目描述:
Stripies
You are to write a program that will help them to answer this question. You may assume that 3 or more stipies never collide together.
3 72 30 50
120.000
给定N个菌种,每个菌种的质量分别是m1,m2,m3...mN,然后每两个菌种碰撞之后,这两个菌种会融合产生一个新的菌种,新的菌种的质量是2*sqrt(a*b),a,b分别是这两个菌种的质量,保证不会有三个及三个以上的菌种融合在一起,然后问的是最后这N个菌种两两融合后,剩下一个菌种时,最后这个菌种的质量最少可以是多少?保留三位小数。
解析:
拿到这种问题,肯定会涉及到谁先融合谁后融合的问题,那么要怎么安排融合的先后顺序才能使得最后N个菌种融合成的一个菌种的质量最少?很明显,我们先考虑少数的情况,然后再得出一般结论。
考虑有a,b,c三个菌种,那么我们将其中的任意将其中的两个融合,然后再将融合后的菌种再与第三个菌种融合,那么最后所得的菌种的质量为:
2*sqrt(2*sqrt(a*b)*c);
不考虑常数,那么最后最后所得的菌种的质量与sqrt(2*sqrt(a*b)*c)表达式的大小有关,那么将该表达式取平方,得2*sqrt(a*b)*c,然后再取平方,得
4*a*b*c^2,那么我们要使这个表达式最小,很明显,我们可以得出这三者中c一定要是质量最小的菌种。那么从这里可以简单归纳出一般规律,每次取
两个最大的融合,直至剩下一个菌种。(当然也可以用数学归纳法证明)
所以我们为了方便,可以使用优先队列求解,每次取出两个质量最大的融合,(当然也可以直接暴力求解,由于N值范围不大)然后将融合后的结果
加入队列中,直至最后只剩下一个菌种,再输出即可。
完整代码实现:
#include
#include
#include
#include
#include
#include
#include B题题目链接
题目描述:
Home Numbers
The main street of Berland is a straight line with n houses built along it (n is an even number). The houses are located at both sides of the street. The houses with odd numbers are at one side of the street and are numbered from 1 to n - 1 in the order from the beginning of the street to the end (in the picture: from left to right). The houses with even numbers are at the other side of the street and are numbered from 2 to n in the order from the end of the street to its beginning (in the picture: from right to left). The corresponding houses with even and odd numbers are strictly opposite each other, that is, house 1 is opposite house n, house 3 is opposite house n - 2, house 5 is opposite house n - 4 and so on.
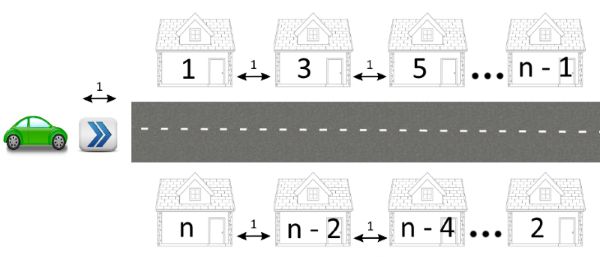
Vasya needs to get to house number a as quickly as possible. He starts driving from the beginning of the street and drives his car to house a. To get from the beginning of the street to houses number 1 and n, he spends exactly 1 second. He also spends exactly one second to drive the distance between two neighbouring houses. Vasya can park at any side of the road, so the distance between the beginning of the street at the houses that stand opposite one another should be considered the same.
Your task is: find the minimum time Vasya needs to reach house a.
The first line of the input contains two integers, n and a (1 ≤ a ≤ n ≤ 100 000) — the number of houses on the street and the number of the house that Vasya needs to reach, correspondingly. It is guaranteed that number n is even.
Print a single integer — the minimum time Vasya needs to get from the beginning of the street to house a.
4 2
2
8 5
3
In the first sample there are only four houses on the street, two houses at each side. House 2 will be the last at Vasya's right.
The second sample corresponds to picture with n = 8. House 5 is the one before last at Vasya's left.
给定一个数n,然后两排的数字呈如下方式排列:
1 3 5 7 ... n-3 n-1
n n-2 n-4 n-6 ... 4 2
然后再给定一个数a,表示要到达的数,每个时间单位车子能够驶过两个对立的房子,不管该数是在左边还是右边时间都是一样的,一开始的时候车子是在这些数的外面。
解析:
具体情况在题意中已经说得很清楚了,解释一下样例1:
给定的数是4,那么两旁排列的则是:
1 3
4 2
那么要到的数字2,则需要两个时间单位。即(n-a)/2+1,到达奇数时则是(a+1)/2.
那么这道题只要简单的分奇偶情况就能解决了。
完整代码实现:
#include
int main(){
int n,a;
while(scanf("%d %d",&n,&a)==2&&n&&a){
if(a%2!=0){
printf("%d\n",(a+1)/2);
}
else{
printf("%d\n",(n-a)/2+1);
}
}
return 0;
}
C题:
C题题目链接
题目描述:
T^T学长考四级
大家都知道,咱们的T^T学长要毕业了,可是,他有一个很大的遗憾,一个是大学期间没泡到妹子(真是个悲伤的故事),另外一个呢,就是英语四级老是考不过。所以呢,我们的T^T学长就决定在毕业之前一定要把四级过了去。
可是,他很懒,信誓旦旦的说着要过四级,但是还是裸考了。。。(肯定又过不了)
我们都知道,英语四级的选择题都是4个选项的。
所以,在考四级之前,他想到了一个主意,偷偷告诉你他的主意:
-
如果其中有一个选项比其他每个选项的一半短,或者其中有一个选项比其他每个选项的两倍长,那么T^T学长就觉得这个选项很不错。
-
如果T^T学长只发现其中一个选项很不错的话,那么他就会选择这个选项;否则的话,他也就没办法了,也就只能选C了。
现在,给你一个含有四个选项的选择题,你能预测一下T^T学长会选哪个吗?
The first line starts with "A." (without quotes), then followed the description of choice A. The next three lines contains the descriptions of the other choices in the same format. They are given in order: B, C, D. Please note, that the description goes after prefix "X.", so the prefix mustn't be counted in description's length.
Each description is non-empty and consists of at most 100 characters. Each character can be either uppercase English letter or lowercase English letter, or "_".
Print a single line with the child's choice: "A", "B", "C" or "D" (without quotes).
A.VFleaKing_is_the_author_of_this_problem
B.Picks_is_the_author_of_this_problem
C.Picking_is_the_author_of_this_problem
D.Ftiasch_is_cute
D
A.ab
B.abcde
C.ab
D.abc
C
A.c
B.cc
C.c
D.c
B
In the first sample, the first choice has length 39, the second one has length 35, the third one has length 37, and the last one has length 15. The choice D (length 15) is twice shorter than all other choices', so it is great choice. There is no other great choices so the child will choose D.
In the second sample, no choice is great, so the child will choose the luckiest choice C.
In the third sample, the choice B (length 2) is twice longer than all other choices', so it is great choice. There is no other great choices so the child will choose B.
考虑两种情况即可,如果其中一个选项比其余三个选项的两倍都要短,那么他肯定比第二小的选项的两倍都要短,同样的如果其中
一个选项比其余三个选项的两倍都要长,那么它肯定要比第二大的选项的两倍都要长,两者满足其一方可输出,否则的话输出C。
完整代码实现:
#include
#include
#include
#include
#include
#include
#include D题:
D题题目链接
题目描述:
T^T的ACM
最近,T^T出了一些ACM编程题,决定在我大工院举行一场公开赛。
假设题目的数量一共是n道,这些题目的难度被评级为一个不超过1000的非负整数,并且一场比赛至少需要一个题,而这场比赛的难度,就是所有题目的难度之和,同时,我们认为一场比赛与本场题目的顺序无关,而且题目也不会重复。
显而易见,很容易得到如下信息:
假设比赛只用1个题目,有n种方案;
假设比赛使用2个题目,有(n-1)*n/2种方案;
假设比赛使用3个题目,有(n-2)*(n-1)*n/6种方案;
............
假设比赛使用全部的n个题目,此时方案只有1种。
经过简单估算,T^T发现总方案数几乎是一个天文数字!
为了简化问题,现在T^T只想知道在所有的方案里面第m小的方案,它的比赛难度是多少呢?
2 5 6 1 1 1 1 1 5 25 1 2 3 4 5
Case #1: 2 Case #2: 11
D题题解传送门(来自亲爱的荣钦学长):
【优先队列】-HDU4546比赛难度
E题:
E题题目链接
题目描述:
Statistics of Recompressing Videos
A social network for dogs called DH (DogHouse) has k special servers to recompress uploaded videos of cute cats. After each video is uploaded, it should be recompressed on one (any) of the servers, and only after that it can be saved in the social network.
We know that each server takes one second to recompress a one minute fragment. Thus, any server takes m seconds to recompress a m minute video.
We know the time when each of the n videos were uploaded to the network (in seconds starting from the moment all servers started working). All videos appear at different moments of time and they are recompressed in the order they appear. If some video appeared at time s, then its recompressing can start at that very moment, immediately. Some videos can await recompressing when all the servers are busy. In this case, as soon as a server is available, it immediately starts recompressing another video. The videos that await recompressing go in a queue. If by the moment the videos started being recompressed some servers are available, then any of them starts recompressing the video.
For each video find the moment it stops being recompressed.
The first line of the input contains integers n and k (1 ≤ n, k ≤ 5·105) — the number of videos and servers, respectively.
Next n lines contain the descriptions of the videos as pairs of integers si, mi (1 ≤ si, mi ≤ 109), where si is the time in seconds when the i-th video appeared and mi is its duration in minutes. It is guaranteed that all the si's are distinct and the videos are given in the chronological order of upload, that is in the order of increasing si.
Print n numbers e1, e2, ..., en, where ei is the time in seconds after the servers start working, when the i-th video will be recompressed.
3 2
1 5
2 5
3 5
6
7
11
6 1
1 1000000000
2 1000000000
3 1000000000
4 1000000000
5 1000000000
6 3
1000000001
2000000001
3000000001
4000000001
5000000001
5000000004
题意:
这道题题意很难懂,英语鸡肋+_+,问了荣钦学长之后,了解到这题类似于银行柜台办理业务排队。
给定n个人,k个窗口
下面n行给出每个人到银行的时间和每个人办理手续需要的时间。
输出每个人离开的时间
先到的人先服务,意思就是说这n行中,在前面的人是先到的。
解析:
这道题我们可以用优先队列模拟一下办理手续的过程,一开始我们标记这k个窗口,然后就是每个人开始办理业务,
一开始的时候,每个窗口都是空的,所以前面来的人是不用等待的,而后,当人越来越多的时候,就要开始排队了,那么每次每个窗口办理结束后会有一个时间点,如果这个时间点大于下一个来办理手续的人到银行的时间,那么他在这个时间点就可以直接办理手续,那么他离开的时间点就是该时间点 + 该人办理手续需要的时间;而如果他在这个时间点的时候还没有来的话,那么这个柜台就暂时空着了,直到他来了,那么他离开的时间点就是他到达的时间点 + 该人办理手续需要的时间。
因此,我们要怎么样模拟这个过程呢?我们可以试着拿样例1来分析一下:
3 2
1 5
2 5
3 5
总共有3个人,2个柜台,那么第一个人来的时候,开始在第一个柜台办理业务,当在第二分钟的时候,第二个人来了,那么他就到
第二个柜台去办理业务了,当在第三分钟的时候,第三个人来了,可是第一第二个人都还没走,所以他就要开始等待了,等到第六
分钟的时候,第一个人走了,然后第三个人接着到第一个柜台办理业务,直到办理结束。
所以呢,一开始我们标记这k个窗口,然后每次柜台满的时候,后面在等待的人都是接着到最快办理完手续的柜台那边,
因此这道题我们可以用优先队列模拟一下办理手续的过程,k个窗口,每个窗口都用0标记,表示当前窗口是空的,这样的话,前面的
k个人都是一来就可以直接办理业务了。然后就是每个人开始办理业务,每次将取出的时候,
取最小的值(即最快办完的那个人的时间点),然后办理完了之后,将自己办理结束的时间点再压入队列中,
直到所有的人都办理结束。
完整代码实现:
#include
#include
#include
#include
#include
#include
#include F题:
F题题目链接
题目描述:
Learning Languages
The "BerCorp" company has got n employees. These employees can use m approved official languages for the formal correspondence. The languages are numbered with integers from 1 to m. For each employee we have the list of languages, which he knows. This list could be empty, i. e. an employee may know no official languages. But the employees are willing to learn any number of official languages, as long as the company pays their lessons. A study course in one language for one employee costs 1 berdollar.
Find the minimum sum of money the company needs to spend so as any employee could correspond to any other one (their correspondence can be indirect, i. e. other employees can help out translating).
The first line contains two integers n and m (2 ≤ n, m ≤ 100) — the number of employees and the number of languages.
Then n lines follow — each employee's language list. At the beginning of the i-th line is integer ki (0 ≤ ki ≤ m) — the number of languages the i-th employee knows. Next, the i-th line contains ki integers — aij (1 ≤ aij ≤ m) — the identifiers of languages the i-th employee knows. It is guaranteed that all the identifiers in one list are distinct. Note that an employee may know zero languages.
The numbers in the lines are separated by single spaces.
Print a single integer — the minimum amount of money to pay so that in the end every employee could write a letter to every other one (other employees can help out translating).
5 5
1 2
2 2 3
2 3 4
2 4 5
1 5
0
8 7
0
3 1 2 3
1 1
2 5 4
2 6 7
1 3
2 7 4
1 1
2
2 2
1 2
0
1
In the second sample the employee 1 can learn language 2, and employee 8 can learn language 4.
In the third sample employee 2 must learn language 2.
题意:
第一行给定n个人和m种语言(序号分别是1-m),然后接下来是每个人懂的语言数量以及语言的序号,每一行开头的第一个数是该
人懂的语言数量x,然后接下来x个数,表示他懂的这x种语言的序号。注意:允许有人一门语言都不懂,这样的话该行就为0,然后
这n个人需要互相交流(可以不直接交流,意思就是可以请人翻译他说的话,但是这两个交流的人懂的语言中必须要有一门相同
的,这样的话两个人才能够互相交流),由于每个人懂的语言数量和类别都不一定是相同的,所以必然有无法交流的情况,那么就
要去培训,每位员工培训一门语言需要花费1元,问至少花费多少钱,才能够使得员工之间能够互相交流?
解析:
在考虑特殊情况之前,我们可以自己先举一点数据较小的例子,试着分析一下,看看自己是否能够灵光一现O(∩_∩)O~
比如说这样的一个例子:
4 6
2 1 2
2 2 3
2 4 5
2 5 6
以上的例子即是说有4名员工,总共有6种语言,而后的四行则是这四名员工分别懂的语言数量及类别。
那么我们看,员工1和员工2懂的语言中有同一门语言,员工3和员工4也有懂同一门语言,因此他们之间两两是可以相互交流的。
但是员工1和员工3呢?他们俩要怎么交流?
假若是员工1用语言1发邮件给员工3,但是员工3不懂这门语言,并且也没有一个人懂这门语言,因此用语言1员工3是看不懂的。
同样的,就算是员工1用语言2发邮件给员工3,虽然有员工2懂这门语言,员工3可以叫员工2帮忙翻译一下,可是员工2懂的语言只有2和3,他要帮助
员工3翻译的话也只能翻译成语言2或者语言3,无论是翻译成哪种语言,员工3都是看不懂的。所以呢,这时候就发现了员工之间无法交流的情况,那
么就要有员工去学习新的语言才行,那么前面我们知道:
员工1和员工2懂的语言中有同一门语言,员工3和员工4也有懂同一门语言,因此他们之间两两是可以相互交流的。
所以呢,我们可以让员工1或者员工2去学一门在员工3和员工4之间能够流通的语言(即不是只有一个人懂的语言),当然也可以学习其他的员工3和员
工4懂的语言,这样的话交流起来比较麻烦,需要间接地通过几个人翻译,才能够翻译成自己懂的语言。(具体可以自己分析看看,比如说员工1去学
语言4,那么怎么样实现员工2和员工4之间的交流呢?开动脑筋自己画一画O(∩_∩)O~~)那么可以让员工1去学语言5,这
样的话员工3或者员工4要和员工1或者员工2交流,只要用语言5交流即可,然后每个圈子里的人还可以找人帮忙翻译成自己懂的语言。
有了上面的描述,我们可以将其抽象成一些特殊的情况,比如说:
员工1,2,3能够两两交流(两两交流在这里的含义就是说这个圈子里的人能够互相直接交流,或者能够叫圈子里面的人帮忙翻译,总的就是说圈子里
的这些人,要交流起来是没有障碍的)
同样的假设员工4,5也能够两两交流,员工6,7,8也能够两两交流
那么要怎么样才能使得员工1—8都能够两两交流呢?
这时候问题就来了,我们暂且标记这三个能够两两交流的圈子为m1,m2,m3。
然后每个圈子里的人都商讨着,该怎么样和其他圈子里的人交流呢?
这时候m1里面的小机灵说:“要是我们三个圈子都有一门相同的语言大家不就可以交流了。”
于是小机灵便叫m1圈子里的老大去和其他两个圈子的老大商量,后面敲定了,m1,m2圈子里的老大一起学m3中流通的一门语言,
然后圈子之间交流的时候,小的们就叫老大帮忙翻译(当老大可真不容易),这样的话,三个圈子里的人要交流的话,用m3中流通
的语言就好了,于是就实现了员工1—8的两两交流。
那么问题来了?要怎么确定你跟我是一个圈子的人呢?
比如说:
我懂的语言是1,2
你是2,3
他是1
我们三个人就是有话说,♪(^∇^*),然后就融合到一个圈子里了。
言归正传,从上面的分析,很明显得出,这是一道考察并查集的题目。先将能够两两交流的人融合到一个圈子里,然后最后判断总
共有多少个圈子(连通分量),而有些人是一门语言都不懂,那么他们也要跟着学,所以最后的答案便是圈子数目 - 1 + 一门语言都
不懂的人数(有一个圈子的老大不用学,另外所有圈子的老大和一门语言都不懂的人学这个圈子的流通语言,便可以实现两两交
流) 注意特判:所有的人都是一门语言都不懂的时候,那么每个人学一门相同的语言即可,这时候的答案便是总人数。
完整代码实现:
/**由于数据比较小,因此可以优化*/
#include
int father[210],n,m,k,v[210],f[210],ans;
void Init(){
for(int i = 1;i <= m;++i){
father[i] = i;
}
}
int find_set(int node){
if(father[node]!=node){
father[node] = find_set(father[node]);
}
return father[node];
}
void solve(){
scanf("%d %d",&n,&m);
Init();
for(int i = 1;i <= n;++i){
scanf("%d",&k);
if(!k){
++ans;
}
for(int i = 1;i <= k;++i){
scanf("%d",&f[i]);
++v[f[i]];
}
for(int i = 1;i < k;++i){
father[find_set(f[i])] = find_set(f[i+1]);
}
}
bool tmp = false;
for(int i = 1;i <= m;++i){
if(father[i]==i&&v[i]){
++ans;
tmp = true;
}
}
printf("%d\n",tmp ? ans - 1 : n);
}
int main(){
solve();
return 0;
}
如有错误,还请指正,O(∩_∩)O谢谢