数据结构与算法C++之图的遍历（深度优先遍历）

图的遍历：深度优先遍历

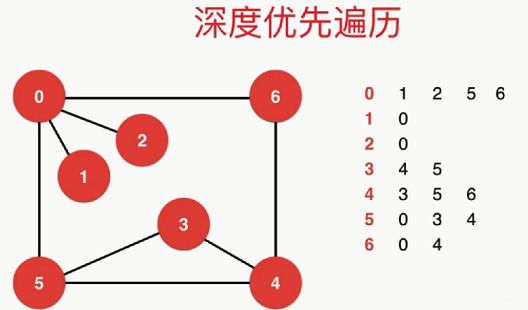
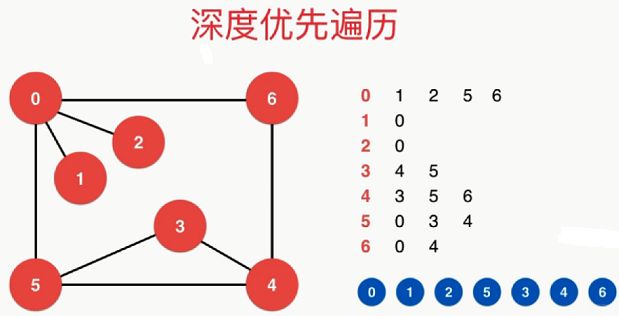
（1）首先遍历节点0，与0连接的节点有1,2,5,6，那么先遍历节点1，下面再看与节点1相连的是节点0，节点0已经遍历过了，那么继续遍历节点2，与2连接的节点是0，节点0已经遍历过了，那么开始遍历节点5，

（2）与5连接的节点有0,3,4，节点0已经遍历过了，那么开始遍历节点3，3没有被遍历过，记录下3，与节点3连接的节点是4和5，首先4没有被遍历过，记录下4，继续查看与4连接的节点3,5,6，前两个节点3和5都遍历过了，只有节点6没有被遍历过，把6记录下来，

（3）与节点6连接的有节点0和4，这两个都遍历过了，那么就退回到节点4，与节点4连接的三个节点都遍历过了，就继续退回到节点3，查看节点5，节点5已经遍历过了，而且与5连接的0,3,4已经遍历过了，退回到节点0，继续查看节点6，与6连接的节点0和4都遍历过了，遍历结束

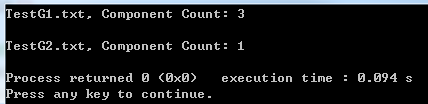
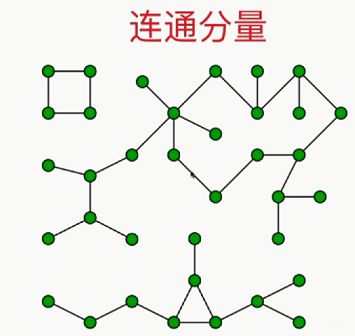
使用图遍历可以求连通分量，如下图，一共有3个连通分量

下面是程序实现

#include 
#include 
#include 
#include "SparseGraph.h"
#include "DenseGraph.h"
#include "ReadGraph.h"
#include "Component.h"

using namespace std;

int main()
{
    string filename1 = "testG1.txt";
    SparseGraph g1( 13, false );
    ReadGraph<SparseGraph> readGraph1( g1, filename1 );
    Component<SparseGraph> component1( g1 );
    cout<<"TestG1.txt, Component Count: "<<component1.count()<<endl;

    cout<<endl;

    string filename2 = "testG2.txt";
    DenseGraph g2( 7, false );
    ReadGraph<DenseGraph> readGraph2( g2, filename2 );
    Component<DenseGraph> component2( g2 );
    cout<<"TestG2.txt, Component Count: "<<component2.count()<<endl;

    return 0;
}

深度优先遍历Component.h定义为

#include 
#include 
using namespace std;


template <typename Graph>
class Component{

private:
    Graph &G;
    bool *visited;
    int ccount;
    int *id;

    void dfs(int v){
        visited[v] = true;
        id[v] = ccount;
        typename Graph::adjIterator adj(G, v);
        for ( int i = adj.begin(); !adj.end(); i = adj.next() ){
            if ( !visited[i] )
                dfs(i);
        }
    }

public:
    Component(Graph &graph):G(graph){
        visited = new bool[G.V()];
        id = new int[G.V()];
        ccount = 0;
        for (int i = 0; i < G.V(); i++){
            visited[i] = false;
            id[i] = -1;
        }

        for (int i = 0; i < G.V(); i++)
            if (!visited[i]){
                dfs(i);
                ccount ++;
            }
    }

    ~Component(){
        delete[] visited;
        delete[] id;
    }

    int count(){
        return ccount;
    }

    bool isConnected( int v, int w){
        assert( v >= 0 && v < G.V() );
        assert( w >= 0 && w < G.V() );
        return id[v] == id[w];
    }
};

"SparseGraph.h"定义为

#include 
#include 
#include 

using namespace std;

//稀疏图 - 邻接表
class SparseGraph{

private:
    int n, m;
    bool directed;
    vector< vector<int> > g;

public:
    SparseGraph( int n, bool directed ){
        this->n = n;
        this->m = 0;
        this->directed = false;
        for ( int i = 0; i < n; i++ ){
            g.push_back(vector<int>());
        }
    }

    ~SparseGraph() {

    }

    int V(){return n;}
    int E(){return m;}

    void addEdge(int v, int w){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );

        g[v].push_back(w);
        if ( v != w && !directed )
            g[w].push_back(v);

        m++;
    }

    bool hasEdge(int v, int w){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
        for (int i = 0; i < g[v].size(); i++){
            if ( g[v][i] == w )
                return true;
        }
        return false;
    }

    void show(){

        for(int i = 0; i < n; i ++){
            cout<<"vertex "<<i<<":\t";
            for( int j = 0; j < g[i].size(); j++ )
                cout<<g[i][j]<<"\t";
            cout<<endl;
        }
    }

    class adjIterator{
    private:
        SparseGraph &G;
        int v;
        int index;
    public:
        adjIterator(SparseGraph &graph, int v): G(graph){
            this->v = v;
            this->index = 0;
        }

        int begin(){
            index = 0;
            if (G.g[v].size())
                return G.g[v][index];
            return -1;
        }

        int next(){
            index++;
            if (index < G.g[v].size())
                return G.g[v][index];
            return -1;
        }
        bool end(){
            return index >= G.g[v].size();
        }
    };
};

"DenseGraph.h"定义为

#include 
#include 
#include 

// ³íÃÜͼ - ÁÚ½Ó¾ØÕó
class DenseGraph {

private:
    int n;
    int m;
    bool directed;
    vector< vector<bool> > g;

public:
    DenseGraph( int n, bool directed ){
        this->n = n;
        this->m = 0;
        this->directed = directed;
        for (int i = 0; i < n; i++){
            g.push_back( vector<bool>(n,false) );
        }
    }
    ~DenseGraph() {

    }

    int V(){return n;}
    int E(){return m;}

    void addEdge(int v, int w ){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );

        if ( hasEdge(v, w) )
            return;
        g[v][w] = true;
        if ( !directed )
            g[w][v] = true;

        m++;
    }

    bool hasEdge(int v, int w){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
        return g[v][w];
    }

    void show(){
        for( int i = 0; i < n; i ++ ){
            for( int j = 0; j < n; j ++)
                cout<<g[i][j]<<"\t";
            cout<<endl;
        }
    }

    class adjIterator{
    private:
        DenseGraph &G;
        int v;
        int index;
    public:
        adjIterator(DenseGraph &graph, int v): G(graph){
            this->v = v;
            this->index = -1;
        }

        int begin(){
            index = -1;
            return next();
        }

        int next(){
            for (index += 1; index < G.V(); index++){
                if ( G.g[v][index] )
                    return index;
            }
            return -1;
        }
        bool end(){
            return index >= G.V();
        }
    };
};

"ReadGraph.h"定义为

#include 
#include 
#include 
#include 
#include 

using namespace std;

template<typename Graph>
class ReadGraph{

public:
    ReadGraph(Graph &graph, const string &filename){
        ifstream file(filename.c_str());
        string line;
        int V,E;

        assert( file.is_open() );

        assert( getline(file, line) );
        stringstream ss(line);
        ss>>V>>E;

        assert( V == graph.V() );

        for(int i = 0; i < E; i++){
            assert( getline(file, line) );
            stringstream ss(line);

            int a, b;
            ss>>a>>b;
            assert( a >= 0 && a < V);
            assert( b >= 0 && b < V);
            graph.addEdge( a, b );
        }
    }
};

testG1.txt
第一行第一个13表示有13个节点，第二个13表示13条边
第二行到最后一行是13条边

13 13
0 5
4 3
0 1
9 12
6 4
5 4
0 2
11 12
9 10
0 6
7 8
9 11
5 3

testG2.txt
第一行第一个13表示有13个节点，第二个13表示13条边
第二行到最后一行是13条边

7 8
0 1
0 2
0 5
0 6
3 4
3 5
4 5 
4 6

输出为

可以看出第一张图有3个连通分量，第二张图有1个连通分量