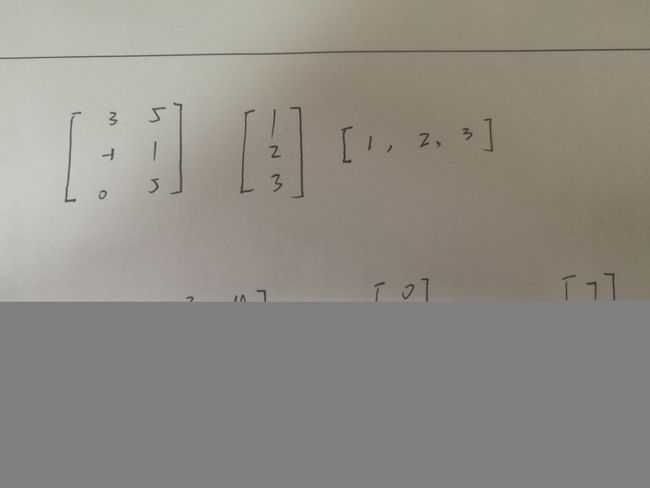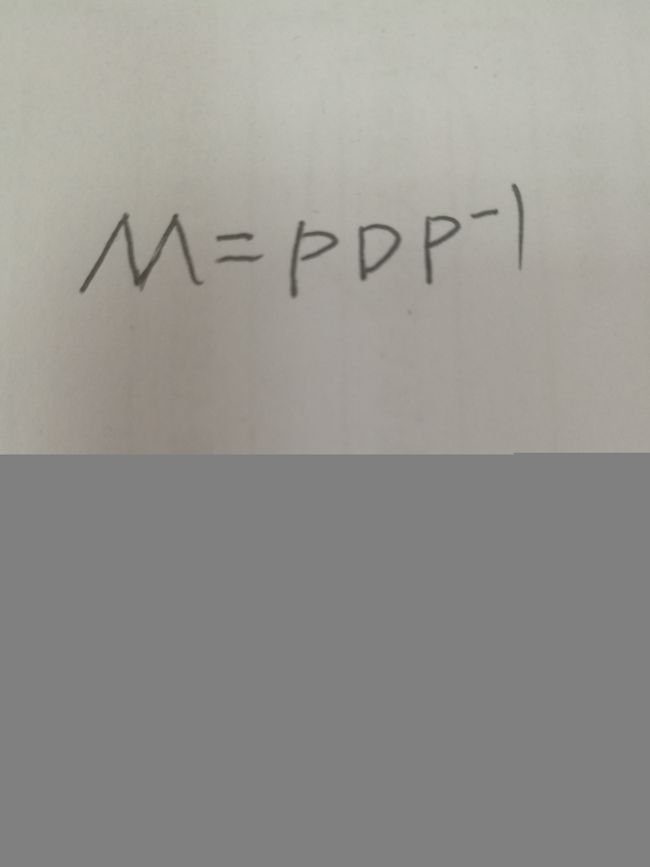python矩阵计算（特征值，特征向量，对角化）

用sympy进行矩阵计算的基本操作

首先创建矩阵基本操作，首先构造下图中的矩阵，特别注意：一维矩阵的建立格式。

from sympy import *
import math 
import numpy as np
a = Matrix([[3,5],[-1,1],[0,5]])
print(a)

b = Matrix([1,2,3])#三行一列
print(b.shape)


c = Matrix([[1,2,3]])
print(c.shape)

x = Matrix([[1,3,4],[4,2,1]])
y = Matrix([0,1,1])
print(x*y)#两行一列

运行结果 

Matrix([[3, 5], [-1, 1], [0, 5]])
(3, 1)
(1, 3)
Matrix([[7], [3]])

列和行的操作

列和行的操作，M.row(0)将的到第一行,M.col(-1)会得到最后一列

M = Matrix([[1,3,2],[5,6,3]])
print(M.shape)#打印矩阵的维度
"""列和行的操作，M.row(0)将的到第一行,M.col(-1)会得到最后一列"""
print("打印第一行")
print(M.row(0))
print("打印最后一列")
print(M.col(-1))

(2, 3)
打印第一行
Matrix([[1, 3, 2]])
打印最后一列
Matrix([[2], [3]])

删除和插入数据操作 

M = Matrix([[1,3,2],[5,6,3]])
print(M.shape)#打印矩阵的维度
"""删除矩阵的行或列，用 row_del和col_del"""
M.col_del(0)
print(M)

M.row_del(1)
print(M)

print("给矩阵添加行或列，用 row_del和col_del")
print(M)
M = M.row_insert(1,Matrix([[0,4]]))#添加行
print("在第二行添加数据")
print(M)
M = M.col_insert(0,Matrix([1,-2]))
print("在第一列添加数据")
print(M)

(2, 3)
Matrix([[3, 2], [6, 3]])
Matrix([[3, 2]])
给矩阵添加行或列，用 row_del和col_del
Matrix([[3, 2]])
在第二行添加数据
Matrix([[3, 2], [0, 4]])
在第一列添加数据
Matrix([[1, 3, 2], [-2, 0, 4]])

基本数学运算

M = Matrix([[1,3],[5,3]])
N = Matrix([[4,3],[8,1]])
print("矩阵相加")
print(M+N)
print("矩阵相乘")
print(M*N)
print("矩阵的平方")
print(M**2)
print("矩阵乘以一个数")
print(M*3)
print("求矩阵的逆")
print(M**-1)
print("矩阵的转置")
print(M.T)

矩阵相加
Matrix([[5, 6], [13, 4]])
矩阵相乘
Matrix([[28, 6], [44, 18]])
矩阵的平方
Matrix([[16, 12], [20, 24]])
矩阵乘以一个数
Matrix([[3, 9], [15, 9]])
求矩阵的逆
Matrix([[-1/4, 1/4], [5/12, -1/12]])
矩阵的转置
Matrix([[1, 5], [3, 3]])

矩阵的高级操作

M = Matrix([[1,3,4],[5,0,3],[3,5,7]])
print(M)
print("计算矩阵的行列式")
print(M.det())
print("化简矩阵,返回两个元素，第一个是矩阵，第二个是元组")
print(M.rref())

Matrix([[1, 3, 4], [5, 0, 3], [3, 5, 7]])
计算矩阵的行列式
7
化简矩阵
(Matrix([
[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]), [0, 1, 2])

特征值、特征向量和对角化

特征值

M = Matrix([[3,-2,4,-2],[5,3,-3,-2],[5,-2,2,-2],[5,-2,-3,3]])
print(M)
print("计算矩阵的特征值")
print(M.eigenvals())

Matrix([[3, -2, 4, -2], [5, 3, -3, -2], [5, -2, 2, -2], [5, -2, -3, 3]])
计算矩阵的特征值
{3: 1, -2: 1, 5: 2}，M的特征值为-2,3,5，特征值-2,3具有代数多重性1，特征值5具有代数多重性2.

特征向量

M = Matrix([[3,-2,4,-2],[5,3,-3,-2],[5,-2,2,-2],[5,-2,-3,3]])

print("计算矩阵的特征向量")
print(M.eigenvects())

计算矩阵的特征向量
[(-2, 1, [Matrix([[0],[1],[1],[1]])]),

(3, 1, [Matrix([[1],[1],[1],[1]])]),

(5, 2, [Matrix([[1],[1],[1],[0]]), Matrix([[ 0],[-1],[ 0],[ 1]])])]，

对角化

M = Matrix([[3,-2,4,-2],[5,3,-3,-2],[5,-2,2,-2],[5,-2,-3,3]])

print("计算矩阵的对角化矩阵")
P,D = M.diagonalize()
print(P)
print(D)

计算矩阵的对角化矩阵
Matrix([[0, 1, 1, 0], [1, 1, 1, -1], [1, 1, 1, 0], [1, 1, 0, 1]])
Matrix([[-2, 0, 0, 0], [0, 3, 0, 0], [0, 0, 5, 0], [0, 0, 0, 5]])