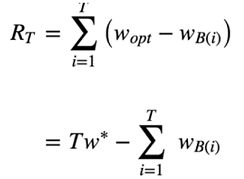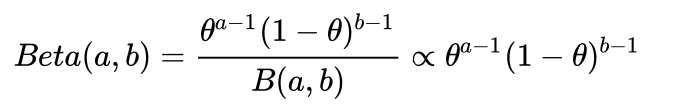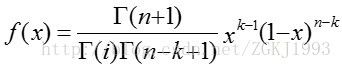Multi-Armed bandit --------强化学习（含ucb python 代码）

　前言：阅尽千章泪成江，看了Ｎ人写的博客,感觉很多人为让人看不懂而写的，我写的目的就是为了简单了解，入门很不深

１.什么是多臂老虎机？

   一个赌徒，要去摇老虎机，走进赌场一看，一排老虎机，外表一模一样，但是每个老虎机吐钱的概率可不一样，他不知道每个老虎机吐钱的概率分布是什么，那么每次该选择哪个老虎机可以做到最大化收益呢？这就是多臂赌博机问题（Multi-armed bandit problem, K-armed bandit problem, MAB）。

思考一下，每个老虎机赢钱的期望和方差是不同的（抽象成别的问题的话，可能概率分布也是不同的），我们可以根据已知的数据，用最大似然估计的方法估算出期望，做出选择选择期望最大的

２．基础知识

　　１．ｒｅｇｒｅｔ（累计遗憾）

　　　作用：　对于算法评估标准之一

Wopt 是最佳reward(收益)，Wb(i)是做出选择的收益

　　　２．Ｂｅｔａ分布

用ｇａｍｍａ函数表示如下

 

　第一个公式中的ａ是第二公式中的ｉ，ｂ是第二个公式的　ｎ－ｋ

　！！！！！！！beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它根据成功失败的次数可以给出了所有概率出现的可能性大小，Ｂeta(成功次数，失败)。

详情：https://www.zhihu.com/question/30269898

３．用到的算法

　　　１．朴素Bandit算法

　　　　最朴素的Bandit算法就是：先随机试若干次，计算每个臂的平均收益，一直选均值最大那个臂。这个算法是人类在实际中最常采用的，不可否认，它还是比随机乱猜要好。

　　　２．ϵ−greedy 策略

　　　　两种操作，explore与exploit，exploit选择当前value最大的arm尝试，explore随机选择一个arm尝试。

　　　　这个方法就是设定一个ε值, 用来指导到底是Explore 还是 Exploit。比如将ε设定为0.1，以保证将10%的次数投入在探索（Explore）,90%的次数用于利用(Exploit)。

　　　　具体操作就是，每次玩的时候就抽一个0到1的随机数，如果这个数大于ε，则玩你认为中奖概率（预估中奖概率）最大的那个拉杆。如果小于ε，则随机再选择一个拉杆，得到收益后，更新这个拉杆的预估中奖概率，以便于下次选择做参考。

　　　　通过尝试调整每一个arm对应的估计成功概率（value）。在每次尝试完成后，均根据中奖结果更新对应arm的value。更新value的策略如下：

 

其中，a表示尝试（action），Qk(a) 表示尝试的估计成功率（value），k表示该尝试被试过的次数，Rk(a) 表示该次尝试的结果（reward）。

　　　　３ UCB算法（Upper Confidence Bound）

　　　　我们发现上面两个方法中，某个拉杆预估的中奖概率是随着这个拉杆被拉动的次数而变化的。我们是通过预估概率作为评判标准，来决定去拉哪一个拉杆。

如果一个拉杆没有被拉到，那么这个拉杆的预估中奖概率就不会改变。然而通过直觉就可以理解，一个拉杆的预估概率的准确度是跟你总共拉了多少次拉杆（所有的拉杆被拉的次数）相关的，拉得越多预估概率就越准确。这个时候我们引入UCB概率，而不是预估概率来作为选择拉杆的评判标准。

这里涉及到的理论知识叫做Chernoff-Hoeffding bound理论。大意就是，真实概率与预估概率的差距是随着实验（拉杆）的次数成指数型下降的。

　　初始化：先对每一个臂都试一遍；

　　按照如下公式计算每个臂的分数，然后选择分数最大的臂作为选择：

观察选择结果，更新t和Tjt。其中加号前面是这个臂到目前的收益均值，后面的叫做bonus，本质上是均值的标准差，t是目前的试验次数，Tjt是这个臂被试次数。

这个公式反映一个特点：均值越大，标准差越小，被选中的概率会越来越大，同时哪些被选次数较少的臂也会得到试验机会。

 

#!/usr/bin/python
# coding:utf-8 
# 19-3-25 上午9:48
# @File    : ucb1.py
import math


def find_index(x):
    return x.index(max(x))


class UCB1():
    def __init__(self, counts, values):
        self.counts = counts
        self.values = values
        return

# unfault triplet arm bandit

    def __init__(self):
        self.counts = [0, 0, 0]
        self.values = [0, 0, 0]

    def initialize(self, n_arms):
        self.counts = [0 for col in range(n_arms)]
        self.values = [0 for col in range(n_arms)]

    def select_arm(self):
        n_arms = len(self.counts)
# select unchosen arm every once
        for arm in range(n_arms):
            if self.counts[arm] == 0:
                return arm
        ucb_value = [0.0 for arm in range(n_arms)]
        total_counts = sum(self.counts)

        for arm in range(n_arms):
            bonus = math.sqrt((2*math.log(total_counts))/float(self.counts))
            ucb_value[arm] = self.values[arm] + bonus
            return find_index(ucb_value)

    def update(self, chosen_arm, reward):
        self.counts[chosen_arm] = self.counts[chosen_arm] + 1
        n = self.counts[chosen_arm]
        value = self.values[chosen_arm]
        # normalization
        new_value = ((n-1)/float(n)) * value + (1/float(n)) * reward
        self.values[chosen_arm] = new_value
        return

　　４Thompson sampling算法

　　简单介绍一下它的原理，要点如下：

1. 假设每个臂是否产生收益，其背后有一个概率分布，产生收益的概率为p。
2. 我们不断地试验，去估计出一个置信度较高的“概率p的概率分布”就能近似解决这个问题了。
3. 怎么能估计“概率p的概率分布”呢？ 答案是假设概率p的概率分布符合beta(wins, lose)分布，它有两个参数: wins, lose。
4. 每个臂都维护一个beta分布的参数。每次试验后，选中一个臂，摇一下，有收益则该臂的wins增加1，否则该臂的lose增加1。
5. 每次选择臂的方式是：用每个臂现有的beta分布产生一个随机数b，选择所有臂产生的随机数中最大的那个臂去摇。