算法导论-动态规划

动态规划算法

动态规划（dynamic programming）是通过组合子问题来求解原问题的方法，它应用于解决子问题重叠的情况，即不同子问题具有公共的子问题。
通常动态规划可以按照如下四个步骤进行设计：
1.刻画一个最优解的结构特征；
2.递归地定义最优解的值；
3.计算最优解的值，通常采用自底向上的方法；
4.利用计算出的信息构造一个最优解（按照要求，可有可无）。

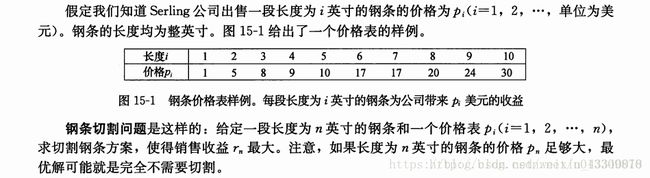
一、钢条切割问题

自顶向下递归实现

CUT-ROD(p,n)
if n==0
	return 0
q=-∞
for i=1 to n
	q=max(q,p[i]+CUT-ROD(p,n-i))
return q

用Python实现代码：

def value_max(p, n):
    if n == 0:
        return 0
    q = 0
    for i in range(0, n):
        q = max(q, p[i] + value_max(p, n - i - 1))
    return q

price= [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
print (value_max(price, 8))

对于长度为n的钢条，CUT-ROD显然考察了所有2^(n-1)种可能的切割方案。朴素递归算法之所以效率很低，是因为它反复求解相同的子问题。
动态规划方法是付出额外的内存空间来节省计算时间，是典型的时空权衡的例子。而时间上的节省可能是非常巨大的：可能将一份指数时间的解转化为一个多项式时间的解。
动态规划有两种等价的实现方法
第一种是带备忘录的自顶向下法：

MEMOIZED-CUT-ROD(p,n)
let r[0..n]be a new array
for i=0 to n
r[i]=-∞
return MEMOIZED-CUT-ROD-AUX(p,n,r)

MEMOIZED-CUT-ROD-AUX(p,n,r)
if r[n]>=0
return r[n]
if n==0
	q=0
else q=-∞
	for i=i to n
		q=max(q,p[i]+MEMOIZED-CUT-ROD-AUX(p,n-i,r))
		r[n]=q
		return q

用Python写得代码为：

def cutMemo(p,n):
    r=[0]*(n+1)
    def value_max(p,n,r):
        if n==0:
            return 0
        q=0
        for i in range(0,n):
            q=max(q,p[i]+value_max(p,n-i-1,r))
            r[i]=q
        print (r)
        return q
    return value_max(p,n,r)
price=[1,5,8,9,10,17,17,20,24,30]
print (cutMemo(price,8))

第二种是自底向上法：

BOTTOM-UP-CUT-ROD(p,n)
let r[0..n] be a new array
r[0]=0
for j=1 to n
	q=-∞
	for i=1 to j
		q=max(q,p[i]+r[j-i])
   r[j]=q
 return r[n]

用Python编写的代码如下：

def cutMemo(p,n):
    r=[0]*(n+1)
    for i in range(1,n+1):
        if n==0:
            return 0
        q=0
        for j in range(1,i+1):
            q=max(q,p[j-1]+r[i-j])
            r[i]=q
    return r
price=[1,5,8,9,10,17,17,20,24,30]
print (cutMemo(price,8))

子问题图

它是一个有向图，每个定点唯一地对应一个子问题。若求子问题x的最优解时需要直接用到子问题y的最优解，那么在子问题图中就会有一条子问题x的顶点到子问题y的顶点的有向边。我们可以将子问题图看做自顶向下递归调用树的“简化版”或“收缩版”，因为书中所对应相同子问题的结点合并为图中的单一顶点，相关的所有边都从父结点指向子节点。
子问题图G=（V，E）的规模可以帮助我们确定动态规划算法的运行时间。由于每个子问题只求解一次，因此算法运行时间内等于每个子问题求解时间之和。

二、矩阵链乘法

我们称有如下性质的矩阵乘积链为完全括号化的：它是一个单一矩阵，或者是两个完全括号化的矩阵乘积链的积，且已外加括号。
两个矩阵相乘的标准算法的伪代码：

MATRIX-MULTIPLY(A,B)
if A.columns≠B.rows
	error "incompatible dimensions"
else let C be a new A.rows*B.columns matrix
	for i=1 to A.rows
		for j=1 to B.columns
		Cij=0
		for k=1 to A.columns
			Cij=Cij+Aik*Bkj
return C

两个矩阵A和B只有相容，即A的列数等于B的行数时，才能相乘。
矩阵链乘法问题：给定n个矩阵的链，矩阵Ai的规模为Pi-1*Pi（1<=i<=n），求完全括号花方案，使得计算乘积A1A2…An所需的乘法次数最少。
计算AiAi+1…Aj最小代价括号化方案的递归求解公式为：

对矩阵链AiAi+1…Aj最优括号化的子问题的伪代码为：

MATRIX-CHAIN-ORDER(p)
n=p.length-1
let m[1..n,1..n] and s[1..n-1,2..n] be new tables
for i=1 to n
	m[i,i]=0
for l=2 to n
	for i=1 to n-l+1
		j=i+l-1
		m[i,j]=∞
		for k=i to j-1
			q=m[i,k]+m[k+1,j]+p_(i-1) p_k p_j
			if q

用Python编写代码为：

	def MATRIX_CHAIN_ORDER(p):
    n=len(p)
    s=[[0 for j in range(n)] for i in range(n)]
    m=[[0 for j in range(n)] for i in range(n)]
    for l in range(2,n):
        for i in range(1,n-l+1):
            j=i+l-1
            m[i][j]=1e9
            for k in range(i,j):
                q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]
                if q

动态规划原理

适合应用动态规划办法求解的最优化问题应该具备的两个要素：最优子结构和子问题重叠。
无权最短路径：找到一条从u到v的边数最少的路径。无权最短路径问题具有最优子结构性质。
无权最长路径：找到一条从u到v的边数最多的简单路径。无权最长路径问题不具有最优子结构性质。此问题是NP完全的。
简单路径：路径上的各顶点均不互相重复。
最长简单路径问题的子结构与最短路径差别大的原因是：虽然最长路径问题和最短路径问题的解都用到了两个子问题，但两个最长简单路径子问题是相关的，而两个最短路径子问题是无关的。子问题无关的含义是，同一个原问题的一个子问题的解不影响另一个子问题的解。

三、最长公共子序列

给定一个序列X=（x1,x2…xm）,另一个序列Z=（z1,z2…zk）满足如下条件时称为X的子序列，即存在一个严格递增的X的下标序列（i1，i2,…,ik），对所有j=1,2,…k，满足x_i_j=z_j。

计算最长公共子序列的伪代码：

LCS-LENGTH(X,Y)
m=X.length
n=Y.length
let b[1..m,1..n] and c[0..m,0..n]be new tables
for i=1 to m
	c[i,0]=0
for j=0 to n
	c[0,j]=0
for i=1 to m
	for j=1 to n
		if xi==yi
			c[i,j]=c[i-1,j-1]+1
			b[i,j]="↖"
		elseif c[i-1,j]≥c[i,j-1]
					c[i,j]=c[i-1,j]
					b[i,j]="↑"
		else c[i,j]=c[i,j-1]
				b[i,j]="←"
return c and b

用Python编写的代码：

def LCS_LENGTH(X, Y):
    m= len(X)
    n = len(Y)
    c = [[0 for i in range(n + 1)] for j in range(m + 1)]
    flag = [[0 for i in range(n + 1)] for j in range(m + 1)]
    for i in range(m):
        for j in range(n):
            if X[i] == Y[j]:
                c[i + 1][j + 1] = c[i][j] + 1
                flag[i + 1][j + 1] = 'ok'
            elif c[i + 1][j] > c[i][j + 1]:
                c[i + 1][j + 1] = c[i + 1][j]
                flag[i + 1][j + 1] = 'left'
            else:
                c[i + 1][j + 1] = c[i][j + 1]
                flag[i + 1][j + 1] = 'up'
    return c, flag


def PRINT_LCS(flag, X, i, j):
    if i == 0 or j == 0:
        return
    if flag[i][j] == 'ok':
        PRINT_LCS(flag, X, i - 1, j - 1)
        print(X[i - 1], end='')
    elif flag[i][j] == 'left':
        PRINT_LCS(flag, X, i, j - 1)
    else:
        PRINT_LCS(flag, X, i - 1, j)
X = 'ABCBDAB'
Y = 'BDCABA'
c, flag = LCS_LENGTH(X, Y)
for i in c:
    print(i)
print('')
for j in flag:
    print(j)
print('')
PRINT_LCS(flag, X, len(X), len(Y))
print('')

四、最优二叉搜索树

最优二叉搜索树不一定是高度最矮的树。而且概率最高的关键字也不一定出现在二叉搜索树的根结点。

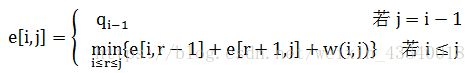
最优二叉搜索树的期望搜索代价为e[i,j],对于包含关键树Ki,…,Kj的子树，所有概率之和为：

求解最优二叉树搜索的伪代码：

OPTIMAL-BST(p,q,n)
let e[1..n+1,0..n],w[1..n+1,0..n],and root[1..n,1..n]be new tables
for i=1 to n+1
	e[i,i-1]=q_i-1
	w[i,i-1]=q_i-1
for l=1 to n
	for i=1 to n-l+1
		j=i+l-1
		e[i,j]=∞
		w[i,j]=w[i,j-1]+p_i+q_j
		for r=i to j
			t=e[i,r-1]+e[r+1,j]+w[i,j]
			if t