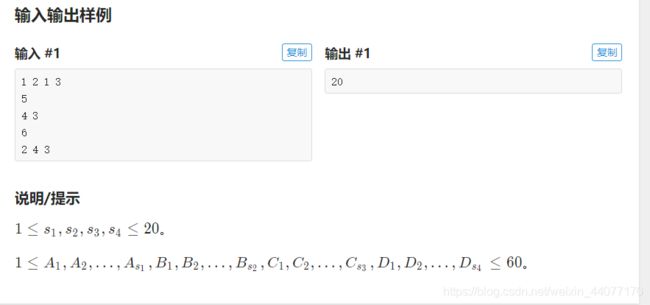
P2392 kkksc03考前临时抱佛脚
这道题咋一看上去就是贪心,用优先队列,每次弹出第一大第二大的元素,然后加上较小的那一个,将两者之差压入优先队列,一直循环到优先队列只有一个元素,加上剩下的那个元素即可。
#include 自信满满的提交上去,竟然只有60分。。。。说实话,我只看得出来是贪心,题目这样例也能达到我自己认为的贪心策略的解,但机智如我,很快发现就是一道DP题,反正贪心我贪不来,可能可以贪心,是我太弱?
dp思路:如果一门功课的总时间为T,那么最好的情况就是T/2的时间学完这门功课,左右脑齐开动。但是也可能达不到T/2,所以我们选择几门功课尽可能到达T/2,此时就抓换为,T/2的背包,最多可以容纳多少价值的物品,此时的物品的重量和价值相当,也就是说学习时长等于物品的重量也等于物品的价值,如果选完后物品总价值为X(这门功课一部分的学习时长),则另一部分学习时长为T-X,此时判断哪一个更大即可。加上大的那个,即这门功课所花费的最少时间。
你也可以自己想办法,使得一部分的学习时长尽可能的靠近T/2,同上面。当然,有了0-1背包问题的基础,这种类似0-1背包问题的题目也是小儿科了,下面是AC代码“
#include 2020-4-3更新一波,这种题目怎么少得了爆搜呢,毕竟暴力出奇迹。
此题的时间很宽裕,也可能是数据太水了,反正最后10个点都过了。
思路:枚举1—s[i]的所有题目,分别加到左脑和右脑,枚举完毕以后选出左右脑最大值中最小的那一个,展开来看就是一颗二叉树了,我们只需要套用一下二叉树的先序遍历即可。AC代码~
#include