计算智能——遗传算法解决TSP问题实验
遗传算法解决TSP问题
- 定义
- 遗传算法
- TSP问题
- 算法流程
- 参数说明
- 代码
- 主程序 main.m
- 染色体的路程代价函数 mylength.m
- 适应度函数 fit.m
- 交叉操作函数 cross.m
- 变异函数 Mutation.m
- 对调函数 exchange.m
- 连点画图函数 plot_route.m
- 实验结果
- N=25 M=100 Pc=0.8 Pmutation=0.05（不同的城市序列）
- N=25 M=100 Pc=0.8 Pmutation=0.05
- N=100 M=100 Pc=0.8 Pmutation=0.05
- N=25 M=200 Pc=0.8 Pmutation=0.05
- N=25 M=100 Pc=0.5 Pmutation=0.05
- N=25 M=100 Pc=0.8 Pmutation=0.09
- 结果分析
- 其他条件相同，城市数量相同城市序列不同
- 其他条件相同，城市数量不同
- 其他条件相同，群体规模不同
- 其他条件相同，交叉概率不同
- 其他条件相同，变异概率不同
- 与蚁群算法区别
定义
遗传算法
遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。
TSP问题
假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
算法流程
参数说明
- M 种群数
影响算法的搜索能力和运行效率。
若N设置较大，一次进化所覆盖的模式较多，可以保证群体的多样性,从而提高算法的搜索能力,但是由于群体中染色体的个数较多，势必增加算法的计算量,降低了算法的运行效率。
若N设置较小,虽然降低了计算量,但是同时降低了每次进化中群体包含更多较好染色体的能力。 - Pc 交叉概率
决定了进化过程种群参加交配的染色体平均数目Pc*N。交叉概率太大的话,就失去意义了,就变成随机算法了；太小的话,收敛太慢.通常的做法是采用自适应的方法。 - Pmutation 变异概率
增加群体进化的多样性,决定了进化过程中群体发生变异的基因平均个数。
Pmutation的值不宜过大。因为变异对已找到的较优解具有一定的破坏作用，如果Pmutation的值太大,可能会导致算法目前所处的较好的搜索状态倒退回原来较差的情况。
代码
主程序 main.m
%main
clear;
clc;
%%%%%%%%%%%%%%%输入参数%%%%%%%%
N=25; %%城市的个数
M=100; %%种群的个数
ITER=2000; %%迭代次数
%C_old=C;
m=2; %%适应值归一化淘汰加速指数
Pc=0.8; %%交叉概率
Pmutation=0.05; %%变异概率
%%生成城市的坐标
% pos=randn(N,2);
rand('state', 0);pos=rand(N,2)*6-3;
%%生成城市之间距离矩阵
D=zeros(N,N);
for i=1:N
for j=i+1:N
dis=(pos(i,1)-pos(j,1)).^2+(pos(i,2)-pos(j,2)).^2;
D(i,j)=dis^(0.5);
D(j,i)=D(i,j);
end
end
%%生成初始群体
popm=zeros(M,N);
for i=1:M
popm(i,:)=randperm(N);%随机排列，比如[2 4 5 6 1 3]
end
%%随机选择一个种群
R=popm(1,:);
figure(1);
scatter(pos(:,1),pos(:,2),'rx');%画出所有城市坐标
axis([-3 3 -3 3]);
figure(2);
plot_route(pos,R); %%画出初始种群对应各城市之间的连线
axis([-3 3 -3 3]);
%%初始化种群及其适应函数
fitness=zeros(M,1);
len=zeros(M,1);
for i=1:M%计算每个染色体对应的总长度
len(i,1)=myLength(D,popm(i,:));
end
maxlen=max(len);%最大回路
minlen=min(len);%最小回路
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);%找到最小值的下标，赋值为rr
R=popm(rr(1,1),:);%提取该染色体，赋值为R
for i=1:N
fprintf('%d ',R(i));%把R顺序打印出来
end
fprintf('\n');
fitness=fitness/sum(fitness);
distance_min=zeros(ITER+1,1); %%各次迭代的最小的种群的路径总长
nn=M;
iter=0;
while iter<=ITER
fprintf('迭代第%d次\n',iter);
%%选择操作
p=fitness./sum(fitness);
q=cumsum(p);%累加
for i=1:(M-1)
len_1(i,1)=myLength(D,popm(i,:));
r=rand;
tmp=find(r<=q);
popm_sel(i,:)=popm(tmp(1),:);
end
[fmax,indmax]=max(fitness);%求当代最佳个体
popm_sel(M,:)=popm(indmax,:);
%%交叉操作
nnper=randperm(M);
% A=popm_sel(nnper(1),:);
% B=popm_sel(nnper(2),:);
%%
for i=1:M*Pc*0.5
A=popm_sel(nnper(i),:);
B=popm_sel(nnper(i+1),:);
[A,B]=cross(A,B);
% popm_sel(nnper(1),:)=A;
% popm_sel(nnper(2),:)=B;
popm_sel(nnper(i),:)=A;
popm_sel(nnper(i+1),:)=B;
end
%%变异操作
for i=1:M
pick=rand;
while pick==0
pick=rand;
end
if pick<=Pmutation
popm_sel(i,:)=Mutation(popm_sel(i,:));
end
end
%%求适应度函数
NN=size(popm_sel,1);
len=zeros(NN,1);
for i=1:NN
len(i,1)=myLength(D,popm_sel(i,:));
end
maxlen=max(len);
minlen=min(len);
distance_min(iter+1,1)=minlen;
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);
fprintf('minlen=%d\n',minlen);
R=popm_sel(rr(1,1),:);
for i=1:N
fprintf('%d ',R(i));
end
fprintf('\n');
popm=[];
popm=popm_sel;
iter=iter+1;
%pause(1);
end
%end of while
figure(3)
plot_route(pos,R);
axis([-3 3 -3 3]);
figure(4)
plot(distance_min);
染色体的路程代价函数 mylength.m
%染色体的路程代价函数 mylength.m
function len=myLength(D,p)%p是一个排列
[N,NN]=size(D);
len=D(p(1,N),p(1,1));
for i=1:(N-1)
len=len+D(p(1,i),p(1,i+1));
end
end
适应度函数 fit.m
%适应度函数fit.m，每次迭代都要计算每个染色体在本种群内部的优先级别，类似归一化参数。越大约好！
function fitness=fit(len,m,maxlen,minlen)
fitness=len;
for i=1:length(len)
fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;
end
交叉操作函数 cross.m
%交叉操作函数 cross.m
function [A,B]=cross(A,B)
L=length(A);
if L<10
W=L;
elseif ((L/10)-floor(L/10))>=rand&&L>10
W=ceil(L/10)+8;
else
W=floor(L/10)+8;
end
%%W为需要交叉的位数
% p=round((rand())*(L-W)+1);
p=unidrnd(L-W+1);%随机产生一个交叉位置
%fprintf('p=%d ',p);%交叉位置
for i=1:W
x=find(A==B(1,p+i-1));
y=find(B==A(1,p+i-1));
[A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1));
[A(1,x),B(1,y)]=exchange(A(1,x),B(1,y));
end
end
变异函数 Mutation.m
%变异函数 Mutation.m
function a=Mutation(A)
index1=0;index2=0;
nnper=randperm(size(A,2));
index1=nnper(1);
index2=nnper(2);
%fprintf('index1=%d ',index1);
%fprintf('index2=%d ',index2);
temp=0;
temp=A(index1);
A(index1)=A(index2);
A(index2)=temp;
a=A;
end
对调函数 exchange.m
%对调函数 exchange.m
function [x,y]=exchange(x,y)
temp=x;
x=y;
y=temp;
end
连点画图函数 plot_route.m
%连点画图函数 plot_route.m
function plot_route(a,R)
scatter(a(:,1),a(:,2),'rx');
hold on;
plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)]);
hold on;
for i=2:length(R)
x0=a(R(i-1),1);
y0=a(R(i-1),2);
x1=a(R(i),1);
y1=a(R(i),2);
xx=[x0,x1];
yy=[y0,y1];
plot(xx,yy);
hold on;
end
end
实验结果
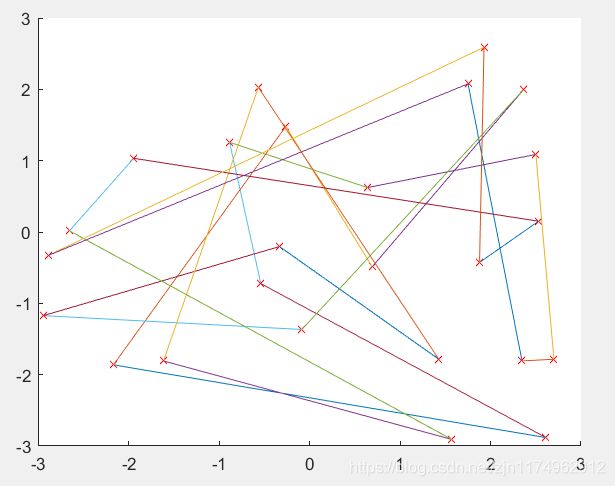
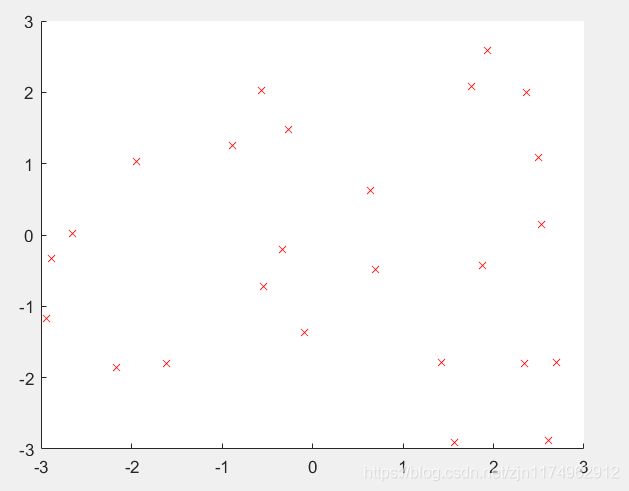
城市分布图1：（N=25）
城市分布图2：（N=25）
城市分布图：（N=100）
本次算法中采用控制变量法，因此除了观察改变城市数量对结果的影响的情况以继相同城市数量不同城市序列对结果的影响的情况外，其他情况下的城市分布图都相同，故先给出城市分布图。
第一张城市数量为25的城市分布图仅对应第一个结果 第二张城市数量为25的城市分布图对应剩下的城市数量为25的结果
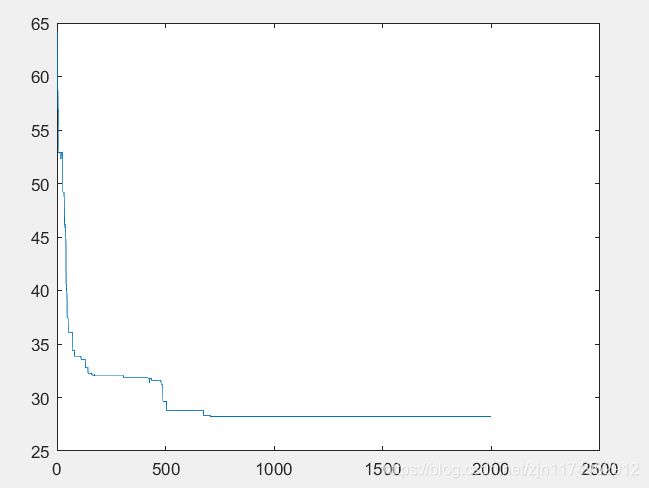
N=25 M=100 Pc=0.8 Pmutation=0.05（不同的城市序列）
2000次迭代后的结果：
迭代第2000次
minlen=2.822505e+01
15 25 1 12 20 23 7 9 19 11 2 24 18 5 4 22 21 16 6 8 10 14 13 3 17
初始路线：
算法执行后：
最短路径下降趋势：
运行时间：
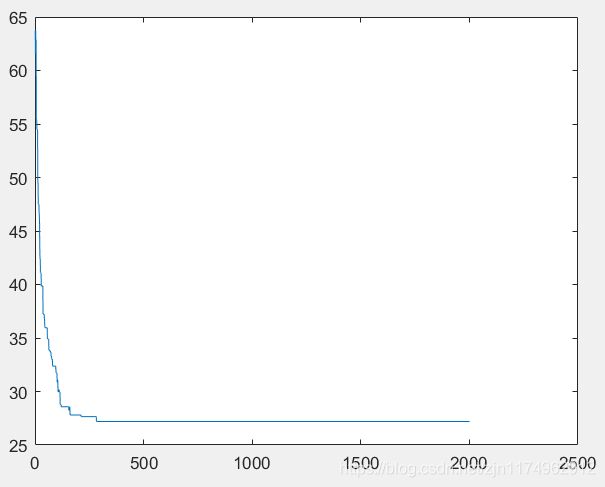
N=25 M=100 Pc=0.8 Pmutation=0.05
2000次迭代后的结果：
迭代第2000次
minlen=2.719610e+01
6 17 1 5 14 2 25 24 8 21 15 22 16 7 11 23 13 18 20 9 12 3 10 19 4
初始路线：
算法执行后：
最短路径下降趋势：
运行时间：
N=100 M=100 Pc=0.8 Pmutation=0.05
2000次迭代后的结果：
迭代第2000次
minlen=1.033575e+02
27 24 55 94 99 85 40 100 34 90 70 77 57 44 87 97 69
95 19 48 61 83 28 43 47 72 15 2 88 53 75 6 5 41 14 23
84 89 76 32 9 81 45 63 59 56 16 50 68 36 33 98 66 71
12 65 37 13 17 1 82 73 86 93 18 62 20 58 52 38 22 51
30 39 67 49 29 10 60 80 79 4 91 31 42 92 21 8 25 7 3
74 11 96 64 46 54 35 78 26
初始路线：
算法执行后：
最短路径下降趋势：
运行时间：
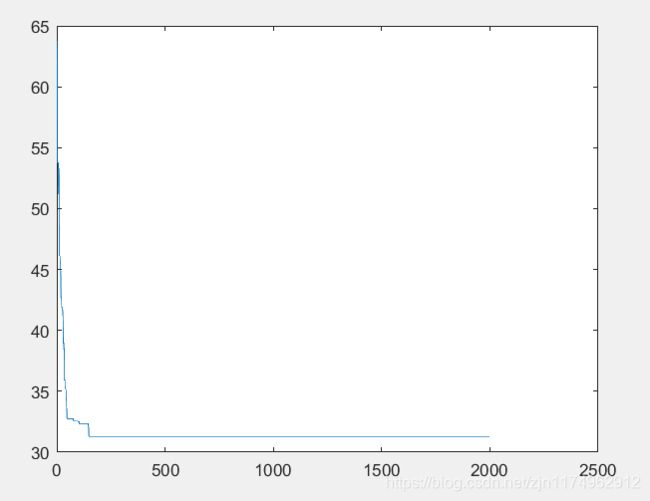
N=25 M=200 Pc=0.8 Pmutation=0.05
2000次迭代后的结果：
迭代第2000次
minlen=3.129641e+01
3 23 13 18 20 9 12 10 8 21 15 16 7 22 24 25 2 19 4 6 17 1 5 14 11
初始路线：
算法执行后：
最短路径下降趋势：
运行时间：
N=25 M=100 Pc=0.5 Pmutation=0.05
2000次迭代后的结果：
迭代第2000次
minlen=3.171891e+01
17 1 5 23 3 7 16 24 8 21 15 22 10 19 25 2 4 11 12 9 20 18 13 14 6
初始路线：
算法执行后：
最短路径下降趋势：
运行时间：
N=25 M=100 Pc=0.8 Pmutation=0.09
2000次迭代后的结果：
迭代第2000次
minlen=2.659864e+01
5 17 6 14 23 11 4 2 25 24 8 21 15 22 16 7 10 19 3 12 9 20 18 13 1
初始路线：
算法执行后：
最短路径下降趋势：
运行时间：
结果分析
其他条件相同，城市数量相同城市序列不同
不同城市序列下TSP算法的结果不同，收敛速度也不同，但是总体的运行时间差不多。
其他条件相同，城市数量不同
对于更多的城市数量，在有限的迭代次数（2000次）中似乎达不到收敛，应该考虑适当增加迭代次数，更多的城市数量下总体的运行时间也更长一点。
其他条件相同，群体规模不同
增加种群数量，总体运行时间增加，算法收敛更快，但搜索出来的最短路径更长，即搜索能力下降了。
其他条件相同，交叉概率不同
减小交叉概率，算法收敛速度大大降低，搜索出来的最短路径也更长，因此可以看出较小的交叉概率搜索能力不强，合适的交叉概率为0.8，但较小的价差概率运行时间更短一点。
其他条件相同，变异概率不同
增大变异概率，搜索出来的最短路径更小了，总的运行时间也更快一点，但收敛的比较慢。
与蚁群算法区别
从以上算法分析和实验结果可见:蚁群优化算法和遗传算法都是一种结合了分布式计算,易于并行实现,同时具有较强鲁棒性的概率搜索仿生算法。蚁群.算法是模拟由简单个体组成的群落与环境以及个体之间的互动行为,即社会系统,从而可能产生不可预测的群体行为,而遗传算法是模拟基因进化的过程。它们在实现TSP问题中的共同点有:
①都容易出现过早收敛,陷入局部最优值。
②算法本身在参数选择与取值上无法在理论上得不到严格的证明,只能通过实验的方法来确定其优化组合。
③对搜索空间两者都没有特殊的要求，如可导性连续性、凹凸性等辅助信息，实用范围更加广泛。
区别在于:蚁群算法是通过信息素的累积和更新而收敛于最优路径,但初期信息素匮乏、导致算法速度慢;而遗传算法虽具有快速全局搜索能力，但对于系统中的反馈信息却没有利用,往往导致无为的冗余迭代，求解效率低。因此,在城市规模大于25时,遗传算法的搜索能力将逐渐下降,大到一定程度时,如想在迭代次数内获得最优解,但时间太长,无法忍受。此时蚁群算法表现好于遗传算法,可在很少的迭代次数内达到最优解。当城市规模过大时,蚊群算法可能出现停滞现象,从而也无法得到最优解。