Algorithm: DP (II): 求Maximum 问题 关键在于每一步的全局最优的选择关于做和不做（做则代表当前local的最优 > 不做的全局最优）

1235. Maximum Profit in Job Scheduling

 

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

 

Example 1:

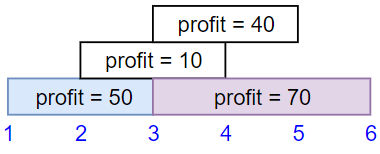
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

 

Constraints:

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
• 1 <= startTime[i] < endTime[i] <= 10^9
• 1 <= profit[i] <= 10^4

class Solution {
    // find maximum, minimum, how many different plans -> likely DP. 
public:
    int jobScheduling(vector& startTime, vector& endTime, vector& profit) {
        for (int i = 0; i <  startTime.size(); ++i) {
            start_time_with_maxprofit_[startTime.at(i)] = 0;
            start_time_with_job_info_[startTime.at(i)].push_back(make_pair(endTime.at(i), profit.at(i)));
        }
        
        auto it_last_optimum = start_time_with_maxprofit_.rbegin();
        for (auto it_start_most_profit = start_time_with_maxprofit_.rbegin(); it_start_most_profit != start_time_with_maxprofit_.rend(); ++it_start_most_profit) {
            int max_possible_profit = 0;
            for (auto it_start_job_info : start_time_with_job_info_.at(it_start_most_profit->first)) {
                // find all possible end time and then the most close possible follow up job max profits
                auto most_close_follow_up = start_time_with_maxprofit_.lower_bound(it_start_job_info.first);
                int local_max_possible_profit = 0;
                if (most_close_follow_up != start_time_with_maxprofit_.end()) {
                    // can do both afterward and now
                    local_max_possible_profit = it_start_job_info.second + most_close_follow_up->second;
                } else {
                    // can only now
                    local_max_possible_profit = it_start_job_info.second;
                }
                if (it_start_most_profit != start_time_with_maxprofit_.rbegin()) {
                    // compare if do or not do
                    // mistake 2: DP is about doing or not doing. Also, 如果现在做而且后面的也可以做，也未必是当前的最优。有可能不做这个任务，还是用原来的前一步最优解是最优。
                    local_max_possible_profit = max(it_last_optimum->second, local_max_possible_profit);
                }
                max_possible_profit = max(max_possible_profit, local_max_possible_profit);
            }
            it_start_most_profit->second = max_possible_profit;
            it_last_optimum = it_start_most_profit;
        }
        
        return (start_time_with_maxprofit_.begin()->second);
    }
    
private:
    map start_time_with_maxprofit_;
    // mistake 1: may have multiple jobs start at a same time
    unordered_map > > start_time_with_job_info_; 
};

826. Most Profit Assigning Work

 

We have jobs: difficulty[i] is the difficulty of the ith job, and profit[i] is the profit of the ith job. 

Now we have some workers. worker[i] is the ability of the ith worker, which means that this worker can only complete a job with difficulty at most worker[i]. 

Every worker can be assigned at most one job, but one job can be completed multiple times.

For example, if 3 people attempt the same job that pays $1, then the total profit will be $3.  If a worker cannot complete any job, his profit is $0.

What is the most profit we can make?

Example 1:

Input: difficulty = [2,4,6,8,10], profit = [10,20,30,40,50], worker = [4,5,6,7]
Output: 100 
Explanation: Workers are assigned jobs of difficulty [4,4,6,6] and they get profit of [20,20,30,30] seperately.

Notes:

• 1 <= difficulty.length = profit.length <= 10000
• 1 <= worker.length <= 10000
• difficulty[i], profit[i], worker[i]  are in range [1, 10^5]

class Solution {
public:
    int maxProfitAssignment(vector& difficulty, vector& profit, vector& worker) {
        int size = difficulty.size();
        map difficulty_to_profit;
        for (int i = 0; i < size; ++i) {
            if (difficulty_to_profit.count(difficulty.at(i)) == 0 
                || difficulty_to_profit.at(difficulty.at(i)) < profit.at(i)) {
                // 错误1：有可能同一难度有不同的profit
                difficulty_to_profit[difficulty.at(i)] = profit.at(i); 
            }
        }
        
        // construct a dp map 
        unordered_map difficulty_to_max_profit;
        auto last_iter = difficulty_to_profit.begin();
        for (auto iter = difficulty_to_profit.begin(); iter != difficulty_to_profit.end(); ++iter) {
          if (iter == difficulty_to_profit.begin()) {
              continue;
          }
          
          if (last_iter->second > iter->second) {
              iter->second = last_iter->second;
          }
            
          last_iter = iter;
        }
        
        int max_profit_sum = 0;
        for (int work : worker) {
            auto target_difficulty_iter = difficulty_to_profit.upper_bound(work);
            if (target_difficulty_iter == difficulty_to_profit.begin()) {
                continue;
            }
            --target_difficulty_iter;
            max_profit_sum += target_difficulty_iter->second;
        }
        
        return max_profit_sum;
    }
};

Code的写法不如这个优雅：https://www.cnblogs.com/grandyang/p/10264877.html