最小生成树算法——Kruskal算法、Prim算法、堆优化的Prim算法

什么叫最小生成树？
已知一个无向连通图，那么这个图的最小生成树是该图的一个子图，且这个子图是一棵树且把图中所有节点连接到一起了。一个图可能拥有多个生成树。一个带权重的无向连通图的最小生成树（minimum spanning tree），它的权重和是小于等于其他所有生成树的权重和的。
生成树的权重和，是把生成树的每条边上的权重加起来的和。

一颗最小生成树有多少条边？
已知带权重无向连通图有V个节点，那么图的最小生成树的边则有V-1条边。

最小生成树有哪些应用？
具体在这里Applications of Minimum Spanning Tree Problem，就不翻译了，大家自行阅读吧==

Kruskal算法

思路

步骤如下：
1.以每条边的权重排序，排非降序。
2.每次挑选一个权重最小的边，检查将其加入到最小生成树时，是否会形成环（一颗树是没有环的啊）
3.重复步骤2直到最小生成树中有V-1条边。
在步骤2中，我们使用Union-Find algorithm来检测加入边是否会形成环。

显而易见，Kruskal算法是一种贪心算法，以下面例子开始实际讲解。

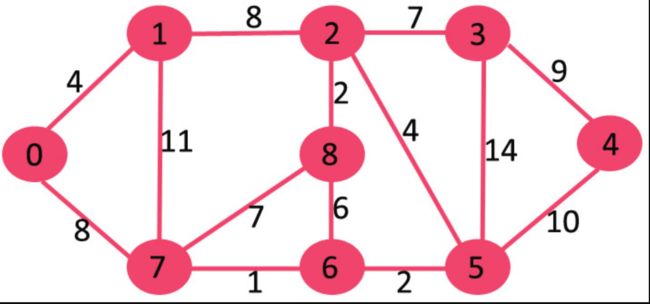
此图包含9个节点和14条边，所以该图的最小生成树会有（9-1）=8条边。该示例的处理步骤如下：
1. 挑选边7-6，此时没有环形成，则加入这条边。

2. 挑选边8-2，此时没有环形成，则加入这条边。

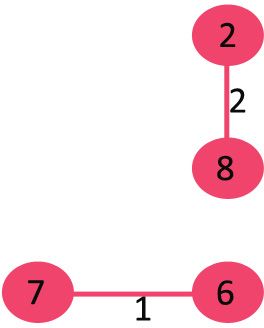
3. 挑选边6-5，此时没有环形成，则加入这条边。

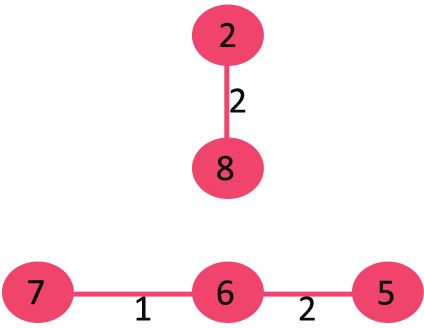
4. 挑选边0-1，此时没有环形成，则加入这条边。

5. 挑选边2-5，此时没有环形成，则加入这条边。

6. 挑选边8-6，此时有环形成，则不加入这条边。
7. 挑选边2-3，此时没有环形成，则加入这条边。

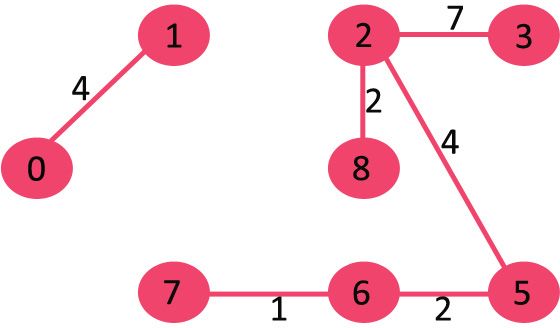
8. 挑选边7-8，此时有环形成，则不加入这条边。
9. 挑选边0-7，此时没有环形成，则加入这条边。

10. 挑选边1-2，此时有环形成，则不加入这条边。
11. 挑选边3-4，此时没有环形成，则加入这条边。

运行到这里，已经包含了8条边，所以算法终止。

代码

代码来自Kruskal’s Minimum Spanning Tree Algorithm。

from collections import defaultdict

class Graph:

    def __init__(self,vertices):
        self.V= vertices #顶点的数量
        self.graph = [] # 二维list用来存边的起点、终点、权重

    # 添加每条边
    def addEdge(self,u,v,w):
        self.graph.append([u,v,w])

    # 递归找到每个节点所在子树的根节点
    def find(self, parent, i):
        if parent[i] == i:
            return i
        return self.find(parent, parent[i])

    # 联合两颗子树为一颗子树，谁附在谁身上的依据是rank
    def union(self, parent, rank, x, y):
        xroot = self.find(parent, x)
        yroot = self.find(parent, y)

        #进行路径压缩
        if(xroot != parent[x]):
            parent[x] = xroot
        if(yroot != parent[y]):
            parent[y] = yroot 

        # 将较小rank的子树附在较大rank的子树上去
        if rank[xroot] < rank[yroot]:
            parent[xroot] = yroot
        elif rank[xroot] > rank[yroot]:
            parent[yroot] = xroot

        # 若rank一样，程序这里写死即可
        else :
            parent[yroot] = xroot
            rank[xroot] += 1

    # 主函数用来构造最小生成树
    def KruskalMST(self):

        result =[] #存MST的每条边

        i = 0 # 用来遍历原图中的每条边，但一般情况都遍历不完
        e = 0 # 用来判断当前最小生成树的边数是否已经等于V-1

        #按照权重对每条边进行排序，如果不能改变给的图，那么就创建一个副本，内建函数sorted返回的是一个副本
        self.graph =  sorted(self.graph,key=lambda item: item[2])

        parent = [] ; rank = []

        # 创建V个子树，都只包含一个节点
        for node in range(self.V):
            parent.append(node)
            rank.append(0)

        # MST的最终边数将为V-1
        while e < self.V -1 :

            # 选择权值最小的边，这里已经排好序
            u,v,w =  self.graph[i]
            i = i + 1
            x = self.find(parent, u)
            y = self.find(parent ,v)

            # 如果没形成边，则记录下来这条边
            if x != y:
                #不等于才代表没有环
                e = e + 1    
                result.append([u,v,w])
                self.union(parent, rank, x, y)            
            # 否则就抛弃这条边

        print ("Following are the edges in the constructed MST")
        for u,v,weight  in result:
            print ("%d -- %d == %d" % (u,v,weight))

g = Graph(4)
g.addEdge(0, 1, 10)
g.addEdge(0, 2, 6)
g.addEdge(0, 3, 5)
g.addEdge(1, 3, 15)
g.addEdge(2, 3, 4)
#虽然是无向图，但每条边只存一次
g.KruskalMST()

加了一些必要的中文注释，关于检测环的思路具体请参考Union-Find algorithm，不过值得注意的是，原代码并没有路径压缩（来自Union-Find）的操作，是我自己加上的。

代码优化

发现一处可以优化的地方，就是在union函数中会重复寻找两个节点所在子树的根节点，而这两个根节点已经在主函数KruskalMST中的while循环中就被找到了（u的根是x，v的根是y），所以，在union函数中应该有四个参数，分别是两个点以及对应的两个根节点。
修改后可以避免每次循环中，两次union函数的重复调用。
修改如下：
KruskalMST中的while循环中的这句self.union(parent, rank, x, y)修改成self.union(parent, rank, u, v, x, y)。
union函数修改为：

    def union(self, parent, rank, x, y, xroot, yroot):
        #xroot = self.find(parent, x)不需要重复此函数
        #yroot = self.find(parent, y)不需要重复此函数

        #进行路径压缩
        if(xroot != parent[x]):
            parent[x] = xroot
        if(yroot != parent[y]):
            parent[y] = yroot 

        # Attach smaller rank tree under root of high rank tree (Union by Rank)
        if rank[xroot] < rank[yroot]:
            parent[xroot] = yroot
        elif rank[xroot] > rank[yroot]:
            parent[yroot] = xroot

        # If ranks are same, then make one as root and increment its rank by one
        else :
            parent[yroot] = xroot
            rank[xroot] += 1

Prim算法

思路

prim算法也是一种贪心算法。开始时，最小生成树（MST）为空（不包含任何节点），然后维持两个集合，一个集合是包含已经进入MST中的节点，另一个集合时包含未被加入到MST中的节点。在算法的每个步骤中，从连接这两个集合的所有边中，挑选一个最小权值的边。在挑选之后，要把这条边上不在MST中的另一个节点加入到MST中去。
注意，连接这两个集合的所有边，肯定是一个节点在MST集合中，另一个节点在非MST集合中。

Prim算法的思想：首先要考虑连通性，最小生成树中的每条边，在原图中肯定也是已存在的边。然后通过连接MST集合和非MST集合中的节点来生成最小生成树。在连接的过程中，必须挑选最小权值的边来连接。

Prim算法的步骤：（节点个数为V）
1.创建一个集合mstSet用来判断是否所有节点都已经被包括到MST中，当集合大小为V时，则MST包括了所有节点。
2.根据原图边的权重为每个节点分配一个key值，初始时每个节点的key值都是无穷大，当0节点作为第一个被挑选的节点时，将0节点的key值赋值为0。
3.只要当mstSet还没有包含所有节点时，就重复以下步骤：
…(i)选择一个节点u，u是非MST集合中key值最小的那个节点。
…(ii)把u加入到mstSet。
…(iii)更新u节点的邻接点v的key值。遍历u的邻接点v，每当边u-v的权值小于v的key值时，就更新v的key值为边u-v的权值，同时记录下v的父节点为u。

实际例子处理步骤：
已知带权值的无向连通图如下：

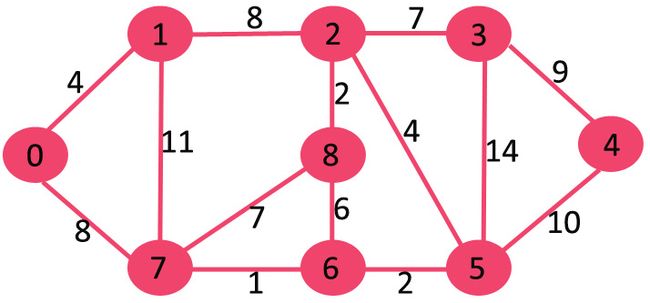
初始时，mstSet为空，每个节点的key值为{0, INF, INF, INF, INF, INF, INF, INF}，INF代表无穷大。现在挑选具有最小key值的节点，所以0节点被挑选，将其加入到mstSet中。所以mstSet现在为{0}。
在加入节点到mstSet中后，更新邻接点的key值，0的邻接点为1和7，然后1和7的key值分别被更新为4和8。
图中只显示出key值为有限值的节点。绿色节点代表在mstSet集合中的节点。

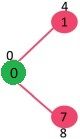
挑选不在mstSet集合中的key值最小的那个节点。1被挑选且加入到mstSet中去，mstSet变成{0, 1}。更新1的邻接点的key值，所以2的key值变成8.

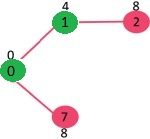
挑选不在mstSet集合中的key值最小的那个节点。看上图发现，我们既可以挑选2节点，也可以挑选7节点，此时挑选7节点。mstSet变成{0, 1, 7}。更新7的邻接点的key值，所以6和8的key值分别变成7和1。

挑选不在mstSet集合中的key值最小的那个节点。6被挑选且加入到mstSet中去，mstSet变成{0, 1, 7, 6}。更新6的邻接点的key值，所以5和8的key值分别变成2和6。

重复以上步骤，直到mstSet包含了所有的节点。

代码

代码给定的图如下，使用python3，代码来自Prim’s Minimum Spanning Tree，稍作修改且加上了中文注释：

class Graph():

    def __init__(self, vertices):
        self.V = vertices
        self.graph = [[0 for column in range(vertices)] 
                      for row in range(vertices)]

    # 使用parent[]来打印MST
    def printMST(self, parent):
        print ("Edge \tWeight")
        #打印每个点与父节点的边就可以了，注意根节点不用打印
        for i in range(1,self.V):
            print (parent[i],"-",i,"\t",self.graph[i][ parent[i] ])

    # 在非MST集合中选择具有最小key值的节点
    def minKey(self, key, mstSet):

        min = float("inf")

        for v in range(self.V):
            if key[v] < min and mstSet[v] == False:
            #False代表是非MST集合中的节点，然后就是普通的寻找最小的操作
                min = key[v]
                min_index = v

        return min_index

    # 主函数，用来构造MST
    def primMST(self):
        #每个节点分配一个key值，在cut图中用来挑选最小权值的那条边，初始为无穷大
        key = [float("inf")] * self.V
        parent = [None] * self.V # 数组用来记录每个节点的父节点
        key[0] = 0   # 挑选0节点作为选择的起点
        mstSet = [False] * self.V#记录每个节点是否被加入到了MST集合中

        parent[0] = -1  # 第一个节点作为树的根节点

        for cout in range(self.V):

            # 从非MST集合中挑选最小距离的节点
            u = self.minKey(key, mstSet)

            # 把挑选到的节点放到MST集合中去
            mstSet[u] = True

            # 更新被挑选节点的邻接点的距离，只有当新距离比当前距离要小，且这个邻接点在非MST集合中
            for v in range(self.V):
                # self.graph[u][v] > 0代表v是u的邻接点
                # mstSet[v] == False代表当前节点还没有加入到MST中
                # key[v] > self.graph[u][v]只有新距离比当前记录距离要小时更新
                # 两种情况，一是key[v]为无穷，肯定更新；二是key[v]为常数，但新距离更小
                if (self.graph[u][v] > 0) and (mstSet[v] == False) and (key[v] > self.graph[u][v]):
                        key[v] = self.graph[u][v]#更新距离
                        parent[v] = u#更新父节点

        self.printMST(parent)

g  = Graph(5)
g.graph = [ [0, 2, 0, 6, 0],
             [2, 0, 3, 8, 5],
             [0, 3, 0, 0, 7],
             [6, 8, 0, 0, 9],
             [0, 5, 7, 9, 0],
           ]
#图的表示用邻接矩阵，根据矩阵元素的索引判断是哪条边
#根据矩阵元素判断该边是否有边，不为0代表有边

g.primMST();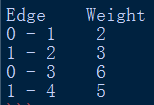

注意，对节点u的邻接点v进行key值的减小，这里一般称为对v进行松弛操作，松弛操作类似最短路径算法的松弛操作。

思考与总结

Kruskal算法因为是从所有边中挑选权值最小的边，所以在每次加入边的时候，需要判断是否形成环。
Prim算法相比Kruskal算法的优势在于，Prim算法考虑边的连通性（Kruskal从所有边中挑选，而Prim从连通的边中挑选）。
而且Prim算法不用考虑在加入节点的过程中，是否会形成环。形成环的条件是图中有回边（back edge），但每次挑选节点加入mstSet中时，都是从非MST集合中挑选，所以不可能让更新后的最小生成树形成回边。
需要排序的次数不同：Kruskal算法是在算法开始前对所有边的权值进行排序，但就这一次排序。Prim算法是每次挑选节点时，都需要进行排序，但每次排序都是一部分边就行。明显可见，Prim算法排序的总次数，肯定比Kruskal算法排序的总次数要多。
Kruskal算法时间复杂度：为O(ElogE)或者O(ElogV)。排序所有边需要O(ELogE)的时间，排序后，还需要对所有边应用Union-find算法，Union-find操作最多需要O(LogV)时间，再乘以边数E，所以就是O(ElogV)。
所以总共需要O(ELogE + ELogV) 时间。由于一般图中，边数E是大约为O( V2 V 2 ):，所以O(LogV)和 O(LogE)是大约一样的。PS:这句话从Kruskal算法看来的，我也没看懂，但有了这两个条件，推导过程如下：

所以，时间复杂度为O(ElogE)或者O(ElogV)，一般认为是前者。
Prim算法时间复杂度：为O( V2 V 2 )。如果输入的图，用邻接表表示，且使用了二叉堆（binary heap）的数据结构，复杂度能降到O(E log V)或O(V log V)。

适用范围：Prim一般用于稠密图，因为其复杂度为O(V log V)，则主要取决于点数，而与边数无关。Kruskal一般用于稀疏图，因为其复杂度为O(ElogE)，则主要取决于边数，而与点数无关。

堆优化的Prim算法

思路

上面提到，如果使用二叉堆，prim算法的复杂度能降到O(E log V)，接下来本文将讲解使用堆优化的Prim算法。
之前实现的这个Prim算法，是用邻接矩阵表示图。而堆优化的Prim算法，将用邻接表来表示图，且使用最小堆来寻找，连接MST集合和非MST集合的边中，最小权值的那条边。
基本思想：基本思想和原Prim算法大体相同，但此算法是，根据邻接表，通过广度优先遍历（BFS）来遍历所有节点，遍历的总操作为O(V+E)次数。同时使用最小堆存储非MST集合中的节点，每次遍历时用最小堆来选择节点。最小堆操作的时间复杂度为O(LogV)。
基本步骤：
1.创建一个大小为V的最小堆，V是图的节点个数。最小堆的每个元素，存储的是节点id和节点的key值。
2.初始化时，让堆的第一个元素作为最小生成树的根节点，赋值根节点的key值为0。其余节点的key值赋值为无穷大。
3.只要最小堆不为空，就重复以下步骤：
…(i)从最小堆中，抽取最小key值的节点，作为u。
…(ii)对于u的每个邻接点v，检查v是否在最小堆中（即还没有加入到MST中）。如果v在最小堆中，且v的key值是大于边u-v的权值时，就更新v的key值为边u-v的权值。
实际例子处理步骤：
与上面Prim算法的一样。

代码

代码来自Prim’s MST using min heap，稍微修改，因为原本是python2的代码，且加上了中文注释方便读者理解。
已知带权值的无向连通图如下：

from collections import defaultdict

class Heap():

    def __init__(self):
        self.array = []#用数组形式存储堆的树结构
        self.size = 0#堆内节点个数
        self.pos = []#判断节点是否在堆中

    def newMinHeapNode(self, v, dist):
        minHeapNode = [v, dist]
        return minHeapNode

    # 交换堆中两个节点
    def swapMinHeapNode(self, a, b):
        t = self.array[a]
        self.array[a] = self.array[b]
        self.array[b] = t

    def minHeapify(self, idx):#递归，下滤根节点
        #符合完全二叉树中，索引规律
        smallest = idx
        left = 2 * idx + 1
        right = 2 * idx + 2
        print(self.array,self.size)
        print(self.pos)

        if left < self.size and self.array[left][1] < \
                                self.array[smallest][1]:
            smallest = left

        if right < self.size and self.array[right][1] < \
                                self.array[smallest][1]:
            smallest = right
        #最终smallest为三个点中最小的那个的索引，非左即右

        # smallest将与左或右节点交换
        if smallest != idx:

            # Swap positions
            self.pos[ self.array[smallest][0] ] = idx
            self.pos[ self.array[idx][0] ] = smallest

            # Swap nodes
            self.swapMinHeapNode(smallest, idx)

            self.minHeapify(smallest)

    # 抽取堆中最小节点
    def extractMin(self):

        if self.isEmpty() == True:
            return

        # 找到根节点
        root = self.array[0]

        # 把最后一个节点放在根节点上去
        lastNode = self.array[self.size - 1]
        self.array[0] = lastNode
        print()
        print('当前堆最后面位置的元素为',lastNode)

        # 更新根节点和最后一个节点的pos
        self.pos[lastNode[0]] = 0
        self.pos[root[0]] = self.size - 1#此时堆大小已经减小1

        # 减小size，从根节点开始从新构造
        self.size -= 1
        self.minHeapify(0)

        return root#返回的是被替换掉的那个

    def isEmpty(self):
        return True if self.size == 0 else False

    def decreaseKey(self, v, dist):#上滤节点

        # 获得v在堆中的位置
        i = self.pos[v]

        # 更新堆中v的距离为dist，虽说是更新，但肯定是减小key
        self.array[i][1] = dist

        # 一直寻找i的父节点，检查父节点是否更大
        while i > 0 and self.array[i][1] < self.array[int((i - 1) / 2)][1]:

            # pos数组交换，array也得交换
            self.pos[ self.array[i][0] ] = int((i-1)/2)
            self.pos[ self.array[int((i-1)/2)][0] ] = i
            self.swapMinHeapNode(i, int((i - 1)/2) )

            # i赋值为父节点索引
            i = int((i - 1) / 2)

    # 检查v是否在堆中，很巧妙的是，由于size一直在减小
    # 当pos小于size说明该点在堆中不可能的位置，即不在堆中
    def isInMinHeap(self, v):

        if self.pos[v] < self.size:
            return True
        return False


def printArr(parent, n):
    for i in range(1, n):
        print ("% d - % d" % (parent[i], i))


class Graph():

    def __init__(self, V):
        self.V = V
        self.graph = defaultdict(list)

    # 添加无向图的每条边
    def addEdge(self, src, dest, weight):

        # 当前边从src到dest，权值为weight
        # 添加到src的邻接表中，添加元素为[dest, weight]
        # 注意都是添加到0索引位置
        newNode = [dest, weight]
        self.graph[src].insert(0, newNode)

        # 因为是无向图，所以反向边也得添加
        newNode = [src, weight]
        self.graph[dest].insert(0, newNode)

    # 主函数用来构造最小生死树（MST）
    def PrimMST(self):
        # V是节点的个数
        V = self.V  

        # 存每个节点的key值
        key = []   

        # 记录构造的MST
        parent = [] 

        # 建立最小堆
        minHeap = Heap()

        # 初始化以上三个数据结构
        for v in range(V):
            parent.append(-1)#初始时，每个节点的父节点是-1
            key.append(float('inf'))#初始时，每个节点的key值都是无穷大
            minHeap.array.append( minHeap.newMinHeapNode(v, key[v]) )
            #newMinHeapNode方法返回一个list，包括节点id、节点key值
            #minHeap.array成员存储每个list，所以是二维list
            #所以初始时堆里的每个节点的key值都是无穷大
            minHeap.pos.append(v)
            #pos成员添加每个节点id
        #minHeap.pos初始时是0-8，都小于9即节点数

        minHeap.pos[0] = 0#不懂这句，本来pos的0索引元素就是0啊
        key[0] = 0#让0节点作为第一个被挑选的节点
        minHeap.decreaseKey(0, key[0])
        #把堆中0位置的key值变成key[0]，函数内部重构堆

        # 初始化堆的大小为V即节点个数
        minHeap.size = V
        print('初始时array为',minHeap.array)
        print('初始时pos为',minHeap.pos)
        print('初始时size为',minHeap.size)

        # 最小堆包含所有非MST集合中的节点
        # 所以当最小堆为空，循环终止
        while minHeap.isEmpty() == False:

            # 抽取最小堆中key值最小的节点
            newHeapNode = minHeap.extractMin()
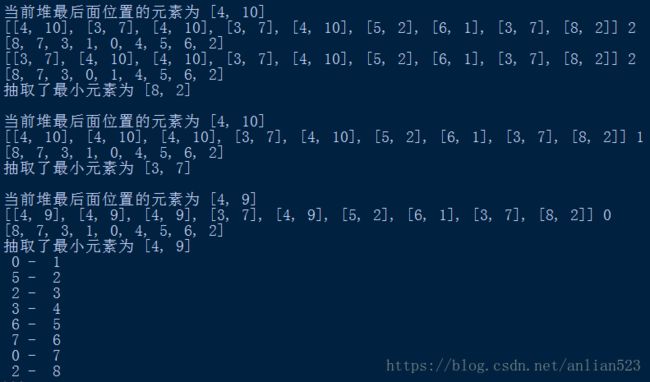
            print('抽取了最小元素为',newHeapNode)
            u = newHeapNode[0]

            # 遍历所有的邻接点然后更新它们的key值
            for pCrawl in self.graph[u]:

                v = pCrawl[0]

                # 如果v在当前最小堆中，且新的key值比当前key值更小，就更新
                if minHeap.isInMinHeap(v) and pCrawl[1] < key[v]:
                    key[v] = pCrawl[1]
                    parent[v] = u

                    # 也更新最小堆中节点的key值，重构
                    minHeap.decreaseKey(v, key[v])

        printArr(parent, V)

graph = Graph(9)
graph.addEdge(0, 1, 4)
graph.addEdge(0, 7, 8)
graph.addEdge(1, 2, 8)
graph.addEdge(1, 7, 11)
graph.addEdge(2, 3, 7)
graph.addEdge(2, 8, 2)
graph.addEdge(2, 5, 4)
graph.addEdge(3, 4, 9)
graph.addEdge(3, 5, 14)
graph.addEdge(4, 5, 10)
graph.addEdge(5, 6, 2)
graph.addEdge(6, 7, 1)
graph.addEdge(6, 8, 6)
graph.addEdge(7, 8, 7)
graph.PrimMST()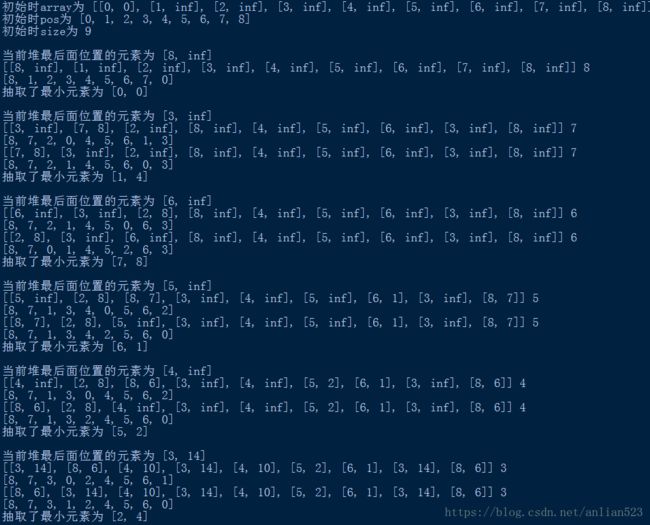

分析代码：
由于堆的本质是一颗完全二叉树，而完全二叉树的父节点的索引与其左右孩子的索引之间，具有良好运算关系，如下图所示：

若某节点索引为x，那么其左孩子索引为2*x+1，其右孩子索引为2*x+2。观察上图发现此运算关系成立，所以上图所示完全二叉树则可以一个数组[0,1,2,3,4,5,6]来表示，而不需要真的建立一种树的数据结构。

首先看程序中的数据结构：
..0)若节点个数为V，则这V个节点id为[0,1,2…V-1]。分别称为节点0、节点1、节点2、… 、节点V-1.
..1)在PrimMST函数中的key数组：与原Prim算法中的一样，用来记录每个节点的key值。
..2)在PrimMST函数中的parent数组：与原Prim算法中的一样，用来记录最小生成树。
..3)在minHeap对象中的size（整数型）：代表当前堆的大小，初始时size为V。以当前例子分析，初始时，size为9（原图一共有9个点），每当将一个点加入MST中后，size就会减小1。
..4)在minHeap对象中的pos数组：position，节点在最小堆中位置，大小为V。其索引i代表的是节点i，而pos[i]代表的是节点i在堆中的位置。比如pos[0]=3，则代表节点0处在堆中索引为3的位置上。且pos[i]需要和size配合使用：当pos[i]时，代表节点i在堆的pos[i]的索引的位置上；当pos[i]>=size时，代表节点i已经不在堆中了，而是已经加入到了最小生成树中了。以当前例子分析，初始时，pos为[0,1,2…8]。
..5)在minHeap对象中的array数组：用这个数组来表示堆，由于之前提到的完全二叉树的良好性质，大小为V。其索引i代表的是堆中的各个位置，而array[i]代表的是，在堆的i索引位置存的节点以及该节点的key值。且array[i]需要和size配合使用：对于小于size的i，这些array[i]都是堆中的元素；对于大于等于size的i，这些array[i]都不能看因为没有意义（注意它们不是加入到MST中的元素，因为程序是这么设计）。
初始时，array数组是符合最小堆定义的，因为堆的0位置元素的key值为0，其余位置元素的key值为INF。而且值得注意的是，在程序执行过程中，一般都是这个堆除了前几个元素的key值都为有限数字以外，其余元素的key值都为INF，这是因为，连接MST集合与非MST集合的边是有限的，属于非MST集合的节点组成了堆，但只有这些边在非MST集合那头的节点的key才会是有限数字。

再看程序中函数的功能：
..1)PrimMST函数：主函数，用来构造最小生成树，生成必须的数据结构，并对其进行初始化。其中的while循环是其主要功能，每次循环中，抽取最小堆的根节点（即最小的key值的节点，此时最小堆已构建好）作为u，遍历u的邻接表即遍历u的每个邻接点v，判断是否需要更新v的key值，是则更新key值，即对v进行松弛操作。
..2)extractMin函数：抽取最小堆的根节点root作为返回值，然后将root替换为堆中最后一个元素lastNode，size大小减小1，在函数的最后执行minHeapify函数，最后return。
..3)minHeapify函数：在替换root替换为堆中最后一个元素lastNode后，需要对堆重新构造，使其保持最小堆性质。 此函数是一个递归函数，功能为将根节点在堆中下滤，递归到不能下滤为止。
..4)decreaseKey函数：用于更新u的邻接点v的key值，而且顾名思义，肯定是减小key值。此函数功能为，将某更新过key值的节点在堆中上滤，此函数不用设计成递归的原因是，上滤最多能到达根节点，而下滤是没有一个明确的终点的。
minHeapify函数和decreaseKey函数都是为了，在改变堆后，使得堆保持最小堆的性质。

时间复杂度分析：
观察PrimMST函数的内部循环，因为在遍历节点的过程类似BFS，所以是被执行O(V+E)次数。在内部循环中，decreaseKey函数被执行，其执行时间为O(LogV)。所以总时间为O(E+V)*O(LogV)=O(ELogV) ，因为一般连通图中V = O(E)。