机器学习sklearn(学习笔记5)——决策树3
机器学习sklearn(学习笔记5)——决策树3
- 分类
- 回归
- 多头输出问题
- 复杂性
- 决策树的算法:ID3、C4.5、C5.0、CART
- ID3
- C4.5
- C5.0
决策树(DTs)是用于分类和回归的非参数监督学习方法。 目标是创建一个模型,通过学习从数据特征推断出的简单决策规则来预测目标变量的值。
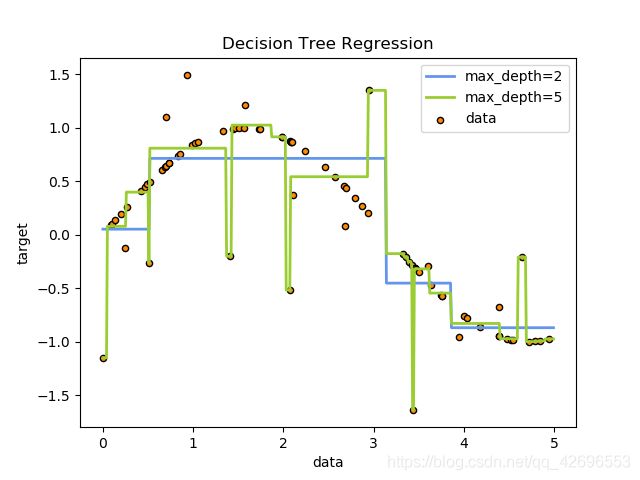
例如,在下面的示例中,决策树从数据中学习如何使用一组if-then-else决策规则中的数据近似正弦曲线。树越深,决策规则越复杂,模型越合适。
决策树的一些优点:
- 易于理解和解释。决策树可以可视化。
- 几乎不需要数据预处理。其他方法经常需要数据标准化,创建虚拟变量和删除缺失值。决策树还不支持缺失值。
- 使用树的花费(例如预测数据)是训练数据点(data points)数量的对数。
- 可以同时处理数值变量和分类变量。其他方法大都适用于分析一种变量的集合。
- 可以处理多值输出变量问题。
- 使用白盒模型。如果一个情况被观察到,使用逻辑判断容易表示这种规则。相反,如果是黑盒模型(例如人工神经网络),结果会非常难解释。
- 可以使用统计检验检验模型。这样做被认为是提高模型的可行度。 即使对真实模型来说,假设无效的情况下,也可以较好的适用。
决策树的一些缺点:
- 决策树学习可能创建一个过于复杂的树,并不能很好的预测数据。也就是过拟合。修剪机制(现在不支持),设置一个叶子节点需要的最小样本数量,或者数的最大深度,可以避免过拟合。
- 决策树可能是不稳定的,因为即使非常小的变异,可能会产生一颗完全不同的树。这个问题通过decision trees with an ensemble来缓解。
- 学习一颗最优的决策树是一个NP-完全问题under several aspects of optimality and even for simple concepts。因此,传统决策树算法基于启发式算法,例如贪婪算法,即每个节点创建最优决策。这些算法不能产生一个全家最优的决策树。对样本和特征随机抽样可以降低整体效果偏差。
- 概念难以学习,因为决策树没有很好的解释他们,例如,XOR, parity or multiplexer problems.
- 如果某些分类占优势,决策树将会创建一棵有偏差的树。因此,建议在训练之前,先抽样使样本均衡。
分类
DecisionTreeClassifier 能够对数据进行多分类的类。
和其他分类器一样,DecisionTreeClassifier 有两个向量输入:X,稀疏或密集,大小为[n_sample,n_fearure],存放训练样本; Y,值为整型,大小为[n_sample],存放训练样本的分类标签:
>>> from sklearn import tree
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)
拟合后,模型可以用来预测分类:
>>> clf.predict([[2., 2.]])
array([1])
另外,每个分类的概率可以被预测,即某个叶子中,该分类样本的占比。
>>> clf.predict_proba([[2., 2.]])
array([[ 0., 1.]])
DecisionTreeClassifier 能同事应用于二分类(标签为[-1,1])和多分类(标签为[0,1,K-1])。
用数据集 lris ,可以构造下面的树:
>>> from sklearn.datasets import load_iris
>>> from sklearn import tree
>>> iris = load_iris()
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(iris.data, iris.target)
训练完成后,我们可以用export_graphviz将决策树输出到Graphviz。下面是在整个iris数据集上训练的上述树的graphviz导出示例;结果保存在输出文件irs .pdf中:。
>>> import graphviz
>>> dot_data = tree.export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris")
export_graphviz导出器还支持多种美学选项,包括按类(或回归值)着色节点,如果需要,还可以使用显式变量和类名
>>> dot_data = tree.export_graphviz(clf, out_file=None,
... feature_names=iris.feature_names,
... class_names=iris.target_names,
... filled=True, rounded=True,
... special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph


范例【https://scikit-learn.org/stable/auto_examples/tree/plot_iris.html#sphx-glr-auto-examples-tree-plot-iris-py】
回归

决策树也被应用于回归问题,决策树分类
与分类设置一样,适合的方法将X和y作为参数数组。但在这种情况下,y应该是浮点值而不是整数值:
>>> from sklearn import tree
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])
参考范例【https://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression.html#sphx-glr-auto-examples-tree-plot-tree-regression-py】
多头输出问题
多输出问题是一个有多个输出可预测的监督学习问题
当输出之间没有相关性时,解决这类问题的一个非常简单的方法是建立n个独立的模型,即每个输出一个,然后使用这些模型独立地预测n个输出中的每一个。然而,由于可能与相同输入相关的输出值本身是相关的,因此通常更好的方法是构建一个能够同时预测所有n个输出的单一模型。首先,它需要更短的训练时间,因为只构建了一个评估器。其次,结果估计器的泛化精度往往会提高。
对于决策树,这种策略可以很容易地用于支持多输出问题。这需要作出以下改变:
- 将n的输出值存储在叶子中,而不是1;
- 使用分裂准则计算所有n个输出的平均减少量。
该模块通过在DecisionTreeClassifier和DecisionTreeRegressor中实现此策略,为多输出问题提供了支持。如果决策树适合大小为[n_samples, n_output]的输出数组Y,则结果估计器将:
- 输出n_output值预测;
- 根据predict_proba输出类概率的n_output数组列表。
在多输出决策树回归中,应用多输出树进行回归。在这个例子中,输入X是一个实值,输出Y是sin和cos X。

在人脸补全过程中,利用多输出树进行分类,并给出了多输出估计量。在这个例子中,输入X是人脸上半部分的像素,输出Y是人脸下半部分的像素。

参考案例【https://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression_multioutput.html#sphx-glr-auto-examples-tree-plot-tree-regression-multioutput-py】
参考案例【https://scikit-learn.org/stable/auto_examples/plot_multioutput_face_completion.html#sphx-glr-auto-examples-plot-multioutput-face-completion-py】
复杂性
一般来说,构建一个运行时成本平衡二叉树是O (nsamplesnfeatureslog(nsamples))和查询时间O (log(nsamples))。虽然树构造算法试图生成平衡的树,但它们并不总是平衡的。假设子树保持近似平衡,每个节点的代价包括通过O(nfeatures)搜索提供最大熵减少的特性。这一成本O (nfeaturesnsampleslog(nsamples))在每个节点,导致总成本在整个树(在每个节点通过加总成本)的O (nfeaturesn2sampleslog(nsamples))。
Scikit-learn为构建决策树提供了一个更有效的实现。一个简单的实现(如上所述)将重新计算类标签直方图(用于分类)或平均值(用于回归)在每个新的分界点沿着给定的特性。在所有相关样品预分类的特征,保留运行标签数,将减少每个节点的复杂度O (nfeatureslog(nsamples)),从而导致总成本的O (nfeaturesnsampleslog(nsamples))。这是所有基于树的算法的一个选项。默认情况下,它是用于梯度增强的,一般来说,它使训练更快,但关闭了所有其他算法,因为当训练深度树时,它往往会减慢训练速度。
决策树的算法:ID3、C4.5、C5.0、CART
所有不同的决策树算法是什么?它们之间有什么不同?哪个是在scikit-learn中实现的?
ID3
ID3(迭代二分法3)是1986年由Ross Quinlan开发的。该算法创建一个多路树,为每个节点(即以贪婪的方式)找到分类特征,从而为分类目标获得最大的信息增益。树被生长到最大尺寸,然后通常使用修剪步骤来提高树对不可见数据的泛化能力。
C4.5
C4.5是ID3的继承者,它通过动态定义一个离散属性(基于数值变量),将连续属性值划分为一组离散的区间,从而消除了特性必须分类的限制。C4.5将训练好的树(即ID3算法的输出)转换为if-then规则集。然后评估每个规则的准确性,以确定应用规则的顺序。剪枝是通过删除规则的先决条件来完成的,前提是如果没有规则,规则的准确性就会提高。
C5.0
C5.0是昆兰的最新版本,是在专有许可下发布的。与C4.5相比,它使用的内存更少,构建的规则集也更小,同时也更准确。
CART(分类和回归树)与C4.5非常相似,但不同之处在于它支持数值目标变量(回归),并且不计算规则集。CART使用在每个节点上产生最大信息增益的特性和阈值构造二叉树。
scikit-learn使用了CART算法的优化版本;然而,scikit-learn实现目前还不支持分类变量。
翻译来源【https://scikit-learn.org/stable/modules/tree.html】