埃塞托尼亚筛和欧拉筛详解

素数相关详解

本文讲解了素数 的定义
并且从素数的暴力算法优化到了欧拉筛法
更多博客，可以去往我的个人博客（传送门）https://hacv.gitee.io/

目录

• 1.素数的定义
• 2.素数相关算法

• 判别素数的朴素法（暴力法）

• 算法原理
• 实现(轻微优化)

• 埃塞托尼亚筛

• 算法原理
• 实现1
• 实现2：对实现1的优化

• 欧拉筛

• 算法原理
• 实现

• 3.其他

1.素数的定义

维基百科定义：
质数（Prime number），又称素数，指在大于1的自然数中，除了1和该数自身外，无法被其他自然数整除的数（也可定义为只有1与该数本身两个正因数的数）。大于1的自然数若不是素数，则称之为合数（也称为合成数）。

Tips：

1.有的教材上：（指在大于1的自然数中）这一点没有强调，导致容易误解！！！
也是经常弄晕一些人对素数的理解的原因。
2.注意：

1既不是素数也不是合数！！！

2.素数相关算法

• 判别素数的朴素法（暴力法）

1）算法原理：

不管三七二十一
根据素数定义就是一顿暴力。

2）实现(轻微优化)

轻微优化处：其实就是将从2扫描到n改善为了从2扫描到sqrt（n）
原因：假设n%k=0 则有 n * ( n / k) == n

代码段：

int isPrime(int n)
{
	//0表示不是素数，1表示是素数 
	if(n<=1)
	return 0; 
	//表示根号n向下取整 
	int sqrt_num=(int)sqrt(1.0*n);
	
	for(int i=2;i<=sqrt_num;i++)
	{
		if(n%i==0)
		{
			return 0;
		}
	 } 
	
	return 1;//是素数 
}

• 埃塞托尼亚筛

1）算法原理：

1>假设从2-N全是素数
2>从2开始枚举，对于每个素数，我们筛去它的所有倍数，最后我们剩下来的就都是素数
关键点：
从2开始枚举到某个数字A，如果a没有被前面步骤的数筛去，那么a一定是素数。
原因：
如果A(A>2)是合数，则A=素数×另一个数
PS：这个素数必定小于A，所以会被我们前面筛出来的素数筛掉

2）实现

用一个标记数组实现
枚举的过程中，筛的过程就是依次改变这个标记数组的过程

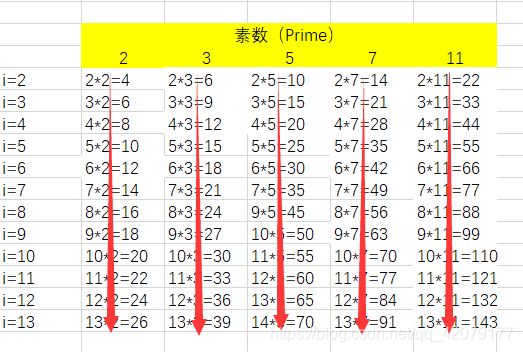
实现1：按照思路直接筛，筛的过程如下图红色箭头所示

代码段：

//Eratosthenes_one.cpp 
#include
const int maxn=100000+5;

//除了0,1之外(因为0和1既不是合数，也不是素数)
//TagArray数组中，0表示i是素数，1表示是合数
int TagArray[maxn]={0};

//Prime数组中存放素数(从0号位开始放)
//Num表示Prime数组中素数的个数 
int Prime[10000+5]={0};
int Num=0;

void FindPrime()
{
	for(int i=2;i<maxn;i++)
	{
		if(TagArray[i]==0)//如果标记数组说i这个数是素数 
		{
			Prime[Num++]=i;//存素数i，并且Num+1
			
			//注意这种写法，本来应该用i*j<=(maxn-1)判断就好了
			//但是要避免i*j的结果溢出int,所以改为j<=((maxn-1)/i)
			//maxn-1是因为标记数组范围本来就只有0-100004 
			for(int j=2; j<=((maxn-1)/i); ++j)
			{
				TagArray[j*i]=1;//筛去素数i的倍数 
			}
			
		}
	}
	
} 


int main()
{
	//求1-100000+4中哪些是素数
	FindPrime();
	printf("正整数100004内素数的个数:%d\n",Num);
	
	for(int i=0;i<Num;i++) 
	{
		printf("%d\n",Prime[i]);
	}
	
	
	return 0;
}

实现2：

在实现1的基础上，我们发现，如图中蓝色部分的，被重复筛了。我们容易观察出，如果要减少筛的次数，我们可以从质数的平方往后筛（优化）

代码段：

//Eratosthenes_two.cpp
#include
const int maxn=100000+5;

//除了0,1之外(因为0和1既不是合数，也不是素数)
//TagArray数组中，0表示i是素数，1表示是合数
int TagArray[maxn]={0};

//Prime数组中存放素数(从0号位开始放)
//Num表示Prime数组中素数的个数 
int Prime[10000+5]={0};
int Num=0;

void FindPrime()
{
	for(int i=2;i<maxn;i++)
	{
		if(TagArray[i]==0)//如果标记数组说i这个数是素数 
		{
			Prime[Num++]=i;//存素数i，并且Num+1
			
			//注意这种写法，本来应该用i*j<=(maxn-1)判断就好了
			//但是要避免i*j的结果溢出int,所以改为j<=((maxn-1)/i)
			//maxn-1是因为标记数组范围本来就只有0-100004 
//(修改处)将j=2改为了j=i，这样就能少筛掉表格中那些蓝色部分了 
			for(int j=i; j<=((maxn-1)/i); ++j) 
			{
				TagArray[j*i]=1;//筛去素数i的倍数 
			}
			
		}
	}
	
} 

//---------------main函数略，同前

• 欧拉筛

由来：
由于埃塞托尼亚筛筛的时候重复筛（比如下面的）了，使得算法效率还不够好，所以，我们改进一下，我们继续观察先前的图，发现埃塞托尼亚筛是竖着筛，我们似乎也难以优化这种筛法了，我们转换一下思路——横着筛，研究发现，我要是横着筛就会比前面那种只优化掉蓝色部分的埃氏筛还快

1）算法原理：

思路：在埃氏筛的一种优化
任何合数都能写成一个素数乘一个数（显然这个素数不一定是唯一的）
//举个例子：12=2×6=3×4（2和3都是素数，2是合数12的最小质因数）
所以，任何合数都有一个最小的质因数（这句话是核心）

用这个最小质因数来判断什么时候不用继续筛下去

那么如何实现呢？实现如下图：

注意：这里是横着筛，此外图中箭头从橙色出发（包括该点）往右的所有我都不筛
具体实现方法是用的一个break实现的。

2）实现

//Euler.cpp
#include
const int maxn=100000+5;

//除了0,1之外(因为0和1既不是合数，也不是素数)
//TagArray数组中，0表示i是素数，1表示是合数
int TagArray[maxn]={0};

//Prime数组中存放素数(从0号位开始放)
//Num表示Prime数组中素数的个数 
int Prime[10000+5]={0};
int Num=0;

void FindPrime()
{
	for(int i=2;i<maxn;i++)
	{
		if(TagArray[i]==0)//如果标记数组说i这个数是素数 
		{
			Prime[Num++]=i;//存素数，并且Num+1	
		}
		
		
		for(int j=0;(j<Num)&&(i<=((maxn-1)/Prime[j]));++j)
		{
			//一进来,不管三七二十一，先筛掉一个先
			TagArray[i*Prime[j]]=1;
			if(i%Prime[j]==0)
			{
				//判别i是Prime数组中某个的倍数，则跳出，
				//这行后面的也不用筛 	
				break;
			 } 	
			 
		 }
		
	}

} 

//---------------main函数略，同前

其他

1.判定素数暴力法一般用于小规模素数判断
2.埃氏筛和欧拉筛一般用于ACM比赛中获取大规模素数表
3.埃氏筛的时间复杂度是O（n*sqrt(n)）
4.欧拉筛的时间复杂度是O（n）