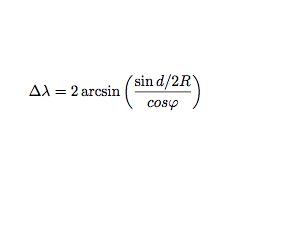java根据2个经纬度点，计算这2个经纬度点之间的距离(通过经度纬度得到距离)

最近做一个项目：需要查询一个站点（已知该站点经纬度）500米范围内的其它站点。所以，我首先想到的是，对每条记录，去进行遍历，跟数据库中的每一个点进行距离计算，当距离小于500米时，认为匹配。这样做确实能够得到结果，但是效率极其低下，因为每条记录都要去循环匹配n条数据，其消耗的时间可想而知。

于是我就想到一个先过滤出大概的经纬度范围再进行计算。比方说正方形的四个点，于是我在网上搜索，意外的，查询到了一个关于这个计算附近地点搜索初探，里面使用Python，PHP,C实现了这个想法。所以参考了一下原文中的算法，使用Java进行了实现。

实现原理也是很相似的，先算出该点周围的矩形的四个点，然后使用经纬度去直接匹配数据库中的记录。

思路：首先算出“给定坐标附近500米”这个范围的坐标范围。 虽然它是个圆，但我们可以先求出该圆的外接正方形，然后拿正方形的经纬度范围去搜索数据库。 图是我盗的：

 

值得一提的是，维基百科推荐使用Haversine公式，理由是Great-circle distance公式用到了大量余弦函数， 而两点间距离很短时（比如地球表面上相距几百米的两点），余弦函数会得出0.999...的结果， 会导致较大的舍入误差。而Haversine公式采用了正弦函数，即使距离很小，也能保持足够的有效数字。 以前采用三角函数表计算时的确会有这个问题，但经过实际验证，采用计算机来计算时，两个公式的区别不大。 稳妥起见，这里还是采用Haversine公式。

 

其中

 

• R为地球半径，可取平均值 6371km；
• φ1, φ2 表示两点的纬度；
• Δλ 表示两点经度的差值。
• 

 

import java.util.HashMap;
import java.util.Map;
  
public class MapDistance { 
        
    private static double EARTH_RADIUS = 6378.137; 
    
    private static double rad(double d) { 
        return d * Math.PI / 180.0; 
    }
      
    /**
     * 根据两个位置的经纬度，来计算两地的距离（单位为KM）
     * 参数为String类型
     * @param lat1 用户经度
     * @param lng1 用户纬度
     * @param lat2 商家经度
     * @param lng2 商家纬度
     * @return
     */
    public static String getDistance(String lat1Str, String lng1Str, String lat2Str, String lng2Str) {
        Double lat1 = Double.parseDouble(lat1Str);
        Double lng1 = Double.parseDouble(lng1Str);
        Double lat2 = Double.parseDouble(lat2Str);
        Double lng2 = Double.parseDouble(lng2Str);
          
        double radLat1 = rad(lat1);
        double radLat2 = rad(lat2);
        double difference = radLat1 - radLat2;
        double mdifference = rad(lng1) - rad(lng2);
        double distance = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(difference / 2), 2)
                + Math.cos(radLat1) * Math.cos(radLat2)
                * Math.pow(Math.sin(mdifference / 2), 2)));
        distance = distance * EARTH_RADIUS;
        distance = Math.round(distance * 10000) / 10000;
        String distanceStr = distance+"";
        distanceStr = distanceStr.
            substring(0, distanceStr.indexOf("."));
          
        return distanceStr;
    }
      
    /**
     * 获取当前用户一定距离以内的经纬度值
     * 单位米 return minLat
     * 最小经度 minLng
     * 最小纬度 maxLat
     * 最大经度 maxLng
     * 最大纬度 minLat
     */
    public static Map getAround(String latStr, String lngStr, String raidus) {
        Map map = new HashMap();
          
        Double latitude = Double.parseDouble(latStr);// 传值给经度
        Double longitude = Double.parseDouble(lngStr);// 传值给纬度
  
        Double degree = (24901 * 1609) / 360.0; // 获取每度
        double raidusMile = Double.parseDouble(raidus);
          
        Double mpdLng = Double.parseDouble((degree * Math.cos(latitude * (Math.PI / 180))+"").replace("-", ""));
        Double dpmLng = 1 / mpdLng;
        Double radiusLng = dpmLng * raidusMile;
        //获取最小经度
        Double minLat = longitude - radiusLng;
        // 获取最大经度
        Double maxLat = longitude + radiusLng;
          
        Double dpmLat = 1 / degree;
        Double radiusLat = dpmLat * raidusMile;
        // 获取最小纬度
        Double minLng = latitude - radiusLat;
        // 获取最大纬度
        Double maxLng = latitude + radiusLat;
          
        map.put("minLat", minLat+"");
        map.put("maxLat", maxLat+"");
        map.put("minLng", minLng+"");
        map.put("maxLng", maxLng+"");
          
        return map;
    }
      
    public static void main(String[] args) {
        //测试经纬度：117.11811  36.68484
        //测试经纬度2：117.00999000000002  36.66123
        //System.out.println(getDistance("117.11811","36.68484","117.00999000000002","36.66123"));
          
        System.out.println(getAround("117.11811", "36.68484", "13000"));
        //117.01028712333508(Double), 117.22593287666493(Double),
        //36.44829619896034(Double), 36.92138380103966(Double)
          
    }
      
}

算法数学上实现思路: 判断一个点是在一个多边形内部的集中情况
第一:目标点在多边形的某一个顶点上,我们认为目标点在多边形内部
第二:目标点在多边形的任意一天边上,我们认为目标点在多边形内部
第三:这种情况就比较复杂了,不在某天边上，也不和任何一个顶点重合.这时候就需要我们自己去算了，解决方案是将目标点的Y坐标与多边形的每一个点进行比较，我们会得到一个目标点所在的行与多边形边的交点的列表。如果目标点的两边点的个数都是奇数个则该目标点在多边形内，否则在多边形外。

这种算法适合凸多边形也适合凹多边形，所以是一种通用的算法，同时也解决了多边形的点的顺序不同导致的形状不同，比如一个五边形，可以是凸五边形，也可以是一个凹五边形，这个根据点的位置和顺序决定的。

有了数学上的实现思路，辣么我们就可以用java 或者去他语言去实现一个点(经纬度)是否在一个多边形内部了(多个点构成)。

我们先写一个 对点和线的一些公用方法，

package cn.liuzw.point;
import java.util.ArrayList;
 
/**
 *  点和线的一些公用方法

 * 
 * @author liuZhiwei
 * 2016年8月6日 下午3:48:38
 */
public class Point {
	
	/**
	 *  是否有 横断

	 *  参数为四个点的坐标
	 * @param px1
	 * @param py1
	 * @param px2
	 * @param py2
	 * @param px3
	 * @param py3
	 * @param px4
	 * @param py4
	 * @return  
	 */
	public boolean isIntersect ( double px1 , double py1 , double px2 , double py2 , double px3 , double py3 , double px4 ,  
			double py4 )  
	{  
		boolean flag = false;  
		double d = (px2 - px1) * (py4 - py3) - (py2 - py1) * (px4 - px3);  
		if ( d != 0 )  
		{  
			double r = ((py1 - py3) * (px4 - px3) - (px1 - px3) * (py4 - py3)) / d;  
			double s = ((py1 - py3) * (px2 - px1) - (px1 - px3) * (py2 - py1)) / d;  
			if ( (r >= 0) && (r <= 1) && (s >= 0) && (s <= 1) )  
			{  
				flag = true;  
			}  
		}  
		return flag;  
	} 
	/**
	 *  目标点是否在目标边上边上

	 *  
	 * @param px0 目标点的经度坐标
	 * @param py0 目标点的纬度坐标
	 * @param px1 目标线的起点(终点)经度坐标
	 * @param py1 目标线的起点(终点)纬度坐标
	 * @param px2 目标线的终点(起点)经度坐标
	 * @param py2 目标线的终点(起点)纬度坐标
	 * @return
	 */
	public boolean isPointOnLine ( double px0 , double py0 , double px1 , double py1 , double px2 , double py2 )  
	{  
		boolean flag = false;  
		double ESP = 1e-9;//无限小的正数
		if ( (Math.abs(Multiply(px0, py0, px1, py1, px2, py2)) < ESP) && ((px0 - px1) * (px0 - px2) <= 0)  
				&& ((py0 - py1) * (py0 - py2) <= 0) )  
		{  
			flag = true;  
		}  
		return flag;  
	} 
	public double Multiply ( double px0 , double py0 , double px1 , double py1 , double px2 , double py2 )  
	{  
		return ((px1 - px0) * (py2 - py0) - (px2 - px0) * (py1 - py0));  
	}
	/**
	 * 判断目标点是否在多边形内(由多个点组成)

	 * 
	 * @param px 目标点的经度坐标
	 * @param py 目标点的纬度坐标
	 * @param polygonXA 多边形的经度坐标集合
	 * @param polygonYA 多边形的纬度坐标集合
	 * @return
	 */
	public boolean isPointInPolygon ( double px , double py , ArrayList polygonXA , ArrayList polygonYA )  
	{  
		boolean isInside = false;  
		double ESP = 1e-9;  
		int count = 0;  
		double linePoint1x;  
		double linePoint1y;  
		double linePoint2x = 180;  
		double linePoint2y;  
 
		linePoint1x = px;  
		linePoint1y = py;  
		linePoint2y = py;  
 
		for (int i = 0; i < polygonXA.size() - 1; i++)  
		{  
			double cx1 = polygonXA.get(i);  
			double cy1 = polygonYA.get(i);  
			double cx2 = polygonXA.get(i + 1);  
			double cy2 = polygonYA.get(i + 1); 
			//如果目标点在任何一条线上
			if ( isPointOnLine(px, py, cx1, cy1, cx2, cy2) )  
			{  
				return true;  
			}
			//如果线段的长度无限小(趋于零)那么这两点实际是重合的，不足以构成一条线段
			if ( Math.abs(cy2 - cy1) < ESP )  
			{  
				continue;  
			}  
			//第一个点是否在以目标点为基础衍生的平行纬度线
			if ( isPointOnLine(cx1, cy1, linePoint1x, linePoint1y, linePoint2x, linePoint2y) )  
			{  
				//第二个点在第一个的下方,靠近赤道纬度为零(最小纬度)
				if ( cy1 > cy2 )  
					count++;  
			}
			//第二个点是否在以目标点为基础衍生的平行纬度线
			else if ( isPointOnLine(cx2, cy2, linePoint1x, linePoint1y, linePoint2x, linePoint2y) )  
			{  
				//第二个点在第一个的上方,靠近极点(南极或北极)纬度为90(最大纬度)
				if ( cy2 > cy1 )  
					count++;  
			}
			//由两点组成的线段是否和以目标点为基础衍生的平行纬度线相交
			else if ( isIntersect(cx1, cy1, cx2, cy2, linePoint1x, linePoint1y, linePoint2x, linePoint2y) )  
			{  
				count++;  
			}  
		}  
		if ( count % 2 == 1 )  
		{  
			isInside = true;  
		}  
 
		return isInside;  
	}  
}

现在通常都是接口实现 需要考虑到数据库和效率 通常都是mysql  数据量也大 如何去实现就各位自行发展吧