自然语言处理——句子的相似度

引言

句子的相似度有非常广泛的应用，比如文本搜索、问答系统等。今天我们来看下如何计算两个句子之间的相似度。

欧氏距离

我们可以通过计算两个句子之间的欧式距离来判断句子之间的相似度。距离越小则相似度越大。

欧式距离公式为：
$$d(X,Y)=|X-Y|=\sqrt{\sum _{i=1}^n(X_i-Y_i{)}^2}$$

即两个向量对应元素只差的平方和。

$d$就是两个句子的距离，$X$和$Y$是两个句子的向量。

$S_1$：“我们/今天/去/爬山” = (1,0,1,1,0,0,0,0)
$S_2$：“你们/昨天/跑步” = (0,0,0,0,0,1,1,1)
$S_3$：“你们/又/去/爬山/又/去/跑步” = (0,2,2,1,0,1,0,1)

在上篇文章中我们已经得到这样的句子表示。

那如何计算它们之间的距离呢，比如我们要计算$S_1$和$S_2$的距离。

$d(S_1,S_2)=\sqrt{1^2+0^2+1^2+1^2+0^2+1^2+1^2+1^2}=\sqrt{6}$
$d(S_1,S_3)=\sqrt{1^2+2^2+1^2+0^2+0^2+1^2+0^2+1^2}=\sqrt{8}$
$d(S_2,S_3)=\sqrt{0^2+2^2+2^2+1^2+0^2+0^2+1^2+0^2}=\sqrt{10}$

从上面的计算，我们可以看出来，$S_1$和$S_2$是最相似的。

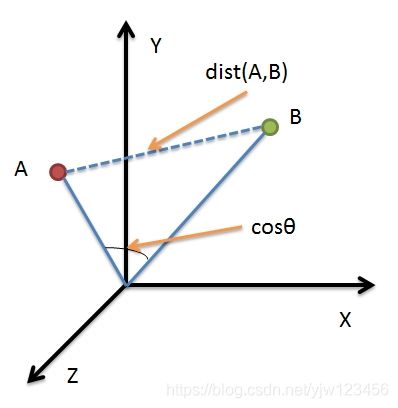
我们知道，向量是有方向的，但是欧式距离没有考虑向量的方向。我们下面看的方法可以同时考虑向量的大小和方向。

余弦相似度

余弦相似度公式为：
$$d(X,Y)=\frac{X\cdot Y}{||X||\times ||Y||}=\frac{{\sum }_{i=1}^n{X}_i\times Y_i}{\sqrt{{\sum }_{i=1}^n{X}_i^2}\times \sqrt{{\sum }_{i=1}^n{Y}_i^2}}$$

就是两个向量的内积除以两个向量模的乘积。计算出来的值越大，则相似度越大。

余弦相似度和欧式距离的区别见上图。

$S_1$：“我们/今天/去/爬山” = (1,0,1,1,0,0,0,0)
$S_2$：“你们/昨天/跑步” = (0,0,0,0,0,1,1,1)
$S_3$：“你们/又/去/爬山/又/去/跑步” = (0,2,2,1,0,1,0,1)
下面计算它们之间的余弦相似度：
$d(S_1,S_2)=0/?=0$因为$S_1\cdot S_2=0$，所以它们的余弦相似度就是0，分母不需要计算了。
$d(S_1,S_3)=\frac{0+0+2+1+0+0+0+0}{\sqrt{1+1+1}\times \sqrt{2^2+2^2+1+1+1}}=\frac{3}{\sqrt{33}}$
$d(S_2,S_3)=\frac{0+0+0+0+0+1+0+1}{\sqrt{1+1+1}\times \sqrt{2^2+2^2+1+1+1}}=\frac{2}{\sqrt{33}}$

从中我们可以得到，句子$S_1$和$S_3$的相似度是最大的。

和欧式距离计算的结果不同，但是我们看两个句子的话，可以感觉得到这里余弦相似度计算的结果更加正确。

参考

1. 贪心学院课程
2. https://www.it610.com/article/3203002.htm