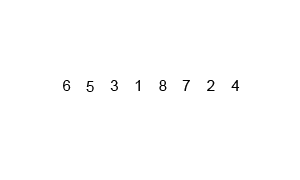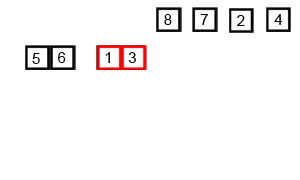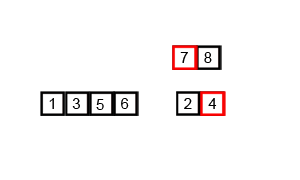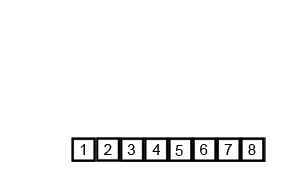【十大排序】带你深入了解归并排序

☞梦想进大厂的一只程序猿☜
☞期望毕业前力扣刷够400题☜
☞正在复习数据结构和算法☜
☞博客地址：https://www.huangliangshuai.com/☜

【2020秋招-面试题目汇总（随时更新）】

排序系列传递门

• 堆排序
• 快速排序
• 归并排序
• 希尔排序
• 插入排序
• 冒泡排序

1. 了解

归并排序，是创建在归并操作上的一种有效的排序算法。算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。归并排序思路简单，速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列。
一般求逆序对时，使用！！！

2. 图解

归并的精髓在于：分而治之

3. 代码分析

1. 通过上面的图解，我们可以看到，归并排序是将一个数组拆分至一个，在利用Merge(归并)的思想，变成2个、4个、8个等
2. 我们来想想，具体的代码应该怎么实现?
3. 考虑当数组为0或1时的操作

public int reversePairs(int[] nums) {
		int len = nums.length;
		if (len < 2) {
			return 0; // 如果长度为1或者是0的话，则直接返回0
		}
		int[] temp = new int[len]; // 利用这个辅助数组来进行交换

		int[] copy = new int[len]; // 我们存储一个原来的数组，这样容易看出比较性

		for (int i = 0; i < len; i++) {
			copy[i] = nums[i];
		}
		// 这里我们的边界是[0,len-1],辅助数组为temp
		return reversePairs(copy, 0, len - 1, temp);
	}

4. 我们怎么才能把一个数组分成一块一块，然后再合并呢？
   用到了递归的思想，我们想一想，终止条件是什么：当只剩下一个时，终止，也就是left == right,
   我们对左边进行reversePairs、对右边进行reversePairs，得到两个有序的数组
   对他们进行mergeAndCount，计算逆序对的值

public int reversePairs(int[] nums, int left, int right, int[] temp) {
		if (left == right) {
			return 0;
		}
		int mid = left + (right - left) / 2;
		int leftPairs = reversePairs(nums, left, mid, temp);
		int rightPairs = reversePairs(nums, mid + 1, right, temp);

		int crossPairs = mergeAndCount(nums, left, mid, right, temp);
		return leftPairs + rightPairs + crossPairs;
	}

5. 再进行mergeAndCount，我们就要实现，两个有序的数组，怎么变成一个数组：双指针、依次比较即可
   这里注意两个地方：
   第一个是边界的处理，当i == mid + 1 或者 j == right + 1
   第二个是count（逆序对的处理)
   
   我们可以看到，5的值是大于4的，也就是5和7都是符合逆序对的，我们观察可以看出，逆序对的数量也就是左边数组剩余的个数：mid - i + 1

public int mergeAndCount(int[] nums, int left, int mid, int right, int[] temp) {
		for (int i = left; i <= right; i++) {
			temp[i] = nums[i];
		}
		int i = left;
		int j = mid + 1;
		int count = 0;
		for (int k = left; k <= right; k++) {
			if (i == mid + 1) {
				nums[k] = temp[i];
				i++;
			} else if (j == right + 1) {
				nums[k] = temp[j];
				j++;
			} else if (temp[i] <= temp[j]) {
				nums[k] = temp[i];
				i++;
			} else if (temp[i] > temp[j]) {
				nums[k] = temp[j];
				j++;
				count += mid - i + 1;
			}
		}
		return count;
	}

6. 最后，我们得到这个逆序对的数值，我们来提交一下，看看可不可以通过~
   
   成功通过~~~

4.题目代码

// 手撕归并 -- 逆序对
public class Demo01 {
	public int reversePairs(int[] nums) {
		int len = nums.length;
		if (len < 2) {
			return 0; // 如果长度为1或者是0的话，则直接返回0
		}
		int[] temp = new int[len]; // 利用这个辅助数组来进行交换

		int[] copy = new int[len]; // 我们存储一个原来的数组，这样容易看出比较性

		for (int i = 0; i < len; i++) {
			copy[i] = nums[i];
		}
		// 这里我们的边界是[0,len-1],辅助数组为temp
		return reversePairs(nums, 0, len - 1, temp);
	}

	public int reversePairs(int[] nums, int left, int right, int[] temp) {
		if (left == right) {
			return 0;
		}
		int mid = left + (right - left) / 2;
		int leftPairs = reversePairs(nums, left, mid, temp);
		int rightPairs = reversePairs(nums, mid + 1, right, temp);

		int crossPairs = mergeAndCount(nums, left, mid, right, temp);
		return leftPairs + rightPairs + crossPairs;
	}

	public int mergeAndCount(int[] nums, int left, int mid, int right, int[] temp) {
		for (int i = 0; i < nums.length; i++) {
			temp[i] = nums[i];
		}
		int i = left;
		int j = mid + 1;
		int count = 0;
		for (int k = left; k <= right; k++) {
			if (i == mid + 1) {
				nums[k] = temp[i];
				i++;
			} else if (j == right + 1) {
				nums[k] = temp[j];
				j++;
			} else if (temp[i] <= temp[j]) {
				nums[k] = temp[i];
				i++;
			} else if (temp[i] > temp[j]) {
				nums[k] = temp[j];
				j++;
				count += mid - i + 1;
			}
		}
		return count;
	}
}