树的例子
我们已经学过了像栈和队列这样的线性数据结构,同时我们对递归也有了一定的了解,现在让我们来看看另一种常见的数据结构——树(Tree)。树在计算机科学里应用广泛,包括操作系统,图形学,数据库和计算机网络。树和真正的树有许多相似的地方,也包括根、树枝和叶子,它们的不同在于计算机中的树的根在顶层而它的叶子在底部。
在我们开始学习树之前,让我们先来看看几个常见的关于树的例子。首先让我们看看生物学中的分类。图 1 是一个动物分类的例子,从中我们可以看出树的几个特点。第一,这个例子说明树是分级的,这里分级的意思是树的顶层部分更加宽泛,而底部更加具体。在这个例子中,最上层的是“界”,它下面的一层(上层的子级)是“门”,然后是“纲”等等。但是,无论我们细分到多少层,这里面包含的生命体也都是动物。
图 1:一些动物的分类树
我们注意到可以从树的顶层开始然后沿着圆圈和箭头构成的一条路径到达树的底层。在树的每一层我们都可以问自己一个问题,然后沿着相符的那条路径继续下去。比如我们可以问 “这个动物是脊椎动物还是无脊椎动物”,如果回答是“脊椎动物”我们就沿着脊椎动物这条路下去然后接着问“这个脊椎动物是哺乳动物吗”,如果回答“不是哺乳动物”我们就卡在这里了(不过仅限于这个简单的例子会有这种情况)。当我们到达哺乳动物这一层的时候我们问自己“这个哺乳动物是灵长类还是食肉动物”。我们可以沿着路径一直走下去直到树的最底层,这也就能看到动物的名称了。
树的第二个特点是一个节点(node)的所有子节点(children)和另一个节点的子节点是完全独立的。比如“猫属”有两个子节点“家生”和“野生”,“蝇属”中也有一个“家生”,但它和“猫属”中的“家生”完全不同而且相互独立。这意味着我们可以在不影响“猫属” 的子节点的情况下更改“蝇属”的子节点。
树的第三个特点就是每个它的叶节点(leaf)都是不同的。对每一种动物,我们都可以从根节点(root)开始沿着一条特定的路径找到它对应的叶节点,并把它和其他动物区分开,例如对于家猫,我们可以沿着动物界——脊索动物门——哺乳动物纲——食肉动物目——猫科——猫属——家猫找到它。
另一个树的例子就是你每天都会用到的文件系统。在文件系统中,磁盘的分支或者说子目录都是运用了树来构建的。图 2 展示了Unix文件系统的部分的分层情况。
图 2 :Unix文件系统的部分的分层情况
这个树的文件系统和真正的树也非常相像。你可以从根节点出发沿着一条路径到任意分支。这条路径会把这个子分支(包括它里面的所有文件)和其他分支区别开。树的另一重要特点,就是你可以将树下层的所有部分(叫做子树subtree)移动到树的另一位置而不影响更下层的情况,这是由树的分级方式决定的。例如,我们可以将所有标注/etc的子树从根节点下移动到usr/下面。这样做会将 httpd 的路径从/etc/httpd改变成/usr/etc/httpd,但是对httpd的内容和子节点的内容不会有影响。
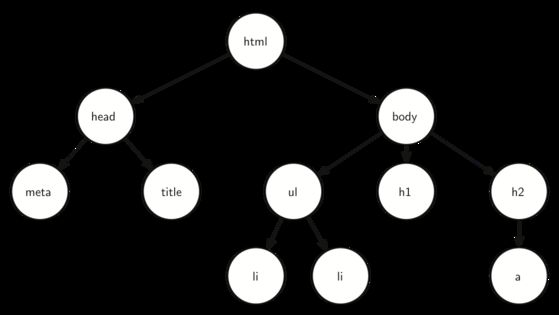
最后一个树的例子是一个网页。下图是一个利用超文本标记语言(HTML)编写的简单网页。图 3 是构成网页的超文本标记语言中的标签相互关联关系所构成的树。
simple
A simple web page
- List item one
- List item two
Luther CS
图 3 :网页的标记符之间的相互关联所构成的树
上面的超文本标记的代码和它对应的树说明了另一种分级方式。我们发现树的每一层都对应超文本标记符的一层嵌套。代码的第一个标记符是同时最后一个是。这一页中所有其他的标记符也都是成对的。试一下你就会发现这种嵌套的特点在树的每一层都是成立的。
术语表与定义
现在我们已经看了几个树的例子了,现在正式定义树以及构成它的要素。
节点(Node)
节点是树的基本构成部分。它可能有其他专属的名称,我们称之为“键(key)”。一个节点也可能有更多的信息,我们称之为“负载”。虽然负载信息和树的许多算法并不直接相关,但是它对于树的应用至关重要。
边(Edge)
边也是树的基本构成部分。边连接两个节点,并表示它们之间存在联系。除了根节点外每个节点都有且只有一条与其他节点相连的入边(指向该节点的边),每个节点可能有许多条出边(从该节点指向其他节点的边)。
根节点(Root)
根节点是树种中唯一一个没有入边的节点。在图 2 中,“/”是树的根节点。
路径(Path)
路径是由边连接起来的节点的有序排列。例如:(动物界——脊索动物门——哺乳动物纲——食肉动物目——猫科——猫属——家猫)就是一条路径。
子节点集(Children)
当一个节点的入边来自另一个节点时,我们称前者是后者的子节点,同一个节点的所有子节点构成子节点集。在图 2 中,节点log/,spool/,yp/构成节点var/的子节点集。
父节点(Parent)
一个节点是它出边所连接的所有节点的父节点。在图 2 中,节点var/是节点log/,spool/,yp/的父节点。
兄弟节点(Sibling)
同一个节点的所有子节点互为兄弟节点,在文件系统树中节点etc/和节点usr/是兄弟节点。
子树(Subtree)
子树是一个父节点的某个子节点的所有边和后代节点所构成的集合。
叶节点(Leaf Node)
没有子节点的节点成为称为叶节点。例如图 1 中的“人”和“黑猩猩”就是叶节点。
层数(Level)
一个节点的层数是指从根节点到该节点的路径中的边的数目。例如,图 1 中“猫属”的层数是 5,定义根节点的层数为 0。
高度(Height)
树的高度等于所有节点的层数的最大值。图 2 中树的高度为 2。
我们已经定义好所需的术语了,现在可以正式定义树了。我们将用两种方式定义,一种需要用到节点和边,而另一种更为有效的定义方式是利用递归定义。
定义一:树是节点和连接节点的边的集合,它有以下特征:
有一个节点被设计为根节点。
除了根节点的每一个节点 n,都通过一条边与它唯一的父节点相连。
可以沿着唯一的路径从根节点到每个节点。
如果这个树的每个节点都至多有两个子节点,我们称它为二叉树。
图 4 展示了一个符合定义一的树。每条边的箭头指出了连接的方向。
图 4 :由节点和边构成的树
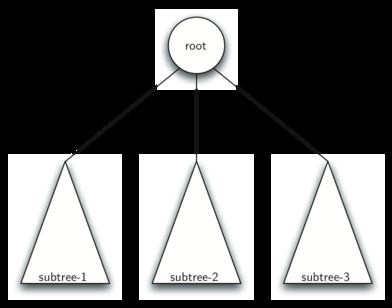
定义二:每个树或者为空,或者包含一个根节点和 0 个或多个子树,其中每个子树也符合这样的定义。每个子树的根节点和其父树的根节点之间通过边相连。图 5 描绘了这种递归定义的树。通过这种树的递归定义,我们知道图 5 中的树至少有 4 个节点,因为每个三角形所代表的子树必须有根。它也可能有更多的节点,但我们需要更深入的了解这棵树来得到答案。
图 5 :递归法定义的树