Local Outlier Factor 算法（以Boxplot探测LOF离群值）及python手写（非sklearn）

local outliers “本地离群值”，能够在基于密度不同的数据分布下（如下图），探测出各个不同密度集群边缘的离群值。LOF是基于密度的离群值探测算法，通过计算样本的local outlier factor（翻译过来应该是本地离群值因子）以判断该样本是否为离群值。

LOF四部曲

1. k-distance
   设定一个整数 k 和一个点 o ，点 o 的k-distance为 k-distance(o) = ɛ
   N_k(o) 为点o的 ɛ-近邻的个数，N_k(o)为整数，通常N_k(o)就等于k
   ɛ 是点 o 与第 k 个最近邻的距离
   例子：
   N₁(a) = {b} = 1, k-distance(a) = dist(b,a);
   N₂(a) = {b,c} =2, k-distance(a) = dist(c,a);
   

2. reachability distance
   点 p 的reachability distance 基于：
   给定2个点 p 和 o 和一个整数 k
   reach_dist_k(p, o) 等于 max{dist(p,o), k-distance(o)}
   
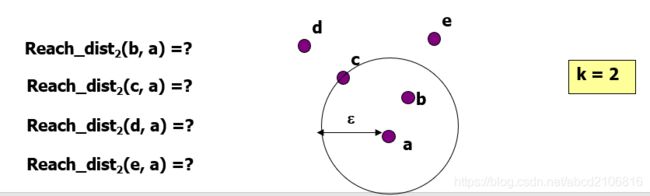
   reach_dist₂(b, a) = dist(c, a)
   reach_dist₂(c, a) = dist(c, a)
   reach_dist₂(d, a) = dist(d, a)
   reach_dist₂(e, a) = dist(e, a)

3. Average reachability distance
   

4. Local reachability dencity
   

5. Local outlier factor
   

最后得出一组数即为所有样本的LOF值，有说法是LOF值大于1的即为本地离群值，但通过实验证明此说法不严谨，但可以确定的是LOF值越大其为离群值的概率就越大，因此本文用Boxplot分箱法探测样本LOF值的离群值，定义LOF值的离群值为本地离群值。

以下为本文代码（此结果与sklearn计算结果一致，复杂代码后都有注释，附图）

import numpy as np
class LOF():
    def __init__(self, data, k, a=2):
        self.data = data
        self.k = k
        self.a = a

    def adaption(self):
        '''
        先判定k值是否小于数据长度，再判定数据类型是否符合
        '''
        #import numpy as np
        arr = self.data
        if self.k > len(self.data):
            raise KeyError('The value of K is larger than the length of array')
        if 'DataFrame' in str(type(self.data)):
            try:
                import pandas as pd
                arr = self.data.values
            except:
                raise ModuleNotFoundError('Either change your data type to numpy.ndarray or install Pandas')
        elif type(self.data) is list:
            arr = np.array(self.data)
        return arr

    def dist_table(self):
        '''
        利用numpy的向量范数计算各点间的距离，a系数及ord=1即曼哈顿距离，=2即欧几里得距离，np.inf(正无穷)即闵可夫斯基距离
        '''
        #import numpy as np
        arr = self.adaption()
        dc = np.zeros(shape=(arr.shape[0], arr.shape[0]))
        for i in range(len(arr)):
            temp = []
            for j in range(len(arr)):
                dis = np.linalg.norm(arr[i,:]-arr[j,:], ord=self.a)
                temp.append(dis)
            temp = np.array(temp)
            dc[:,i] = temp
        return dc

    def kdist(self):
        '''
        The distance between o and the k-th nearest neighbor
        '''
        #import numpy as np
        dt = self.dist_table()
        kd = []
        nn = {}   #k个最邻点index
        for i in range(len(dt)):
            dl = dt[:,i].tolist()
            mindist = sorted(dl,reverse=False)[1:self.k+1]
            kd.append(max(mindist))
            index = []
            for m in mindist:
                idx = [y for y, x in enumerate(dl) if x == m]#找该距离对应值的索引
                for j in idx:
                    if j not in index and j != i:         #不添加重复的index,且不添加与自己相同的索引
                        index.append(j)
                        break
            nn[i] = index
        return kd, nn, dt
    

    def rbdist(self):
        '''
        设Reach_distk(i, j)，i为行，j为列
        Reach_distk(i, j) = max{dist(i, j), k-distance(j)}
        '''
        #import numpy as np
        kd, nn, dt = self.kdist()
        rd = np.zeros(shape=(dt.shape[0], dt.shape[1]))
        for i in range(len(rd)):
            for j in nn[i]:
                rd[i,j] = max([dt[i,j]] + [kd[j]])
        return rd


    def lrd(self):
        '''
        Local Reachability Density
        Nk(P) / ∑Nk(P)Reach_distk(i, j)
        '''
        #import numpy as np
        rd = self.rbdist()
        lrd_ls = []
        for i in range(len(rd)):
            rs = rd[i].sum()
            if rs == 0:     #设有k+1个以上的点在同一个坐标，则他们的rbdist=0，这种情况令其=k/0.1
                lrd_ls.append(self.k / 0.1)
            else:
                lrd_ls.append(self.k / rs)
        return lrd_ls


    def lof(self):
        '''
        ∑Nk(P)(lrd(o)/lrd(p)) / |Nk(P)|
        '''
        #import numpy as np
        ld = self.lrd()
        _, nn, _ = self.kdist()
        lof_ls = []
        for i in range(len(ld)):
            sum_lrd_o = 0
            for j in range(self.k):
                sum_lrd_o += ld[nn[i][j]]
            if sum_lrd_o == 0 and ld[i] == 0:  #设两者都为0(不存在只有ld[i]=0的情况)时，除法等于0.1/k
                lof_ls.append(0.1 / self.k)
            else:
                lof_ls.append((sum_lrd_o / ld[i]) / self.k)
        return np.array(lof_ls).reshape(-1,1)

    def pred(self):
        '''
        Boxplot method to detect the 1-dimentional LOF outliers
        '''
        lof_result = self.lof()
        q1 = np.quantile(lof_result,0.25,interpolation='lower')
        q3 = np.quantile(lof_result,0.75,interpolation='higher')
        iqr = q3-q1
        up_outliers = 1.5*iqr + q3
        lof_result = np.where(lof_result > up_outliers, -1, 1)
        return lof_result



import matplotlib.pyplot as plt
np.random.seed(42)

# Generate train data
X_inliers = 0.3 * np.random.randn(100, 2)
X_inliers = np.r_[X_inliers + 2, X_inliers - 2]

# Generate some outliers
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.r_[X_inliers, X_outliers]
n_outliers = len(X_outliers)
ground_truth = np.ones(len(X), dtype=int)
ground_truth[-n_outliers:] = -1

#计算lof
lof = LOF(X, 20).lof()
y_pred = LOF(X, 20).pred()

#绘图
pred_normal = X[np.where(y_pred==1)[0]]
pred_outliers = X[np.where(y_pred==-1)[0]]
lof_outliers = lof[np.where(y_pred==-1)[0]]

#数据分布原图
plt.figure(figsize=(8,6))
plt.scatter(X[:,0], X[:,1], marker='.')
plt.title('Original Distribution', fontsize=20)
plt.show

#lof算法处理后
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111)
ax.scatter(pred_normal[:,0], pred_normal[:,1], marker='.', label='Normal Points')
ax.scatter(pred_outliers[:,0], pred_outliers[:,1], marker='.', label='Outliers')
ax.legend()
ax.set_title('Local Outlier Factor', fontsize=20)
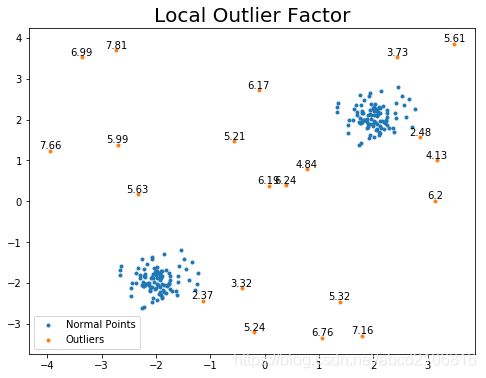
for i in range(len(lof_outliers)):  
    plt.text(pred_outliers[i,0], pred_outliers[i,1], round(lof_outliers[i][0],2), ha='center', va='bottom', fontsize=10)  

可视化结果

(原分布图)

（手写LOF探测图）

（sklearn探测）

（手写LOF值与sklearn的对比）
由图可见lof值是完全相同的，不同在于离群值的预测上，本文采用Boxplot分箱法对计算出的LOF值进行离群值探测，在Boxplot探测出来的离群值即判定为原数据集的离群值。因此跟sklearn上的预测略有不同，也不知sklearn是如何判定离群值，官方文档也好像没有提到这一点，不过还是可以对比一下结果看下哪个更精确。
虽然离群值判定上略有不同，但是预测的LOF值是完全一样。

from sklearn.neighbors import LocalOutlierFactor
clf = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
# use fit_predict to compute the predicted labels of the training samples
# (when LOF is used for outlier detection, the estimator has no predict,
# decision_function and score_samples methods).
y_pred_s = clf.fit_predict(X)
n_errors = (y_pred != ground_truth).sum()
X_scores = clf.negative_outlier_factor_
#绘图（变量名与上面手写LOF绘图代码一样，可以加以修改）
pred_normal = X[np.where(y_pred_s==1)[0]]
pred_outliers = X[np.where(y_pred_s==-1)[0]]
lof_outliers = X_scores[np.where(y_pred_s==-1)[0]]

fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111)
ax.scatter(pred_normal[:,0], pred_normal[:,1], marker='.', label='Normal Points')
ax.scatter(pred_outliers[:,0], pred_outliers[:,1], marker='.', label='Outliers')
ax.legend()
ax.set_title('Local Outlier Factor', fontsize=20)
for i in range(len(lof_outliers)):  
    plt.text(pred_outliers[i,0], pred_outliers[i,1], round(lof_outliers[i],2), ha='center', va='bottom', fontsize=10)  


#判断手写LOF与sklearn的lof是否相同
b = np.around(lof.reshape(1,-1)[0], decimals=3) #手写的LOF值，调整格式
a = np.around(X_scores*-1, decimals=3) #sklearn出的LOF值，调整格式
a.tolist() == b.tolist() #转换成list来判断