最小生成树——Kruskal的应用和证明

（不知道为什么最近沉迷于基础算法中......）

既然复习了好久基础算法和基本数据结构，最近就学习了一下最小生成树算法（本人蒟蒻）

最小生成树是个虾米东西呢？

首先无毋庸置疑的，最小生成树一定是一课树（废话.......）

那树是什么呢？

这是一棵树

好吧，其实树就是一个无向连通图，其中n个结点n-1条边，且图中不存在环

那最小生成树就是在一张无向连通带权图中由n个结点所构成的一棵权值之和最小的一棵树

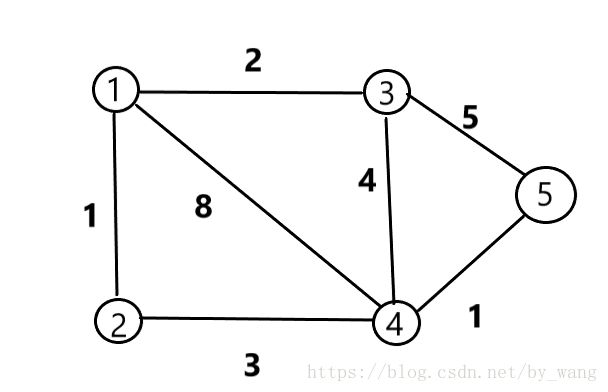
例子如下图

这张图的最小生成树包含了

结点1-2的边权为1的边

结点4-5的边权为1的边

结点1-3的边权为2的边

结点2-4的边权为3的边

于是这张图的最小生成树就这样出现了。。。

那么我们如何去解决这个问题呢？

下面给出一种常见的算法Kruskal（prim的堆优化还没想好，下次补上QAQ）

思路，个人感觉比较简单。

Kruskal是根据边来解决问题的，首先对于所有的边我们记录它两端的点和它的权值

之后以边上的权重为第一关键字进行从小到大的排序

将边依次加入最小生产树，这时我们会发现一个重大的问题

随意的将边加入最小生成树中很容易让树中形成环（话说这样就变成基环树了）

怎么办？

所以每当我们加入一条边的时候，应该判断是否构成环

ennnnnn，玄学级的超快数据结构出现了——并查集（下次再说）

通过并查集常数级别的时间复杂度加持来判断加入边两端所在的集合是否为同一个，来判断环的问题

于是Kruskal的时间复杂度就这样出现了O(mlgm)（都是排序的慢，m为边的数量）

问题又来了，为什么这个算法是正确的嘞？

要证明Kruskal算法生成的是最小生成树，我们分两步来证明：

（1）Kruskal算法一定能得到一个生成树；

（2）该生成树具有最小代价。

证明如下：

（1）假设该算法得到的不是生成树，根据树的定义，就有两种情形，第一是得到的图是有环的，第二就是得到的图是不连通的。由于算法要求每次加入边都是无环的，所以第一种情形不存在，下面就只需证明第二种情形不存在即可。

假设得到的图是不连通的，则至少包含两个独立的的边集，假设其中一个为E，则E中边对应的所有点都无法到达其它边集对应的点（否则，根据算法定义，相应的联系边应被加入树中），而这与原图是连通的产生矛盾，因此，第二种情形也不可能存在。得证。

（2）假设图有n个顶点，则生成树一定具有n-1条边.由于图的生成树个数是有限的，所以至少有一棵树具有最小代价，假设该树为U。先做出如下假设：

1)得到的树为T。

2)U和T中不同的边的条数为k,其它n-1-k条边相同，这n-1-k条边构成边集E。；

3)在T中而不在U中的边按代价从小到大依次为a1，a2，...，ak。

4)在U中而不在T中的边按代价从小到大依次为x1，x2，...，xk。

现在我们通过把U转换为T（把T的边依次移入U中），来证明U和T具有相同代价。

首先，我们将a1移入U中，由于U本身是一棵树，此时任意加一条边都构成回路，所以a1的加入必然产生一条回路，且这条回路必然包括x1，x2，...，xk中的边。（否则a1与E中的边构成回路，而E也在T中，这与T中无回路矛盾。）

在这个回路中删除属于x1，x2，...，xk且代价最大边xi构成一个新的生成树V。

假设a1代价小于xi，则V的代价小于U，这与U是最小代价树矛盾，所以a1不可能小于xi。

假设a1大于xi，按照Kruskal算法，首先考虑代价小的边，则执行Kruskal算法时，xi应该是在a1之前考虑，而a1又在a2，...，ak之前考虑，所以考虑xi之前，T中的边只能是E中的边，而xi既然没加入树T，就说明xi必然与E中的某些边构成回路，但xi和E又同时在U中，这与U是生成树矛盾，所以a1也不可能大于xi。

因此，新得到的树V与T具有相同代价。

依次类推，把a1，a2，...，ak的边逐渐加到U中，最终得到的树（T)与U代价相同。

证明结束。（好吧，以上是我抄的）

最后贴上一发代码（格式丑勿喷)（还有并查集我没写按质合并）

var
n,m,i,l,ans,rootx,rooty:longint;
pre,u,v,weight:array[1..200100] of longint;
bb:boolean;
procedure sort(l,r: longint);//快排不解释
var
i,j,x,y: longint;
begin
  i:=l; j:=r;
  x:=weight[(l+r) div 2];
  repeat
   while weight[i]    while x    if not(i>j) then
    begin
      y:=weight[i]; weight[i]:=weight[j]; weight[j]:=y;
      y:=u[i]; u[i]:=u[j]; u[j]:=y;
      y:=v[i]; v[i]:=v[j]; v[j]:=y; 
      inc(i); j:=j-1;
    end;
   until i>j;
   if l    if i end;
procedure dfsx(id:longint);//并查集找根
begin
  if pre[id]=id then begin rootx:=id; exit; end;
  dfsx(pre[id]);
  pre[id]:=rootx;//路径压缩
end;
procedure dfsy(id:longint);//同上
begin
  if pre[id]=id then begin rooty:=id; exit; end;
  dfsy(pre[id]);
  pre[id]:=rooty;
end;
procedure solve(x,y:longint);判断是否在一个集合内
begin
 dfsx(x); dfsy(y);
 if rootx=rooty then begin bb:=false; exit; end
 else begin pre[rooty]:=rootx; bb:=true; end;
end;
begin
  readln(n,m);
  for i:=1 to n do pre[i]:=i;
  for i:=1 to m do readln(u[i],v[i],weight[i]);
  sort(1,m);
  for i:=1 to m do
  begin
    bb:=false;
    solve(u[i],v[i]);
    if bb=true then begin inc(l); ans:=ans+weight[i]; end;
    if l=n-1 then break; 
  end;
  if l<>n-1 then begin writeln('orz'); halt; end;
  writeln(ans);
end.

以上就是Kruskal了

（话说谁知道网易公开课麻省理工的算导课的最小生成树，贪婪算法去哪里了）