画一个优美的树

我的目的是想画一个结构紧凑、没有冲突、节点分布均匀的树。例如
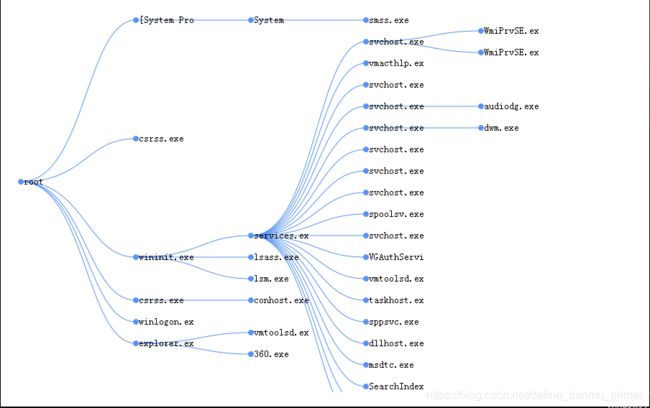
pymag-trees是一种画树算法的python实现。 这是这种算法的介绍和具体分析。

OGDF

OGDF，Open Graph Drawing Framework，是一个强大的，独立的c++类库，用于图表的自动布局。她不能直接画图但可以输出svg等格式的文件。

代码

用于布局的代码是我从ogdf中“截取的”，再加上一个树结构保存布局完成后的节点坐标及其它信息。得到坐标后就可以用各种gui框架画出来了，例如qt。

树结构

tree.hh

TreeChart

TreeChart.h

#pragma once

#include 
#include "tree.hh"

class STreeChart
{
	struct ProcessInfo
	{
		std::string strName;

		int nProcessId;
		int nParentId;

		double x;
		double y;
		double mod;
	};

	//! Determines the orientation in hierarchical layouts.
	enum class Orientation {
		topToBottom, //!< Edges are oriented from top to bottom.
		bottomToTop, //!< Edges are oriented from bottom to top.
		leftToRight, //!< Edges are oriented from left to right.
		rightToLeft  //!< Edges are oriented from right to left.
	};

	//! Determines how to select the root of the tree.
	enum class RootSelectionType {
		Source, //!< Select a source in the graph.
		Sink,   //!< Select a sink in the graph.
		ByCoord   //!< Use the coordinates, e.g., select the topmost node if orientation is topToBottom.
	};

public:
	STreeChart():m_siblingDistance(20),
		m_subtreeDistance(30),
		m_levelDistance(150),
		m_treeDistance(50),
		m_orthogonalLayout(false),
		m_orientation(Orientation::leftToRight)
	{
		m_nLeft = m_nRight = m_nBottom = m_nTop = 8;

		m_bDown = false;
		xMove = 0;
		yMove = 0;

		ProcessInfo info;
		info.strName = "root";
		root = m_Tree.set_head(info);

		//test graph
		for (int i = 0; i < 3; i++)
		{
			info.strName = str(boost::format("%d.exe") % i);
			tree::iterator node = m_Tree.append_child(root, info);

			if (i == 1)
			{
				continue;
			}

			if (i == 5)
			{
				for (int j = 0; j < 1; j++)
				{
					info.strName = str(boost::format("%d-%d.exe") % i % j);
					m_Tree.append_child(node, info);
				}
				continue;
			}

			for (int j = 0; j < 2; j++)
			{
				info.strName = str(boost::format("%d-%d.exe") % i % j);
				tree::iterator nodeNext = m_Tree.append_child(node, info);
				/*if (j == 1)
				{
					info.strName = "xxxx.exe";
					m_Tree.append_child(nodeNext, info);
				}*/
			}
		}
	}
	~STreeChart()
	{

	}

	void call();

private:
	struct TreeStructure;

	double m_siblingDistance;        //!< The minimal distance between siblings.
	double m_subtreeDistance;        //!< The minimal distance between subtrees.
	double m_levelDistance;          //!< The minimal distance between levels.
	double m_treeDistance;           //!< The minimal distance between trees.

	bool m_orthogonalLayout;         //!< Option for orthogonal style (yes/no).
	Orientation m_orientation;       //!< Option for orientation of tree layout.
	RootSelectionType m_selectRoot;  //!< Option for how to determine the root.

	void firstWalk(TreeStructure &ts, tree::iterator_base &subtree, bool upDown);
	void apportion(TreeStructure &ts, tree::iterator_base &subtree, tree::iterator_base &defaultAncestor, bool upDown);
	void secondWalkX(TreeStructure &ts, tree::iterator_base &subtree, double modifierSum);
	void secondWalkY(TreeStructure &ts, tree::iterator_base &subtree, double modifierSum);

	// compute y-coordinates and edge shapes
	void computeYCoordinates();
	void computeXCoordinates();

	int m_nLeft;
	int m_nTop;
	int m_nRight;
	int m_nBottom;

	tree m_Tree;
	tree::iterator root;

	bool m_bDown;

	int xMove;
	int yMove;


};

TreeChart.cpp

#include "pch.h"
#include "TreeChart.h"

#include 

其它

有需要的欢迎交流。