吴恩达直升机控制系列论文笔记

参考论文：

• Learning vehicular dynamics, with application to modeling helicopters.2005.nips。这篇论文在不知道直升机空气动力学模型的情况下，根据直升机的飞行数据，采用机器学习的方法学习到了直升机的运动模型。
• Autonomous helicopter flight via Reinforcement Learning.2004.nips。这篇论文讲述采用强化学习的方法，设计了一个神经网络的控制器，在定点飞行上具有比人类优秀飞行员更好的性能。
• Autonomous inverted helicopter flight via reinforcement learning.2004.nips。这篇论文根据人类飞行员的倒立飞行数据，设计了一个能让直升机倒立飞行的控制器。
• An Application of Reinforcement Learning to Aerobatic Helicopter Flight.2006.nips。根据上述学习到的模型、控制器，实现了直升机的特技飞行。

1 论文背景

 直升机具有高度的随机性、非线性、动态性和自主性，直升机飞行被普遍认为是一个具有挑战性的控制问题。人们对直升机的空气动力学模型知之甚少，我们很难从直升机的大小、尺寸计算出它的空气动力学模型。

2 学习直升机的运动学模型

2.1 模型假设

 设计一个控制器通常是先分析直升机的气动力模型，然后根据该模型设计出一个合适的控制器。这种方法得到的模型有一个致命的缺陷，比如在飞行仿真中飞机可以飞行的非常完美，但是现实中却可能会坠机。因为这种方法得到的模型和现实中存在差距，因此动力学模型的应该是直接从真实的数据中学习到的。
 假定状态集S包含位置(x,y,z)，方向( )，速度 ，角速度 等，这些数据都是相对于飞机机身的数据。比如位置信息是飞机相对于起始点的坐标，速度信息是飞机向前、右、下飞行的速度。动作集A包含4个变量，分别为：

• U1和U2：直升机纵向和横向的控制，可以控制飞机前倾使得飞机向前运动，横向拉杆控制飞机向左倾，使得飞机向左飞行。
• U3：尾桨的控制，可以用于直升机的偏航控制。
• U4：直升机的主电机上叶片攻角的控制，可以控制直升机升力的大小。

 目前行业的提出的一个标准模型是这样的，它是一个线性模型。

图1 CIFER模型

 其中G是重力加速度9.81m/s2，△t是时间间隔，这里是0.1s。自由变量Cx,y,z等是每个轴向的阻尼，D0,1,2,34和C1,2,3,4是输入对状态量的影响，这些系数都是需要通过机器学习的方法拟合得到的。
 上面的线性模型根据输入量和当前的状态量直接计算得到下一个时刻的状态量，这种线性的方法难以捕捉到惯性等非线性模型。比如惯性，当飞机前向飞行的时候突然转弯，由于惯性它会有一个侧滑，就是说它的机头的方向和运动的方向不一致。这是一种非线性的效应，因为它同时依赖于线速度和角速度。因此，作者提出了一个基于加速度的模型，这个模型预测出每个时刻的加速度和角加速度，根据加速度计算得到下一个时刻的速度和角速度，再积分得到位置信息和角度信息。加速度模型如下：

图2 加速度预测模型

 其中 是加速度矢量在x,y,z轴上的分量。C变量和D变量是需要从数据中学习到的变量。在较新的论文中，作者对加速度提出了优化：

图3 改进的加速度预测模型

 主要有2个改进，一是每一项都增加了一个高斯的随机噪声Wxyz等，高斯噪声的方差和采集到的飞机的数据是一样的。另一个是在Z轴方向上增加了额外的项，这是因为飞机在高速运动时带来的升力(论文中并分析新模型所带来效果的提升)。
在计算得到t+1时刻的速度信息和角速度信息的时候，由于t时刻和t+1时刻的机身坐标已经发生变化，因此需要做一个旋转校正，根据下面的公式计算得到t+1时刻的加速度和角速度：

图4 速度更新方程

 式子中的R是旋转矩阵，用于上一时刻坐标系到当前时刻坐标系的转换。 是机身坐标中的加速度。
 在根据数据训练模型的过程中，有不同的评价标准，目前有业界主流的CIFER(Comprehensive Identification from Frequency Responses，频率响应综合识别)方法，它最小化频率上的误差来得到模型的参数。还有One-Step误差，它最小化频域上下一步预测值和真实值之间的最小误差。还有Lagged误差，即延时误差，它累计一段时间内的预测值和实际值之间的误差，它的公式如下：

图5 长程评价函数

 式子中T是中预测时间，H为评价的时间窗口， 是根据时刻t预测得到的t+h时刻的状态， 是t+h时刻的真实值。

2.3 实验结果

 作者在2架飞机上验证了运动学模型，一架是XCell Tempest直升机，一架是Bergen Industrial Twin helicopter，如下图所示。分别得到了800秒的训练数据，540秒的测试数据；110秒的训练数据，110秒的测试数据。作者对原始的数据做了一个卡尔曼滤波，得到100Hz的数据，然后下采样得到10Hz的数据。作者根据模型和评价方法，组合比较了这几种模型：

• Linear-One-Step，采用线性模型，训练代价函数为时域上的一步误差；
• Linear-CIFER，采用线性模型，训练代价函数为频域误差；
• Linear-Lagged，采用线性模型，训练代价函数为长程误差；
• Acceleration-One-Step，采用作者提出的加速度预测模型，训练代价函数为一步误差；
• Acceleration-Lagged，采用加速度预测模型，训练代价函数为长程误差。
  
  
  图6 实验中使用的直升机
  
   为了验证模型，作者先把测试数据划分成连续不重叠的时间窗口，每个窗口为2秒，即包含20个数据。在每个时间窗口上，第一个点都作为起始状态点S0。然后根据所有的窗口的数据得到不同状态的平均平方误差。实验结果如图5所示：
  
  
  图7 实验室结果。蓝色虚线：Linear-One-Step；绿色破折号：Linear-CIFER；黄色三角：Linear-Lagged；红色虚线：LinearLagged使用梯度下降训练的方法；粉红十字：Acceleration-One-Step；青色圆形：Acceleration-Lagged；黑色星形：Acceleration-Lagged使用梯度下降训练的方法

 实验表明Linear-Lagged始终在Linear-CIFER和Linear-One-Step的下方，说明根据长程误差来训练的模型效果最好。同时Acceleration-模型在所有线性模型的下面，这表明基于加速度预测的模型优于线性模型，Acceleration-Lagged在所有曲线的下方更是印证了这一点。

2.4 扑翼动力学模型的假设

 目前我们的扑翼有3个控制输入量，油门量：它控制主电机的转速，平尾舵机：它可以控制飞机平尾的角度，垂尾舵机：它可以控制飞机垂尾的角度，目前飞机没有加上副翼的控制，但是下面的分析还是加入了副翼的控制：

• U1，扑翼平尾舵机的输入量，它能够控制飞机的俯仰角度，根据常识可以知道，俯仰角度不仅和平尾摆动的角度关，还和无人机的前向速度有关。
• U2，扑翼副翼的控制(目前还没有加副翼)，它可以控制飞机的横滚，根据常识可以知道，横滚的角度不仅和副翼的角度有关，还可无人机的前向速度有关。
• U3，扑翼的垂尾控制，它能够控制飞机的偏航角度，根据常识可以知道，偏航的角度不仅和垂尾的角度有关，还和飞机的前向速度有关。
• U4，扑翼主电机的输入量(油门)，他可以控制飞机的扑动频率，不同的扑动频率可以带来不同的升力和推力，我们的经验发现，扑动频率低的情况下，升力相对推力较大，扑动频率高时，升力相对推力较小，因此升力和推力不是线性相关的。同时在不同飞行速度的情况下，相同的油门量对应的扑动频率并不一致，同时由于齿轮滑动的缘故，更加对应不上翅膀的扑动频率了，因此提取扑动频率只能靠竖直方向加速度的分析。
   我们假设扑翼的动力学模型如下：
  
  
  图8 假设的扑翼模型
  
   在式子中，俯仰角加速度由自身带来的阻尼、平尾输入量(平尾的角度)乘于飞机前向的速度、常数项共同决定，同理横滚和偏航也是这样。对于向前的加速度由自身带来的阻尼、重力加速度作用在机身x轴方向的力、翅膀扑动得到的前向的力(通过一个函数计算当前油门的输入量计算得到)、常数项共同决定。同理z轴方向也是这样，但是在y轴上，也就是飞机侧向的力只有阻尼和重力的分量得到。

3 通过强化学习的方法设计一个控制器

3.1 控制器的学习

 假设在一个马尔科夫决策中，S代表状态控制，A代表动作空间，Psa代表状态转移概率分布，R代表奖励函数，γ代表折扣值，π代表执行策略(根据当前状态决定输出动作)。强化学习的目标就是学习到一个策略π最大化下面的值函数：

图9 值函数的计算

 值函数是连续状态下所有奖励值加权的和，同时未来状态的回报是需要乘于γ折扣值的，因为在强化学习中，一般来讲未来的奖励比较难以传递到当前时刻，同时这符合人类更加注重眼前利益的特点。
 一个标准的蒙特卡洛决策过程是这样的：系统在初始状态S0，根据当前状态选择一个动作即里面的动作A0；由于动作的输入，系统根据概率转移函数Psa随机的切换到下一个状态S2，每一个状态的变化可以通过奖赏函数得到一个奖赏值；根据奖赏值优化决策函数，再根据新的决策得到下一时刻应该选择的动作，然后这样周而复始。
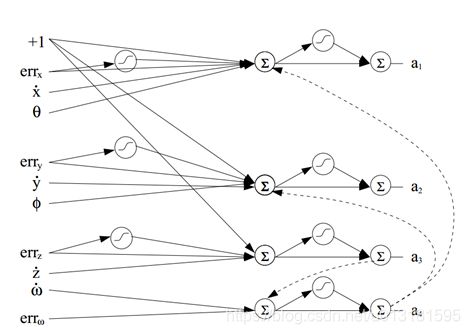
作者先设定了一个悬停的控制任务，假定期望的位置和角度为(x*,y*,z*,w*)，通过当前的状态计算得到合适的输出量，来让飞机稳定在这个位置。为此作者设计了一个简单神经网络的控制器。

图10 神经网络的控制器

 图中的每一条边都代表一个权重，通过简单的推理将一些节点连接起来，比如a1(纵向拉杆的控制，可以认为向前运动的力)通道的输出和X轴坐标的误差、X轴的速度，Pitch角度的大小有关。对于a1输出量的计算如下所示：

图11 a1的计算

 其中w1,2,3,4等是训练过程中需要学习的权重。Errx是X轴的误差，xb是X轴的速度，θ是Pitch角度。
 在神经网络训练的过程中，采用的代价函数为，这里取负号是t时刻的R(s)需要用于计算奖励值：

图12 控制器的代价函数

 其中αx,y,z等等是手动选择的超参数，假如对于X轴的位置误差要求比较严格，可以把αx设置的大一点。同时为了鼓励小范围的输出，使飞机控制的更稳定，作者还加入了一个控制输出的二次项惩罚

图13 输出的二次惩罚

 把两个误差加起来作为总的误差函数。有了代价函数就可以计算得到奖励值了，结合上面飞机的动力模型就可以训练出最佳的策略π。
 在作者较新的论文中对控制器提出了2点改进：

• 对把输出控制的改变量加入奖励函数中，因为作者发现，2次输出变化太剧烈的话会影响飞行性能；
• 在控制器的输入中，加入误差的积分以消除机身或者风带来的静态误差。
  在训练过程中，作者采用梯度上升的办法来最大化奖励值。先采用在数值上对奖励函数求每个权重的偏导，然后对神经网络的权重进行更新。在训练过程中对导数的缩放很重要，因为有时候导数的估计在数值上是不稳定的。

3.2 实验结果

对于定点飞行的实验，人类和代码控制的对比如下所示

图14 定点飞行的实验结果

红线是人类飞行的数据，蓝线是使用强化学习的数据，通过强化学习得到的控制器性能比人类的手动操作好很多。

4 实现直升机的悬停、倒立飞行

1、 采集人类悬停飞行和倒立飞行的数据，根据采集得到的数据拟合出飞机的运动学模型；
2、 设定一个策略(控制器)，并且把上面学习到的模型用在强化学习中。通过强化学习不断的去优化这个策略，使得奖赏值最大化。不同飞行任务的奖赏函数不太一样；
3、 强化学习优化策略的过程可以采用梯度下降的办法，得到控制器中的最优参数；
4、 在实际飞行中，先由人类手动起飞，达到设定点后再切换控制模式，让飞控接管飞机。
作者首先实现的是悬停飞行，悬停飞行任务中的奖赏函数是这样的：

图15 飞行任务的奖赏函数

 当飞行器需要按指定轨迹飞行时，最简单的办法是设定一系列的位置点，到达每个设定的任务点之后切换到下一个任务点。这种方法的奖赏函数需要修改一下。比如在设定点钟，X轴的位置随着时间逐渐增加(向前飞行)，飞机实际的位置不断的朝着设定值飞行，但是这样的话飞机一直处于追赶的状态，原来的奖赏函数就不太适用了。比如设定轨迹是一条直线，飞机也的确沿着这条直线在飞，但是这样的奖赏函数却一直存在误差。作者改进的办法是把设定点之间的误差，改成当前飞机的速度方向与轨迹方向之间的误差。比如当设定轨迹为沿着X轴直线飞行，则轨迹的方向为(x,0,0)，如果当前飞机的飞行速度也为(x,0,0)则与期望一致，如果飞机当前方向为 (沿着水平面45度飞行)，这样和期望轨迹存在误差。
 而对于倒立飞行的实现，无法根据悬停的数据来设置控制器。作者的做法是先让人类实现倒立飞行，拿到数据后训练出飞机倒立的动力学模型，然后使用一样的强化学习的方法设计出倒立飞行的控制器。

 结论：这种方法可以在完全不知道飞行器空气动力学模型的情况下，学习到它的动力学模型，并在仿真器中学习出一个最佳的控制器来控制飞行。
 不仅仅是飞行器，对于任何载具，或者是控制对象，都可以把它当成一个黑箱来研究，并且通过机器学习的方法去拟合出这个模型，而不是通过频域的方法分析出控制对象的传递函数。有了拟合出来的模型，就可以在电脑上做仿真实验，来设计想要的控制器，或者调整控制器的参数，毕竟通过真实物体的响应一步一步调参的过程太繁琐、低效了。