四种排序：选择，插入，冒泡，快速排序原理及其对应的时间、空间复杂度解析

四种排序：选择，插入，冒泡，快速排序原理及其对应的时间空间复杂度

首先，在了解四种排序之前，让我们来了解一下什么是时间复杂度和空间复杂度。

时间复杂度：算法的时间复杂度是一个函数，它定性描述该算法的运行时间。记做T(n)。直白的来说，就是指运行一段代码所需要的时间。

空间复杂度：空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。记做S(n)。同样的，它是指运行一段代码所需要占用的内存大小。

四种排序：
一.冒泡排序：
你见过鱼儿吐泡泡吗？每次吐一串泡泡，最大的泡泡都会冒到水上，然后是下一个，当最后一个泡泡也冒到水面上时，那么一串泡泡也吐完了。
冒泡排序，顾名思义，和吐泡泡是一个原理。
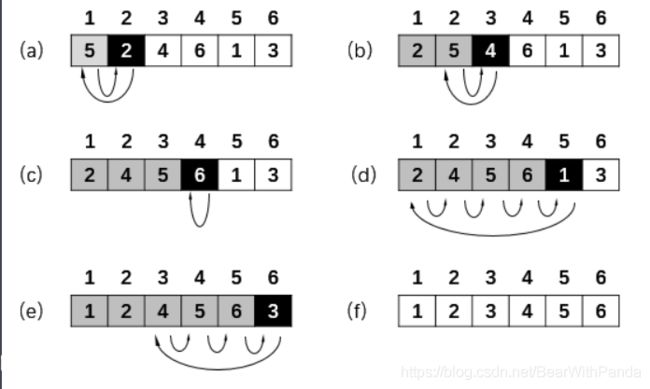
当有一串无需数列待排序时，那么冒泡排序就会每次挑选出最大的数，置于这串数的末尾，然后从剩下的数中再挑选出最大的放置在末尾（这里的末尾应当指当前剩余未排列数组的末尾，即上次排好的数之前）。重复，直到最后一个数被排完。
例： 1 3 5 4 2
要求将这段数升序排列

	那么第一次使用冒泡排序的结果：
	（1 3 ）（3 5)		(5 4)->(4 5)		(5 2)->(2 5)
	1 3 4 2   5
	第二次：
	1 3 2   4 5
	第三次：
	1 2   3 4 5 
	第四次：
	1   2 3 4 5

值得注意的是，如果剩余几个数未进行比较，但是所有的数都已序，那么剩余的数依旧要比较，直到所有的数都比较完。

附上代码：

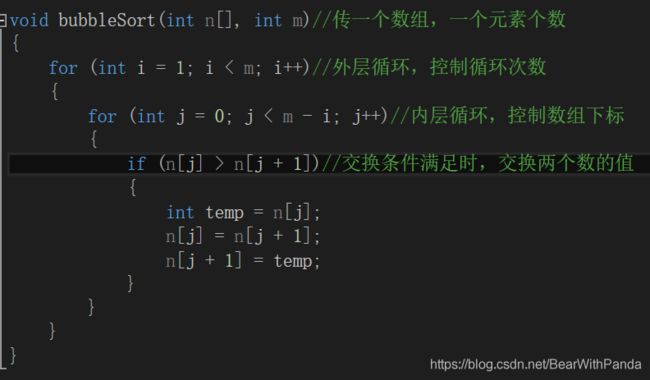
那么，冒泡排序的时间复杂度和空间复杂度各是多少呢？
时间复杂度：

现在我们假设每运行一行代码的时间为t，那么外层循环运行了n-1次，时间为(n-1)t，内层循环运行了n次，时间为nt。
这里，要考虑内层循环的条件判断内容是否执行。
若不出现要交换的次数时
时间最短就为（n-1）+1,时间复杂度为O(n*t)，即O(n)。
若每次都需要交换
时间最长就为(n-1)3nt,时间复杂度为O((3n²-3n)*t)，即O(n²)。
考虑到平均性，我们将以上时间都除以2，那么得到的，就分别是他们的平均时间复杂度。
但是通常情况下，我们认为冒泡排序的时间复杂度为O(n²)。

空间复杂度：

计算空间复杂度时，我们也要分情况考虑。
最优情况为不需要交换，即没有任何临时变量占用空间。
所以空间复杂度为:0;
最坏的情况是全为逆序数，则内层循环每次都要开辟一个temp临时变量的内存，内层循环共n次，即空间复杂度为：O(n)。
平均空间复杂度：O(1)

二.选择排序
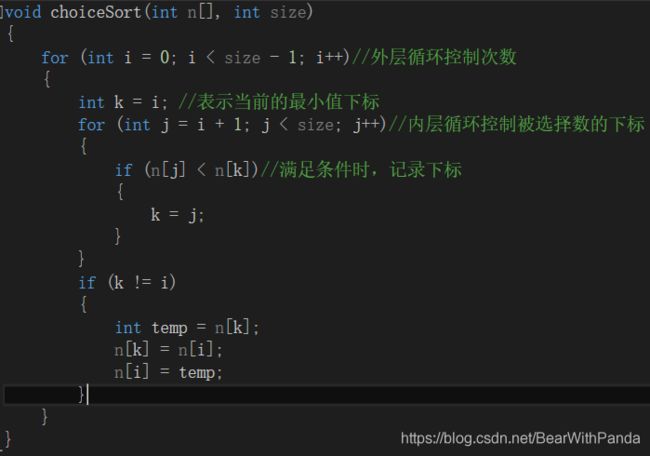
选择排序：即在一组无序数列中，每次选出最大或最小的数，放置在数列的开头，然后继续选出剩下数中最大或最小的数放在已选择数的后面，重复直到最后一个数被选完。

例：1 3 5 2 4
要求将这组数升序排列

那么第一次使用选择排序的结果：
（1 3 ）（1 5) （1 2） （1 4）
1 3 5 2 4
第二次：
1 2 3 5 4
第三次：
1 2 3 5 4
第四次：
1 2 3 4 5

同样的，如果某些数段出现了已序现象，那么依旧要继续遍历完直到最后一个数被选完。

附上代码：

下面我们来计算选择排序的时间复杂度和空间复杂度。
依旧设每个代码执行的时间为t，下同
时间复杂度：
最优情况：当前数列全部已序
那么交换的次数为0次
则时间为(n-1)*t,即最优时间复杂度为O(n)。

最差情况：当前数列全为逆序
那么交换的次数为n-1次
则时间为n*(n-1)*t，即O(n²)。
取平均时间复杂度，则选择排序时间复杂度为O(n²)。

空间复杂度：
最好的情况：不需要交换，
那么空间复杂度为0

最坏的情况：全为逆序数
那么整个过程就需要temp，i，j，k临时变量，即为4
取平均值可以得到选择排序的空间复杂度为O(1)。

三.插入排序
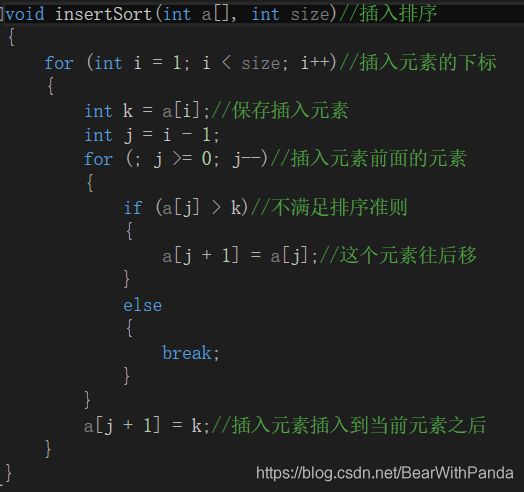
插入排序：插入排序是一种最简单的排序，即在一组无序数列中，将数列分成有序和无序两部分，一般默认第一个数为已序，将第二个数按照排序准则插入已序数列，再将第三个数插入前两个数组成的已序数列，重复。直到最后一个数被插入。

例：1 3 5 2 4
要求将这组数升序排列

那么第一次使用插入排序的结果：
1 3 5 2 4
1 3 5 2 4
第二次：
1 3 5 2 4
1 3 5 2 4
第三次：
1 3 5 2 4
1 2 3 5 4
第四次：
1 2 3 5 4
1 2 3 4 5

依然要注意的是在中途出现已序数段要参与比较。

附上代码：

插入排序的时间复杂度和空间复杂度：
时间复杂度：
最优情况：全为已序数
那么只要比较n-1次，时间为(n-1)*t，
时间复杂度为O(n)；

最坏情况：全为逆序数
那么最多要比较(n-1)*(n-1)/2次
时间复杂度为O(n²)。
平均时间复杂度为O(n²)。

空间复杂度：
最好的情况：全为已序数
无需交换两个数
空间复杂度为0

最坏的情况：全为逆序数
全程需要用到临时变量i j k
所以空间复杂度为O(1)；
插入排序的平均空间复杂度为：O(1)。

四.快速排序
快速排序：快速排序是通过一次分割将一个数列分割成以某个数为界限的左右两部分，一边数小于这个分界值，另一边大于这个分界值。分别再将两遍的数，按照同样的方法各选取一个分界值，分成大于和小于分界值的两部分，依次类推，直到分界值左右部分的数不可再分为止。

例：25 20 30 40 35 50 45
要求将这组数升序排列

任意设定一个分界值：30（但是一般以第一个数为分界值）
那么第一次使用快速排序的结果：
{25 20} 30 {40 35 50 45}
第二次：
再给两边选择分界值
20 {25} 30 {35} 40 {50 45}
此时第一次分界值30左边的部分全部已序，那么下面只要排列右边即可
第三次：
20 {25} 30 {35} 40 {45} 50
到此为止，所有数列全部已序。

要注意的是，当一部分数列已序时，只需要考虑剩余部分即可。
该排序属于一种递归算法。

附上代码：

快速排序的时间复杂度和空间复杂度：
时间复杂度：
最好的情况：
每次划分都将数组平均分：
那么数的个数为（log以2为底2n+1）
第一次要全部遍历，时间为nt
第二次为nt/2
第三次nt/4
……
第n次nt/2的(n减一次方)
则总的T(n)=nT(1)+(log以2为底n)*n
时间复杂度为O(nlog2(n))
即时间复杂度为O(nlogn)。

最坏的情况：
每次选择的分界值只能分出一个子序列，另一个为空。
那么此时需要n-1次递归调用
时间复杂度为O(n²)。

空间复杂度：
最好的情况：每次分割都平均分
所以分割次数为log2(n)
空间复杂度就为O(logn)

最坏的情况：
依旧是每次分割都分割一个子序列和一个空序列。
那么此时需要递归n-1次调用
则空间复杂度为O(n)
快速排序的平均空间复杂度则为O(logn)。