（力扣每日一题）寻宝

寻宝（由于此题用python效率较低主要用java解题）

我们得到了一副藏宝图，藏宝图显示，在一个迷宫中存在着未被世人发现的宝藏。

迷宫是一个二维矩阵，用一个字符串数组表示。它标识了唯一的入口（用 ‘S’ 表示），和唯一的宝藏地点（用 ‘T’ 表示）。但是，宝藏被一些隐蔽的机关保护了起来。在地图上有若干个机关点（用 ‘M’ 表示），只有所有机关均被触发，才可以拿到宝藏。

要保持机关的触发，需要把一个重石放在上面。迷宫中有若干个石堆（用 ‘O’ 表示），每个石堆都有无限个足够触发机关的重石。但是由于石头太重，我们一次只能搬一个石头到指定地点。

迷宫中同样有一些墙壁（用 ‘#’ 表示），我们不能走入墙壁。剩余的都是可随意通行的点（用 ‘.’ 表示）。石堆、机关、起点和终点（无论是否能拿到宝藏）也是可以通行的。

我们每步可以选择向上/向下/向左/向右移动一格，并且不能移出迷宫。搬起石头和放下石头不算步数。那么，从起点开始，我们最少需要多少步才能最后拿到宝藏呢？如果无法拿到宝藏，返回 -1 。

解题思路
1、虽然迷宫有很多格子，但是我们实际上的走法只有几种：
从 S走到 O，我们不会从 S 直接走到 M，因为触发机关要先搬石头
从 O 走到 M
从 M 走到 O
从 M走到 T

2、有一点性质很重要，不论我们触发机关还是搬运石头，都不会改变迷宫的连通状态。因此，两个点的最短距离一旦计算出，就不会再改变了。

3、 于是第一步，我们可以做一步预处理——我们计算所有特殊点（包括 M，O，S，T）互相之间的最短距离，即对这里面的每个点做一次 BFS。

在最开始，我们一定会从 S，经过某一个 O，到达某一个 M。那么对于特定的 M 来说，我们枚举 O 就可以计算 S-O-M 的最短距离。那么如果我们要从起点 S 到达 M，一定会选择这条距离最短的路。这样，我们首先得到了 S 到每一个 M 的最短距离。

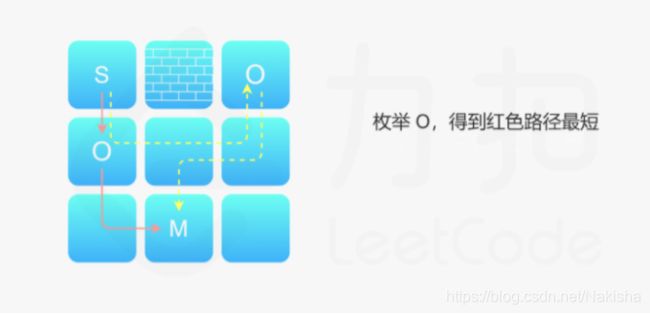
假定我们已经从起点到达了某个 M 了，接下来需要去其他的 O 点搬石头接着触发其他的机关，这是一个 M-O-M′ 的路线。同样的道理，对于给定的 M’，中间的 O 也是固定的。即给定 M 和 M ′，我们可以确定一个 O，使得 M-O-M’距离最短。我们同样可以记录下这个最短距离，即得到了 所有 M 到 M ′的最短距离。

最后，所有 M 到 T 的距离在前面已经计算出了。

代码

class Solution {
    int[] dx = {1, -1, 0, 0};
    int[] dy = {0, 0, 1, -1};
    int n, m;

    public int minimalSteps(String[] maze) {
        n = maze.length;
        m = maze[0].length();
        // 机关 & 石头
        List<int[]> buttons = new ArrayList<int[]>();
        List<int[]> stones = new ArrayList<int[]>();
        // 起点 & 终点
        int sx = -1, sy = -1, tx = -1, ty = -1;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (maze[i].charAt(j) == 'M') {
                    buttons.add(new int[]{i, j});
                }
                if (maze[i].charAt(j) == 'O') {
                    stones.add(new int[]{i, j});
                }
                if (maze[i].charAt(j) == 'S') {
                    sx = i;
                    sy = j;
                }
                if (maze[i].charAt(j) == 'T') {
                    tx = i;
                    ty = j;
                }
            }
        }
        int nb = buttons.size();
        int ns = stones.size();
        int[][] startDist = bfs(sx, sy, maze);

        // 边界情况：没有机关
        if (nb == 0) {
            return startDist[tx][ty];
        }
        // 从某个机关到其他机关 / 起点与终点的最短距离。
        int[][] dist = new int[nb][nb + 2];
        for (int i = 0; i < nb; i++) {
            Arrays.fill(dist[i], -1);
        }
        // 中间结果
        int[][][] dd = new int[nb][][];
        for (int i = 0; i < nb; i++) {
            int[][] d = bfs(buttons.get(i)[0], buttons.get(i)[1], maze);
            dd[i] = d;
            // 从某个点到终点不需要拿石头
            dist[i][nb + 1] = d[tx][ty];
        }

        for (int i = 0; i < nb; i++) {
            int tmp = -1;
            for (int k = 0; k < ns; k++) {
                int midX = stones.get(k)[0], midY = stones.get(k)[1];
                if (dd[i][midX][midY] != -1 && startDist[midX][midY] != -1) {
                    if (tmp == -1 || tmp > dd[i][midX][midY] + startDist[midX][midY]) {
                        tmp = dd[i][midX][midY] + startDist[midX][midY];
                    }
                }
            }
            dist[i][nb] = tmp;
            for (int j = i + 1; j < nb; j++) {
                int mn = -1;
                for (int k = 0; k < ns; k++) {
                    int midX = stones.get(k)[0], midY = stones.get(k)[1];
                    if (dd[i][midX][midY] != -1 && dd[j][midX][midY] != -1) {
                        if (mn == -1 || mn > dd[i][midX][midY] + dd[j][midX][midY]) {
                            mn = dd[i][midX][midY] + dd[j][midX][midY];
                        }
                    }
                }
                dist[i][j] = mn;
                dist[j][i] = mn;
            }
        }

        // 无法达成的情形
        for (int i = 0; i < nb; i++) {
            if (dist[i][nb] == -1 || dist[i][nb + 1] == -1) {
                return -1;
            }
        }
        
        // dp 数组， -1 代表没有遍历到
        int[][] dp = new int[1 << nb][nb];
        for (int i = 0; i < 1 << nb; i++) {
            Arrays.fill(dp[i], -1);
        }
        for (int i = 0; i < nb; i++) {
            dp[1 << i][i] = dist[i][nb];
        }
        
        // 由于更新的状态都比未更新的大，所以直接从小到大遍历即可
        for (int mask = 1; mask < (1 << nb); mask++) {
            for (int i = 0; i < nb; i++) {
                // 当前 dp 是合法的
                if ((mask & (1 << i)) != 0) {
                    for (int j = 0; j < nb; j++) {
                        // j 不在 mask 里
                        if ((mask & (1 << j)) == 0) {
                            int next = mask | (1 << j);
                            if (dp[next][j] == -1 || dp[next][j] > dp[mask][i] + dist[i][j]) {
                                dp[next][j] = dp[mask][i] + dist[i][j];
                            }
                        }
                    }
                }
            }
        }

        int ret = -1;
        int finalMask = (1 << nb) - 1;
        for (int i = 0; i < nb; i++) {
            if (ret == -1 || ret > dp[finalMask][i] + dist[i][nb + 1]) {
                ret = dp[finalMask][i] + dist[i][nb + 1];
            }
        }

        return ret;
    }

    public int[][] bfs(int x, int y, String[] maze) {
        int[][] ret = new int[n][m];
        for (int i = 0; i < n; i++) {
            Arrays.fill(ret[i], -1);
        }
        ret[x][y] = 0;
        Queue<int[]> queue = new LinkedList<int[]>();
        queue.offer(new int[]{x, y});
        while (!queue.isEmpty()) {
            int[] p = queue.poll();
            int curx = p[0], cury = p[1];
            for (int k = 0; k < 4; k++) {
                int nx = curx + dx[k], ny = cury + dy[k];
                if (inBound(nx, ny) && maze[nx].charAt(ny) != '#' && ret[nx][ny] == -1) {
                    ret[nx][ny] = ret[curx][cury] + 1;
                    queue.offer(new int[]{nx, ny});
                }
            }
        }
        return ret;
    }

    public boolean inBound(int x, int y) {
        return x >= 0 && x < n && y >= 0 && y < m;
    }
}