Task4:建模调参
Task4:建模调参
学习自:https://github.com/datawhalechina/team-learning/blob/master/%E6%95%B0%E6%8D%AE%E6%8C%96%E6%8E%98%E5%AE%9E%E8%B7%B5%EF%BC%88%E4%BA%8C%E6%89%8B%E8%BD%A6%E4%BB%B7%E6%A0%BC%E9%A2%84%E6%B5%8B%EF%BC%89/Task4%20%E5%BB%BA%E6%A8%A1%E8%B0%83%E5%8F%82%20.md
学习目标
了解常用的机器学习模型,并掌握机器学习模型的建模与调参流程
学习内容
- 线性回归模型:
- 线性回归对于特征的要求;
- 处理长尾分布;
- 理解线性回归模型;
- 模型性能验证:
- 评价函数与目标函数;
- 交叉验证方法;
- 留一验证方法;
- 针对时间序列问题的验证;
- 绘制学习率曲线;
- 绘制验证曲线;
- 嵌入式特征选择:
- Lasso回归;
- Ridge回归;
- 决策树;
- 模型对比:
- 常用线性模型;
- 常用非线性模型;
- 模型调参:
- 贪心调参方法;
- 网格调参方法;
- 贝叶斯调参方法;
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
def reduce_mem_usage(df):
""" iterate through all the columns of a dataframe and modify the data type
to reduce memory usage.
"""
start_mem = df.memory_usage().sum()
print('Memory usage of dataframe is {:.2f} MB'.format(start_mem))
for col in df.columns:
col_type = df[col].dtype
if col_type != object:
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == 'int':
if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
df[col] = df[col].astype(np.int8)
elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
df[col] = df[col].astype(np.int16)
elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
df[col] = df[col].astype(np.int32)
elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
df[col] = df[col].astype(np.int64)
else:
if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
df[col] = df[col].astype(np.float16)
elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
else:
df[col] = df[col].astype('category')
end_mem = df.memory_usage().sum()
print('Memory usage after optimization is: {:.2f} MB'.format(end_mem))
print('Decreased by {:.1f}%'.format(100 * (start_mem - end_mem) / start_mem))
return df
sample_feature = reduce_mem_usage(pd.read_csv('data_for_tree.csv'))
Memory usage of dataframe is 62099672.00 MB
Memory usage after optimization is: 16520303.00 MB
Decreased by 73.4%
continuous_feature_names = [x for x in sample_feature.columns if x not in ['price','brand','model','brand']]
# 获取训练数据集
sample_feature = sample_feature.dropna().replace('-', 0).reset_index(drop=True)
sample_feature['notRepairedDamage'] = sample_feature['notRepairedDamage'].astype(np.float32)
train = sample_feature[continuous_feature_names + ['price']]
train_X = train[continuous_feature_names]
train_y = train['price']
1. 线性模型
from sklearn.linear_model import LinearRegression
model = LinearRegression(normalize=True)
model = model.fit(train_X, train_y)
# 查看训练的线性回归模型的截距(intercept)与权重(coef)
'intercept:'+ str(model.intercept_)
sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x:x[1], reverse=True)
[('v_6', 3367064.3416418717),
('v_8', 700675.5609399063),
('v_9', 170630.2772322219),
('v_7', 32322.66193203625),
('v_12', 20473.670796956616),
('v_3', 17868.079541493582),
('v_11', 11474.938996702811),
('v_13', 11261.764560014222),
('v_10', 2683.9200905932366),
('gearbox', 881.8225039247454),
('fuelType', 363.90425072159144),
('bodyType', 189.60271012069165),
('city', 44.949751205222555),
('power', 28.553901616746646),
('brand_price_median', 0.5103728134080039),
('brand_price_std', 0.450363470926374),
('brand_amount', 0.1488112039506524),
('brand_price_max', 0.003191018670311645),
('SaleID', 5.355989919856515e-05),
('train', -1.0244548320770264e-07),
('offerType', -2.930755726993084e-07),
('seller', -2.7147470973432064e-06),
('brand_price_sum', -2.175006868187502e-05),
('name', -0.00029800127130996705),
('used_time', -0.0025158943328600102),
('brand_price_average', -0.40490484510127067),
('brand_price_min', -2.246775348689046),
('power_bin', -34.42064411722464),
('v_14', -274.7841180775971),
('kilometer', -372.8975266606936),
('notRepairedDamage', -495.19038446280786),
('v_0', -2045.0549573554758),
('v_5', -11022.98624049396),
('v_4', -15121.731109856253),
('v_2', -26098.299920522953),
('v_1', -45556.18929727541)]
绘制特征v_9的值与标签的散点图,图片发现模型的预测结果(蓝色点)与真实标签(黑色点)的分布差异较大,且部分预测值出现了小于0的情况,说明我们的模型存在一些问题。
为什么要选择v_9?
from matplotlib import pyplot as plt
subsample_index = np.random.randint(low=0, high=len(train_y), size=50)
plt.scatter(train_X['v_9'][subsample_index], train_y[subsample_index], color='black')
plt.scatter(train_X['v_9'][subsample_index], model.predict(train_X.loc[subsample_index]), color='blue')
plt.xlabel('v_9')
plt.ylabel('price')
plt.legend(['True Price','Predicted Price'],loc='upper right')
print('The predicted price is obvious different from true price')
plt.show()
%matplotlib inline
The predicted price is obvious different from true price
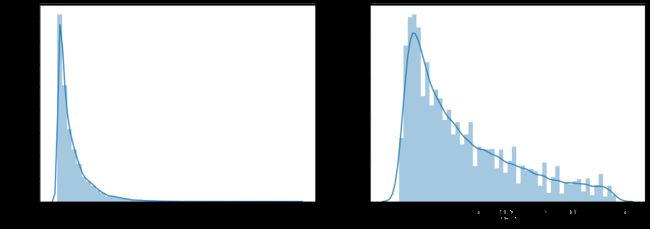
通过作图我们发现数据的标签(price)呈现长尾分布,不利于我们的建模预测。原因是很多模型都假设数据误差项符合正态分布,而长尾分布的数据违背了这一假设。
在使用数据建模时,得看数据是否符合模型的假设。
https://blog.csdn.net/Noob_daniel/article/details/76087829 回归分析的五个基本假设
import seaborn as sns
print('It is clear to see the price shows a typical exponential distribution')
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
sns.distplot(train_y)
plt.subplot(1,2,2)
sns.distplot(train_y[train_y < np.quantile(train_y, 0.9)])
It is clear to see the price shows a typical exponential distribution
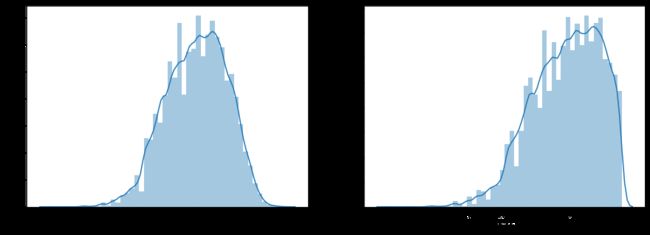
在这里我们对标签进行了 l o g ( x + 1 ) log(x+1) log(x+1) 变换,使标签贴近于正态分布
train_y_ln = np.log(train_y + 1)
import seaborn as sns
print('The transformed price seems like normal distribution')
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
sns.distplot(train_y_ln)
plt.subplot(1,2,2)
sns.distplot(train_y_ln[train_y_ln < np.quantile(train_y_ln, 0.9)])
The transformed price seems like normal distribution
model = model.fit(train_X, train_y_ln)
print('intercept:'+ str(model.intercept_))
sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x:x[1], reverse=True)
intercept:18.7507494655777
[('v_9', 8.05240990056729),
('v_5', 5.764236596650283),
('v_12', 1.6182081236785628),
('v_1', 1.479831058294811),
('v_11', 1.1669016563620904),
('v_13', 0.9404711296031402),
('v_7', 0.7137273083560264),
('v_3', 0.6837875771077782),
('v_0', 0.008500518010120259),
('power_bin', 0.008497969302890544),
('gearbox', 0.007922377278338628),
('fuelType', 0.006684769706828798),
('bodyType', 0.004523520092704174),
('power', 0.0007161894205360409),
('brand_price_min', 3.334351114746047e-05),
('brand_amount', 2.897879704277868e-06),
('brand_price_median', 1.2571172872993166e-06),
('brand_price_std', 6.659176363432616e-07),
('brand_price_max', 6.194956307517354e-07),
('brand_price_average', 5.999345965082222e-07),
('SaleID', 2.1194170039651024e-08),
('seller', 5.696421112588723e-11),
('offerType', 4.128253294766182e-11),
('train', -5.6274984672199935e-12),
('brand_price_sum', -1.5126504215930465e-10),
('name', -7.015512588874946e-08),
('used_time', -4.122479372351641e-06),
('city', -0.0022187824810422163),
('v_14', -0.004234223418102942),
('kilometer', -0.01383586622688452),
('notRepairedDamage', -0.2702794234984635),
('v_4', -0.8315701200993081),
('v_2', -0.9470842241623765),
('v_10', -1.6261466689794903),
('v_8', -40.34300748761742),
('v_6', -238.79036385506777)]
# 再次进行可视化,发现预测结果与真实值较为接近,且未出现异常状况
plt.scatter(train_X['v_9'][subsample_index], train_y[subsample_index], color='black')
plt.scatter(train_X['v_9'][subsample_index], np.exp(model.predict(train_X.loc[subsample_index])), color='blue')
plt.xlabel('v_9')
plt.ylabel('price')
plt.legend(['True Price','Predicted Price'],loc='upper right')
print('The predicted price seems normal after np.log transforming')
plt.show()
The predicted price seems normal after np.log transforming
1.1 五折交叉验证
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_absolute_error, make_scorer
def log_transfer(func):
def wrapper(y, yhat):
result = func(np.log(y), np.nan_to_num(np.log(yhat)))
return result
return wrapper
scores = cross_val_score(model, X=train_X, y=train_y, verbose=1, cv = 5, scoring=make_scorer(log_transfer(mean_absolute_error)))
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 5 out of 5 | elapsed: 0.5s finished
print('AVG:', np.mean(scores))
AVG: 1.3658023920314364
scores = cross_val_score(model, X=train_X, y=train_y_ln, verbose=1, cv = 5, scoring=make_scorer(mean_absolute_error))
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 5 out of 5 | elapsed: 0.5s finished
print('AVG:', np.mean(scores))
AVG: 0.1932530183704744
使用train_y_ln数据相较于train_y数据loss值更小
scores = pd.DataFrame(scores.reshape(1,-1))
scores.columns = ['cv' + str(x) for x in range(1, 6)]
scores.index = ['MAE']
scores
| cv1 | cv2 | cv3 | cv4 | cv5 | |
|---|---|---|---|---|---|
| MAE | 0.190792 | 0.193758 | 0.194132 | 0.191825 | 0.195758 |
1.2 模拟真实情况
时间序列数据的特殊性
但在事实上,由于我们并不具有预知未来的能力,五折交叉验证在某些与时间相关的数据集上反而反映了不真实的情况。通过2018年的二手车价格预测2017年的二手车价格,这显然是不合理的,因此我们还可以采用时间顺序对数据集进行分隔。在本例中,我们选用靠前时间的4/5样本当作训练集,靠后时间的1/5当作验证集,最终结果与五折交叉验证差距不大.
import datetime
sample_feature = sample_feature.reset_index(drop=True)
split_point = len(sample_feature) // 5 * 4
train = sample_feature.loc[:split_point].dropna()
val = sample_feature.loc[split_point:].dropna()
train_X = train[continuous_feature_names]
train_y_ln = np.log(train['price'] + 1)
val_X = val[continuous_feature_names]
val_y_ln = np.log(val['price'] + 1)
model = model.fit(train_X, train_y_ln)
mean_absolute_error(val_y_ln, model.predict(val_X))
0.19577667270301014
from sklearn.model_selection import learning_curve, validation_curve
? learning_curve
# ?查看learning_curve使用
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,n_jobs=1, train_size=np.linspace(.1, 1.0, 5 )):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel('Training example')
plt.ylabel('score')
train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_size, scoring = make_scorer(mean_absolute_error))
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()#区域
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1,
color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color='r',
label="Training score")
plt.plot(train_sizes, test_scores_mean,'o-',color="g",
label="Cross-validation score")
plt.legend(loc="best")
return plt
plot_learning_curve(LinearRegression(), 'Liner_model', train_X[:1000], train_y_ln[:1000], ylim=(0.0, 0.5), cv=5, n_jobs=1)
1.3 多种模型对比
在过滤式和包裹式特征选择方法中,特征选择过程与学习器训练过程有明显的分别。而嵌入式特征选择在学习器训练过程中自动地进行特征选择。嵌入式选择最常用的是L1正则化与L2正则化。在对线性回归模型加入两种正则化方法后,他们分别变成了岭回归与Lasso回归。
在这里,比较这三种模型的效果。
train = sample_feature[continuous_feature_names + ['price']].dropna()
train_X = train[continuous_feature_names]
train_y = train['price']
train_y_ln = np.log(train_y + 1)
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
models = [LinearRegression(),
Ridge(),
Lasso()]
result = dict()
for model in models:
model_name = str(model).split('(')[0]
scores = cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')
LinearRegression is finished
Ridge is finished
Lasso is finished
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result
| LinearRegression | Ridge | Lasso | |
|---|---|---|---|
| cv1 | 0.190792 | 0.194832 | 0.383899 |
| cv2 | 0.193758 | 0.197632 | 0.381893 |
| cv3 | 0.194132 | 0.198123 | 0.384090 |
| cv4 | 0.191825 | 0.195670 | 0.380526 |
| cv5 | 0.195758 | 0.199676 | 0.383611 |
model = LinearRegression().fit(train_X, train_y_ln)
print('intercept:'+ str(model.intercept_))
sns.barplot(abs(model.coef_), continuous_feature_names)
intercept:18.750749465547507
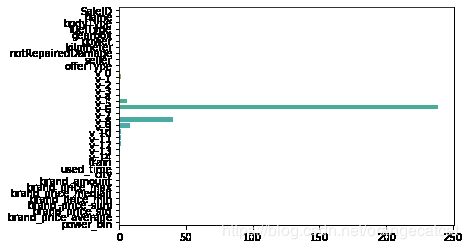
L2正则化在拟合过程中通常都倾向于让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是『抗扰动能力强』
model = Ridge().fit(train_X, train_y_ln)
print('intercept:'+ str(model.intercept_))
sns.barplot(abs(model.coef_), continuous_feature_names)
intercept:4.671709787217615
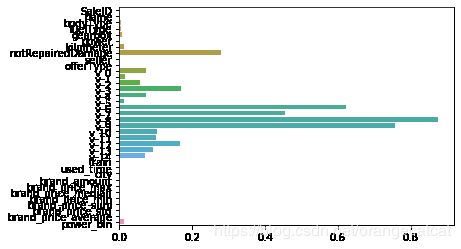
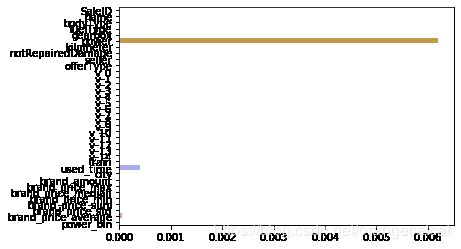
L1正则化有助于生成一个稀疏权值矩阵,进而可以用于特征选择。如下图,我们发现power与userd_time特征非常重要。
model = Lasso().fit(train_X, train_y_ln)
print('intercept:'+ str(model.intercept_))
sns.barplot(abs(model.coef_), continuous_feature_names)
intercept:8.672182462666198
除此之外,决策树通过信息熵或GINI指数选择分裂节点时,优先选择的分裂特征也更加重要,这同样是一种特征选择的方法。XGBoost与LightGBM模型中的model_importance指标正是基于此计算的
2. 非线性模型
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.neural_network import MLPRegressor
from xgboost.sklearn import XGBRegressor
from lightgbm.sklearn import LGBMRegressor
models = [LinearRegression(),
DecisionTreeRegressor(),
RandomForestRegressor(),
GradientBoostingRegressor(),
MLPRegressor(solver='lbfgs', max_iter=100),
XGBRegressor(n_estimators = 100, objective='reg:squarederror'),
LGBMRegressor(n_estimators = 100)]
result = dict()
for model in models:
model_name = str(model).split('(')[0]
scores = cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')
LinearRegression is finished
DecisionTreeRegressor is finished
RandomForestRegressor is finished
GradientBoostingRegressor is finished
MLPRegressor is finished
XGBRegressor is finished
LGBMRegressor is finished
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result
| LinearRegression | DecisionTreeRegressor | RandomForestRegressor | GradientBoostingRegressor | MLPRegressor | XGBRegressor | LGBMRegressor | |
|---|---|---|---|---|---|---|---|
| cv1 | 0.190792 | 0.198480 | 0.141948 | 0.168900 | 485.030894 | 0.142378 | 0.141544 |
| cv2 | 0.193758 | 0.193192 | 0.142863 | 0.171842 | 2296.046816 | 0.140922 | 0.145501 |
| cv3 | 0.194132 | 0.189819 | 0.141740 | 0.170888 | 361.323507 | 0.139393 | 0.143887 |
| cv4 | 0.191825 | 0.191191 | 0.141586 | 0.169076 | 198.310517 | 0.137492 | 0.142497 |
| cv5 | 0.195758 | 0.204885 | 0.145749 | 0.174088 | 3455.657316 | 0.143733 | 0.144852 |
3. 模型调参
常用调参方法
- 贪心算法 https://www.jianshu.com/p/ab89df9759c8
- 网格调参 https://blog.csdn.net/weixin_43172660/article/details/83032029
- 贝叶斯调参 https://blog.csdn.net/linxid/article/details/81189154
## LGB的参数集合:
objective = ['regression', 'regression_l1', 'mape', 'huber', 'fair']
num_leaves = [3,5,10,15,20,40, 55]
max_depth = [3,5,10,15,20,40, 55]
bagging_fraction = []
feature_fraction = []
drop_rate = []
# 贪心调参
best_obj = dict()
for obj in objective:
model = LGBMRegressor(objective=obj)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_obj[obj] = score
best_leaves = dict()
for leaves in num_leaves:
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0], num_leaves=leaves)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_leaves[leaves] = score
best_depth = dict()
for depth in max_depth:
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0],
num_leaves=min(best_leaves.items(), key=lambda x:x[1])[0],
max_depth=depth)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_depth[depth] = score
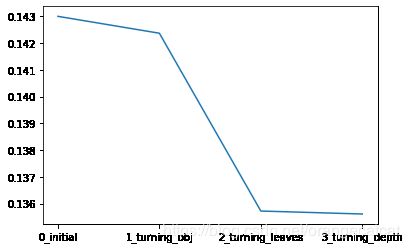
sns.lineplot(x=['0_initial','1_turning_obj','2_turning_leaves','3_turning_depth'], y=[0.143 ,min(best_obj.values()), min(best_leaves.values()), min(best_depth.values())])
# Grid Search 调参
# 这个跑了很久才出结果
from sklearn.model_selection import GridSearchCV
parameters = {'objective': objective , 'num_leaves': num_leaves, 'max_depth': max_depth}
model = LGBMRegressor()
clf = GridSearchCV(model, parameters, cv=5)
clf = clf.fit(train_X, train_y)
clf.best_params_
{'max_depth': 15, 'num_leaves': 55, 'objective': 'regression'}
model = LGBMRegressor(objective='regression',
num_leaves=55,
max_depth=15)
np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
0.13754833106731224
# 贝叶斯调参
from bayes_opt import BayesianOptimization
def rf_cv(num_leaves, max_depth, subsample, min_child_samples):
val = cross_val_score(
LGBMRegressor(objective = 'regression_l1',
num_leaves=int(num_leaves),
max_depth=int(max_depth),
subsample = subsample,
min_child_samples = int(min_child_samples)
),
X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)
).mean()
return 1 - val
rf_bo = BayesianOptimization(
rf_cv,
{
'num_leaves': (2, 100),
'max_depth': (2, 100),
'subsample': (0.1, 1),
'min_child_samples' : (2, 100)
}
)
rf_bo.maximize()
| iter | target | max_depth | min_ch... | num_le... | subsample |
-------------------------------------------------------------------------
| [0m 1 [0m | [0m 0.8686 [0m | [0m 22.73 [0m | [0m 56.37 [0m | [0m 89.36 [0m | [0m 0.2739 [0m |
| [95m 2 [0m | [95m 0.8688 [0m | [95m 79.96 [0m | [95m 40.43 [0m | [95m 96.97 [0m | [95m 0.4042 [0m |
| [0m 3 [0m | [0m 0.8613 [0m | [0m 53.2 [0m | [0m 4.334 [0m | [0m 42.79 [0m | [0m 0.5928 [0m |
| [0m 4 [0m | [0m 0.8655 [0m | [0m 74.97 [0m | [0m 73.88 [0m | [0m 62.97 [0m | [0m 0.3906 [0m |
| [95m 5 [0m | [95m 0.8693 [0m | [95m 48.54 [0m | [95m 37.67 [0m | [95m 99.48 [0m | [95m 0.97 [0m |
| [0m 6 [0m | [0m 0.8503 [0m | [0m 5.72 [0m | [0m 99.79 [0m | [0m 99.58 [0m | [0m 0.1922 [0m |
| [0m 7 [0m | [0m 0.8677 [0m | [0m 51.06 [0m | [0m 59.29 [0m | [0m 79.61 [0m | [0m 0.9962 [0m |
| [0m 8 [0m | [0m 0.7719 [0m | [0m 4.266 [0m | [0m 98.05 [0m | [0m 2.503 [0m | [0m 0.6684 [0m |
| [0m 9 [0m | [0m 0.8119 [0m | [0m 98.12 [0m | [0m 4.939 [0m | [0m 4.031 [0m | [0m 0.3194 [0m |
| [0m 10 [0m | [0m 0.869 [0m | [0m 64.07 [0m | [0m 37.61 [0m | [0m 97.75 [0m | [0m 0.241 [0m |
| [0m 11 [0m | [0m 0.8692 [0m | [0m 98.06 [0m | [0m 98.23 [0m | [0m 97.4 [0m | [0m 0.2644 [0m |
| [0m 12 [0m | [0m 0.8582 [0m | [0m 6.057 [0m | [0m 2.564 [0m | [0m 90.74 [0m | [0m 0.1419 [0m |
| [0m 13 [0m | [0m 0.8678 [0m | [0m 99.08 [0m | [0m 2.514 [0m | [0m 82.52 [0m | [0m 0.4449 [0m |
| [0m 14 [0m | [0m 0.8674 [0m | [0m 99.94 [0m | [0m 44.4 [0m | [0m 75.49 [0m | [0m 0.8095 [0m |
| [0m 15 [0m | [0m 0.8672 [0m | [0m 62.06 [0m | [0m 9.055 [0m | [0m 76.79 [0m | [0m 0.2314 [0m |
| [0m 16 [0m | [0m 0.8689 [0m | [0m 55.33 [0m | [0m 43.65 [0m | [0m 94.94 [0m | [0m 0.1434 [0m |
| [0m 17 [0m | [0m 0.8688 [0m | [0m 54.02 [0m | [0m 40.37 [0m | [0m 93.32 [0m | [0m 0.4546 [0m |
| [0m 18 [0m | [0m 0.8659 [0m | [0m 98.82 [0m | [0m 97.7 [0m | [0m 65.04 [0m | [0m 0.7627 [0m |
| [0m 19 [0m | [0m 0.8689 [0m | [0m 94.74 [0m | [0m 6.816 [0m | [0m 99.66 [0m | [0m 0.1266 [0m |
| [0m 20 [0m | [0m 0.8692 [0m | [0m 99.14 [0m | [0m 66.96 [0m | [0m 98.68 [0m | [0m 0.9479 [0m |
| [0m 21 [0m | [0m 0.8658 [0m | [0m 17.61 [0m | [0m 26.72 [0m | [0m 64.69 [0m | [0m 0.9978 [0m |
| [0m 22 [0m | [0m 0.869 [0m | [0m 68.05 [0m | [0m 99.19 [0m | [0m 95.8 [0m | [0m 0.999 [0m |
| [0m 23 [0m | [0m 0.8684 [0m | [0m 81.45 [0m | [0m 82.26 [0m | [0m 89.57 [0m | [0m 0.1292 [0m |
| [0m 24 [0m | [0m 0.8691 [0m | [0m 58.25 [0m | [0m 73.96 [0m | [0m 99.63 [0m | [0m 0.9913 [0m |
| [95m 25 [0m | [95m 0.8695 [0m | [95m 95.83 [0m | [95m 26.19 [0m | [95m 99.49 [0m | [95m 0.911 [0m |
| [0m 26 [0m | [0m 0.8692 [0m | [0m 95.52 [0m | [0m 98.77 [0m | [0m 98.73 [0m | [0m 0.9349 [0m |
| [0m 27 [0m | [0m 0.869 [0m | [0m 79.8 [0m | [0m 2.675 [0m | [0m 99.26 [0m | [0m 0.9917 [0m |
| [0m 28 [0m | [0m 0.8681 [0m | [0m 93.41 [0m | [0m 87.77 [0m | [0m 87.35 [0m | [0m 0.9969 [0m |
| [0m 29 [0m | [0m 0.869 [0m | [0m 97.98 [0m | [0m 4.108 [0m | [0m 99.81 [0m | [0m 0.84 [0m |
| [0m 30 [0m | [0m 0.8692 [0m | [0m 24.65 [0m | [0m 46.02 [0m | [0m 99.12 [0m | [0m 0.8383 [0m |
=========================================================================
1 - rf_bo.max['target']
0.1305349929845594
plt.figure(figsize=(13,5))
sns.lineplot(x=['0_origin','1_log_transfer','2_L1_&_L2','3_change_model','4_parameter_turning'], y=[1.36 ,0.19, 0.19, 0.14, 0.13])
在本章中,我们完成了建模与调参的工作,并对我们的模型进行了验证。此外,我们还采用了一些基本方法来提高预测的精度,提升如下图所示。