树状数组的区间修改单点查询及Color the ball的AC代码

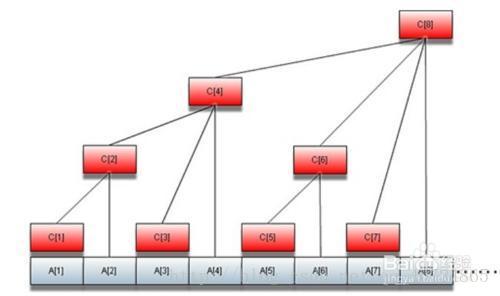
要弄懂树状数组的区间修改，先要熟悉这张图。
细心的你想象将红色快加上重力落到白色快上，你马上发现，哇，原来红白色块的数量相等！
所以你可以把红色快直接当成一列数组，这样就很容易对红色块有了区间的模糊印象
区间不就是a到b中间的那些数吗？只是这红色块的区间有点特别。每一个红色块的值等于它及之前不同数量的白色块值的和。
那么对于白色块而言，每个红色块对应白色块的一个区间，是吧？
事实上，经过一些简单的排列组合，红色块包含了红色块的所有可能区间。
如果我们要将某一区间的所有白色块的值都统一改变某个值，那么在红色块的表现就是，对应白色块区间的那个（些）红色块记录改变的值。
这就叫做区间修改。
如何查询修改后的单点值呢？
举个例子：3包含在[3,3]中，也包含在[2,4]中，…..假如修改的时候，把[1,5]区间加1，把[2,4]区间加2，把[3,3]区间减2，那么我们对区间[3,3]的修改总和就是[1,5]，[2,4]，[3,3]对应的红色块的值之和。注意，修改红色块[2,4]的时候，不会改变[3,3]和[1,5]对应红色块的值，即各个区间都是独立修改的。
因此，对单点值的查询就是，这个点的原值加上包含这个点的所有红色块的值。
如果理解啦以上内容，请继续往下看：

区间修改的实现

我们知道，经典意义下的树状数组的单点修改是这样的：

void UPDATE(int*Tree,int k,int x)
{
    for(int i=k;i>=1;i+=lowbit(i)) Tree[i]+=x;
}

而这里的修改是这样的：

void UPDATE(int*Tree,int k,int x)
{
    for(int i=k;i>=1;i-=lowbit(i)) Tree[i]+=x;//注意这里与单点修改区间查询的唯一区别就是i+=lowbit(x)变成了i-=lowbit(x)
}

加上这个：

        UPDATE(Tree,b,1);
        UPDATE(Tree,a-1,-1);

它们的差别好小，但其实是四两拨千斤。
事实上，在经典意义下，为了维护前缀和，我们改变[3,3]这个红色块时，还要改变所有包含[3,3]的红色块；而这里，我们改变[3,3]这个红色块时就只能改变[3,3]这个红色块，不能改变其他一切红色块。所以我们先改变[3,3]及其之前的红色块，再将其前面的红色块恢复原值，就完成了对且只对[3,3]红色块的修改。

而查询呢？
正好和经典树状数组修改的过程差不多，只要把[3,3]这个红色块和所有包含[3,3]的红色块的值加起来就得到了总的修改。

int SUM(int*Tree,int k)
{
    int sum=0;
    for(int i=k;i<=N;i+=lowbit((i))) sum+=Tree[i];//它和经典意义的修改过程比较类似
    return sum;
}

附加一个小题目：

---

题目很经典，百度即可，注意题中“便为骑上他的…”应该是“便会骑上他的…”

AC代码：

#include 
#include
#include
#include
#include

using namespace std;

#define lowbit(x) x&-x
int N;

void UPDATE(int*Tree,int k,int x)
{
    for(int i=k;i>=1;i-=lowbit(i)) Tree[i]+=x;//注意这里与单点修改区间查询的唯一区别就是i+=lowbit(x)变成了i-=lowbit(x)
}

int SUM(int*Tree,int k)
{
    int sum=0;
    for(int i=k;i<=N;i+=lowbit((i))) sum+=Tree[i];//注意这里也有那个唯一的区别剪号变成了加号
    return sum;
}

void DYE(int*Tree)
{
    int a,b;
    for(int i=1;i<=N;i++)
    {
        scanf("%d%d",&a,&b);
        UPDATE(Tree,b,1);
        UPDATE(Tree,a-1,-1);
    }
}

void OUTPUT(int*Tree)
{
    for(int i=1;iprintf("%d ",SUM(Tree,i));
    printf("%d",SUM(Tree,N));
    printf("\n");
}

int main()
{
    while(scanf("%d",&N)!=EOF && N!=0)
    {
        int*Tree=(int*)malloc(sizeof(int)*(N+2));
        fill(Tree,Tree+(N+2),0);
        DYE(Tree);
        OUTPUT(Tree);
    }
    return 0;
}

有什么问题欢迎留言哦